poj2553 强连通缩点

The Bottom of a Graph

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 10114		Accepted: 4184

Description

We will use the following (standard) definitions from graph theory. Let V be a nonempty and finite set, its elements being called vertices (or nodes). Let E be a subset of the Cartesian product V×V, its elements being called edges. Then G=(V,E) is called a directed graph. 
Let n be a positive integer, and let p=(e₁,...,e_n) be a sequence of length n of edges e_i∈E such that e_i=(v_i,v_i+1) for a sequence of vertices (v₁,...,v_n+1). Then p is called a path from vertex v₁ to vertex v_n+1 in Gand we say that v_n+1 is reachable from v₁, writing (v₁→v_n+1). 
Here are some new definitions. A node v in a graph G=(V,E) is called a sink, if for every node w in G that is reachable from v, v is also reachable from w. The bottom of a graph is the subset of all nodes that are sinks, i.e., bottom(G)={v∈V|∀w∈V:(v→w)⇒(w→v)}. You have to calculate the bottom of certain graphs.

Input

The input contains several test cases, each of which corresponds to a directed graph G. Each test case starts with an integer number v, denoting the number of vertices of G=(V,E), where the vertices will be identified by the integer numbers in the set V={1,...,v}. You may assume that 1<=v<=5000. That is followed by a non-negative integer e and, thereafter, e pairs of vertex identifiers v₁,w₁,...,v_e,w_e with the meaning that (v_i,w_i)∈E. There are no edges other than specified by these pairs. The last test case is followed by a zero.

Output

For each test case output the bottom of the specified graph on a single line. To this end, print the numbers of all nodes that are sinks in sorted order separated by a single space character. If the bottom is empty, print an empty line.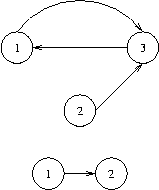

Sample Input

3 3
1 3 2 3 3 1
2 1
1 2
0

Sample Output

1 3
2

题意:

n个点，m条边，并且是单向边。求有多少个顶点，满足它能到的点也能够到达它。

思路:

对于强连通中的点，肯定能够互相到达，所以可以强连通缩点，此时只要找到出度为0的点，其连通分量连所有的点就是答案。因为

如果该点的出度不为0，那么肯定有新的该点能够到达的点，由于已经缩点了，不可能出现有强连通的情况，所以出度不为0的点不满足要求。

/*
 * Author:  sweat123
 * Created Time:  2016/6/25 14:32:24
 * File Name: main.cpp
 */
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<string>
#include<vector>
#include<cstdio>
#include<time.h>
#include<cstring>
#include<iostream>
#include<algorithm>
#define INF 1<<30
#define MOD 1000000007
#define ll long long
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define pi acos(-1.0)
using namespace std;
const int MAXN = 5010;
struct node{
    int from;
    int to;
    int next;  
}edge[MAXN*10];
int pre[MAXN],vis[MAXN],dfn[MAXN],low[MAXN],n,m,ind;
int f[MAXN],siz[MAXN],num,dep,out[MAXN],in[MAXN];
stack<int>s;
vector<int>p[MAXN];
void add(int x,int y){
    edge[ind].from = x;
    edge[ind].to = y;
    edge[ind].next = pre[x];
    pre[x] = ind ++;   
}
void dfs(int rt){
    dfn[rt] = low[rt] = ++dep;
    vis[rt] = 1;
    s.push(rt);
    for(int i = pre[rt]; i != -1; i = edge[i].next){
        int t = edge[i].to;
        if(!dfn[t]){
            dfs(t);
            low[rt] = min(low[rt],low[t]);   
        } else if(vis[t]){
            low[rt] = min(low[rt],dfn[t]);   
        }
    }  
    if(low[rt] == dfn[rt]){
        ++num;
        while(!s.empty()){
            int  tp = s.top();
            s.pop();
            vis[tp] = 0;
            f[tp] = num;
            siz[num] ++;
            p[num].push_back(tp);
            if(tp == rt)break;
        }   
    }
}
void setcc(){
    num = 0;
    dep = 0;
    memset(in,0,sizeof(in));
    memset(out,0,sizeof(out));
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low)); 
    for(int i = 1; i <= n; i++){
        if(!dfn[i]){
            dfs(i);   
        }
    }
    memset(pre,-1,sizeof(pre));
    int ret = ind;
    for(int i = 0; i < ret; i++){
        int x = f[edge[i].from];
        int y = f[edge[i].to];
        if(x == y)continue;
        add(x,y);
        out[x] ++;
        in[y] ++;
    }
    vector<int>ans;
    for(int i = 1; i <= num; i++){
        if(!out[i]){
            for(int j = 0; j < p[i].size(); j++){
                ans.push_back(p[i][j]);   
            }
        }   
    }
    sort(ans.begin(),ans.end());
    for(int i = 0; i < ans.size(); i++){
        if(i == 0)printf("%d",ans[i]);
        else printf(" %d",ans[i]);   
    }
    printf("
");
}
int main(){
    while(~scanf("%d",&n)){
        if(n == 0)break;
        scanf("%d",&m);
        if(n == 1){
            printf("1
");
            continue;   
        }
        ind = 0;
        for(int i = 1; i <= n; i++){
            p[i].clear();   
        }
        memset(pre,-1,sizeof(pre));
        while(!s.empty())s.pop();
        memset(f,-1,sizeof(f));
        memset(siz,0,sizeof(siz));
        for(int i = 1; i <= m; i++){
            int x,y;
            scanf("%d%d",&x,&y);
            add(x,y);
        }   
        setcc();
    }
    return 0;
}

The Bottom of a Graph

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 10114		Accepted: 4184

Description

We will use the following (standard) definitions from graph theory. Let V be a nonempty and finite set, its elements being called vertices (or nodes). Let E be a subset of the Cartesian product V×V, its elements being called edges. Then G=(V,E) is called a directed graph. 
Let n be a positive integer, and let p=(e₁,...,e_n) be a sequence of length n of edges e_i∈E such that e_i=(v_i,v_i+1) for a sequence of vertices (v₁,...,v_n+1). Then p is called a path from vertex v₁ to vertex v_n+1 in Gand we say that v_n+1 is reachable from v₁, writing (v₁→v_n+1). 
Here are some new definitions. A node v in a graph G=(V,E) is called a sink, if for every node w in G that is reachable from v, v is also reachable from w. The bottom of a graph is the subset of all nodes that are sinks, i.e., bottom(G)={v∈V|∀w∈V:(v→w)⇒(w→v)}. You have to calculate the bottom of certain graphs.

Input

The input contains several test cases, each of which corresponds to a directed graph G. Each test case starts with an integer number v, denoting the number of vertices of G=(V,E), where the vertices will be identified by the integer numbers in the set V={1,...,v}. You may assume that 1<=v<=5000. That is followed by a non-negative integer e and, thereafter, e pairs of vertex identifiers v₁,w₁,...,v_e,w_e with the meaning that (v_i,w_i)∈E. There are no edges other than specified by these pairs. The last test case is followed by a zero.

Output

For each test case output the bottom of the specified graph on a single line. To this end, print the numbers of all nodes that are sinks in sorted order separated by a single space character. If the bottom is empty, print an empty line.

Sample Input

3 3
1 3 2 3 3 1
2 1
1 2
0

Sample Output

1 3
2