
1、 翻译——将语言L1转换为逻辑上等价的语言L2
编译——将源程序(高级语言)翻译成目标程序(低级语言或机器语言)
汇编——将低级语言翻译成机器语言
解释(程序)——逐条翻译语句,并立即执行结果
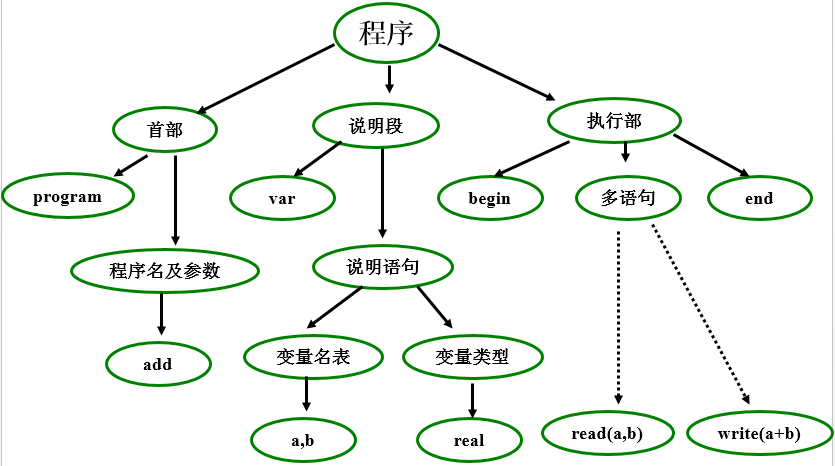
2、 单词——关键字、标识符、常数、界符、运算符
单词 = (单词种别码,单词自身值)
语法单位——短语、表达式、语句、子程序、程序
中间代码——四元式、三元式、逆波兰式、树式

3、 初等数据类型——逻辑、数值、字符、指针
语法:是一组规则,规定了语言的形式结构,包括单词结构,句子结构,程序结构等。
语法={词法规则+句法规则}
语义:也是一组规则,规定了各语法单位的确切含义。
语句
说明性语句——用于定义各种数据类型,变量,函数或过程.
可执行性语句——用于描述数据处理的过程和动作
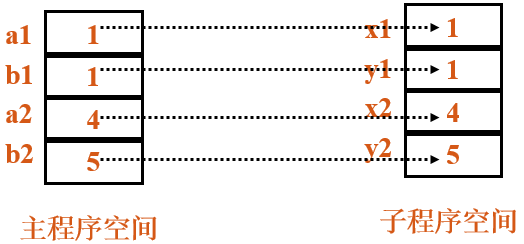
4、 参数传递——传名、传地址、传值

5、正规式
6、状态转换图
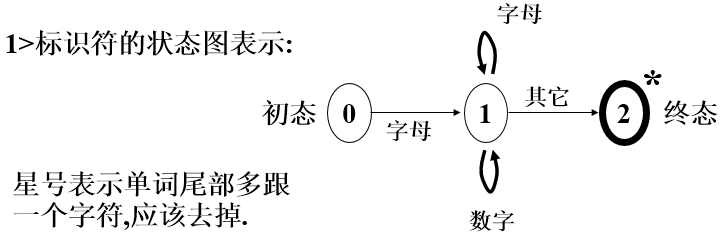

是一有向图,由有限个结点及有向边连接而成;
每个结点称为状态;
状态图有一个初态,多个终态;
每条边上有相应的字符.
状态转换图用于表示单词结构从状态转换图的初态到终态间,每条路径上字符的连接,就构成了该状态图的合法单词.
可以表示单词规则,也可以用于识别单词
由三种结构构成 —— 分支结构、循环结构、终结点
7、 确定有限自动机(DFM)和非确定有限自动机(NFM)
DFAM=(S, ∑, f,s0,Z)
状态集、符号集、单/多值映射函数、初态(1个)、终态集
DFAM 是 NFAM 的特例
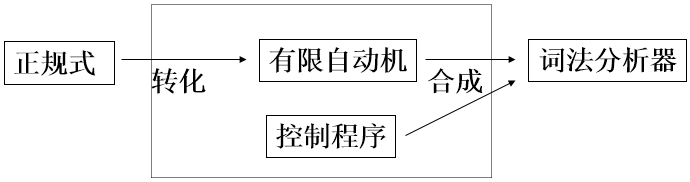
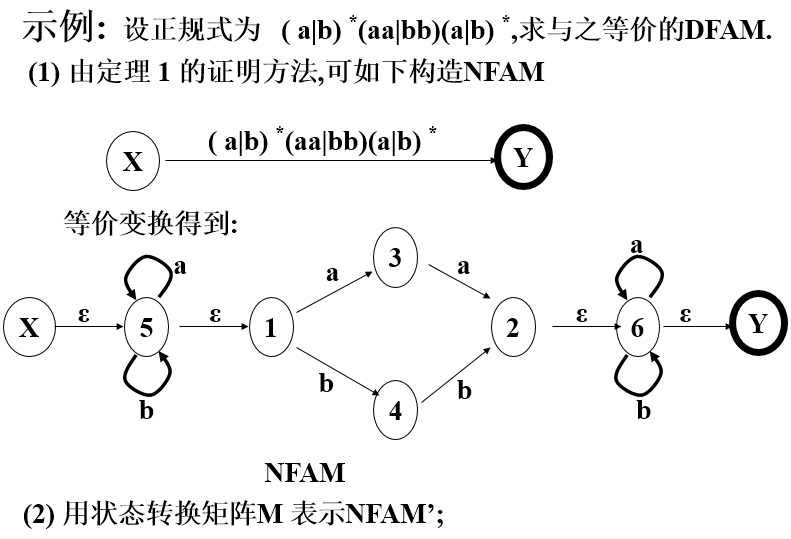
DFAM案例:

NFAM案例:
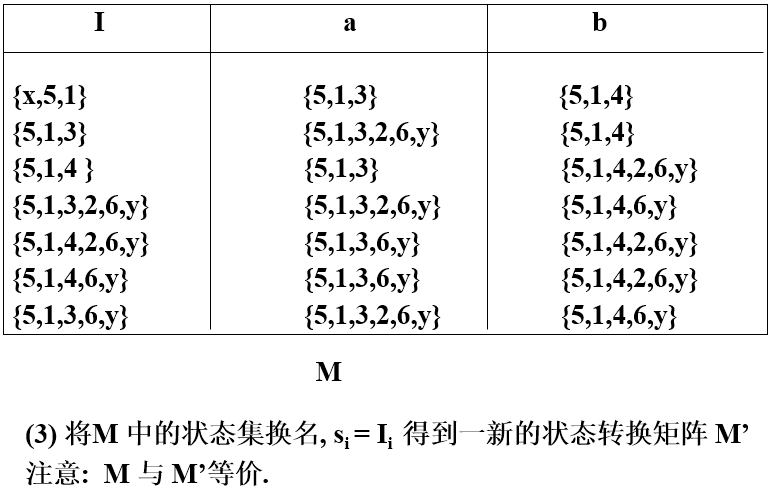

8、 可识别单词的全体记为:L(M)
设 V 为字集,且 V0={ε}, 令 V*=V0∪V1 ∪ V2 ∪........ ,称V* 为V的闭包。 V+= V* - {ε}, 称V+ 为V的正则闭包。
9、 句子——由文法的开始符号出发通过0步或若干步推导产生的终结符号串
若 S=>α,则α ∈VT *
句型——由文法的开始符号出发通过0步或若干步推导产生的符号串
若 S=>α,则α ∈(VT ∪ VN) *
10、语言——所有句子的集合,记为L(G)={α |S=>α, α ∈VT * }
一个语言的文法是不唯一的
11、句柄——一个句型的最左直接短语
简单(直接)短语
短语
素短语——至少含有一个终结点,且除自身外不含有更小的素短语


12、 上下文无关文法——它定义的语法单位独立于该语法单位可能出现的环境
自然语言不是上下文无关文法,程序语言是上下文无关文法
G =(VT,VN,S,P)
终结符集、非终结符集、开始符号、产生式

13、最左推导——每次直接推导,对句型的最左非终结符实行替换
最右推导——每次直接推导,对句型的最右非终结符实行替换
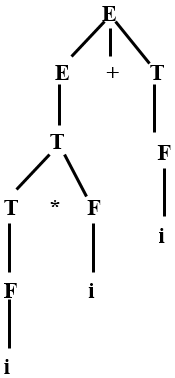
解决语法二义性:E—>i*i+i

14、语法分析方法_自下而上
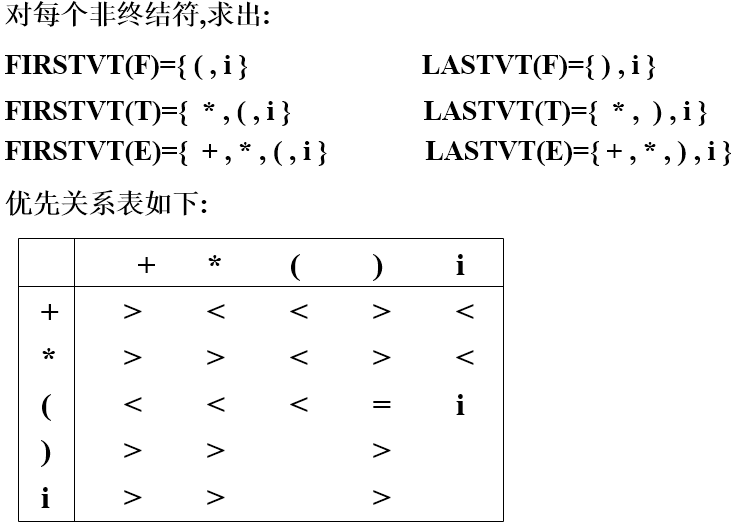
根据文法,对输入字串进行归约,若能正确地归约 为文法的初始符号,则表示输入字串是合法的。典型方法是算符优先分析法。
规范归约(归约栈)——最右推导的逆过程(算符优先分析法)
(1)优先关系表
-
- aQb a=b
- aQ a<FIRSTVT(Q)
- Qb LASTVT(Q)>b
(2)存在的问题
1.文法的左递归
2.文法的回溯
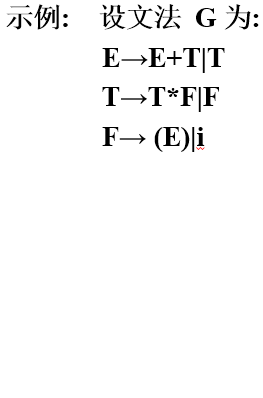
15、语法分析方法_自上而下
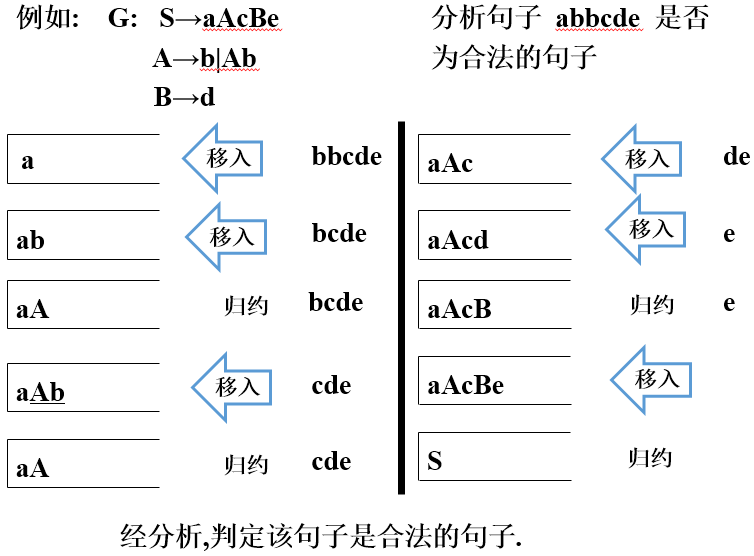
从文法的初始符号进行推导,若能推导出与输入字串相同的句子,则表示输入字串是合法的。 典型方法是递归下降分析法。
规范推导——最左推导的逆过程(递归下降分析法)

16、归约串——栈顶形成的某产生式候选
可归约串(最左素短语)——可正确归约的归约串
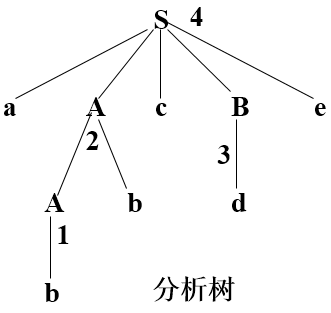
17、语法树 —— 可以表示同一句型的多种推导,是多种推导的共性抽象;但未必代表了同一句型的所有推导
LL(1)文法(无回溯文法)——无二义性、无左递归
LR(0)<SLR(1)<LALR(1)<LR(1)
18、消除左递归
若 P→P α | β ,则 P→ β P ’, P’ → αP ’ | ε
19、 符号表的作用:用于纪录各种名字的信息, 并提供给编译各阶段使用
种属、类型、地址、长度、形参标志、其它信息

20、中间代码的特点: 结构简单,功能明确,易于优化,易于翻译。
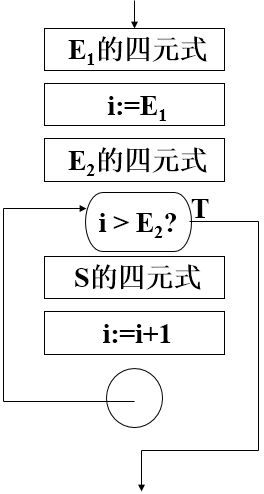
21、语法制导翻译——在语法分析的每次归约或推导时,根据产生式的语义进行翻译的一种方法。
一些基本操作:
- newtemp( ) 产生一临时变量;
- gen(操作符,操作数1,操作数2,结果) 填入四元式表;
- fill( i,属性) 填入符号表;
- entry( i ) 查符号表,返回 i 在符号表中的位置;
- backpatch( m,n) 把 n 填入 四元式表第 m 个四元式中;

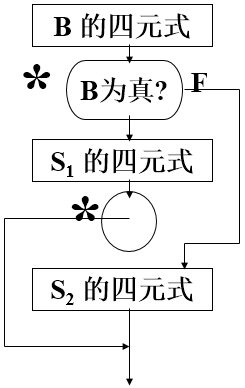


22、语义动作——描述了一定的输入和一定的输出之间的对应关系。
24、基本块——顺序执行的中间代码序列,仅包含一个入口四元式和一个出口四元式。第一条四元式为入口四元式,最后一条四元式为出口四元式,中间部分不含转移四元式。
四元式程序中所有基本入口四元式,包括:
a) 程序的第一条四元式;
b) 转移语句转移到的四元式;
c) 条件语句之后的第一条四元式.
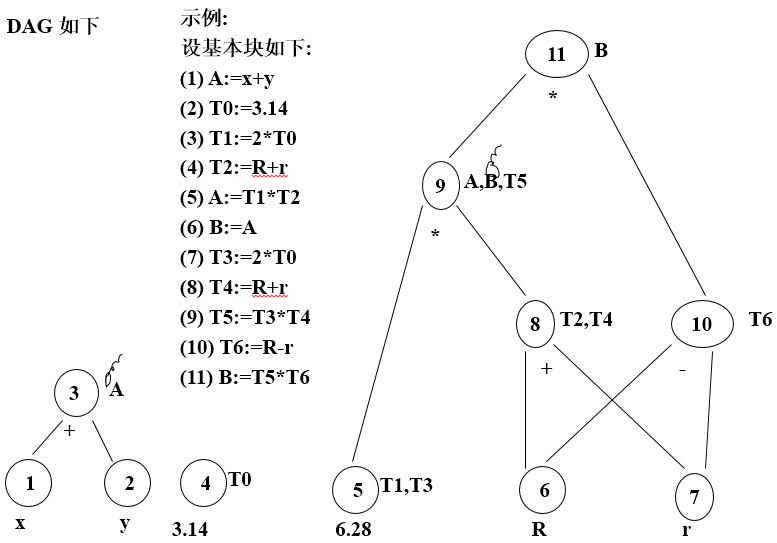
基本块内可以进行以下几种优化:(优化手段: DAG )
合并已知量,删除多余运算(公共子表达式),删除无用赋值。
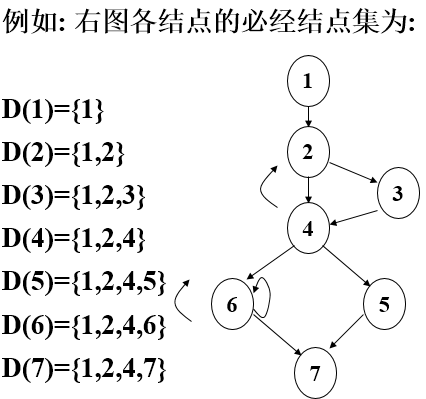
25、回边——若有边b->a且a是b的必经结点,则b->a是回边
控制流程图——具有唯一首结点的有向图,简称为流图
必经结点——从流图首结点出发到达b的通路都必须经过点a,则称a是b的必经结点,记a DOM b
必经结点集——D(n)
26、可归约流图——流图中去除回边后,构成无环路流图
循环——对于回边b->a,包括a、b在内的,有通路到b而不经过a的所有结点构成一个循环
(1) 结点序列为强连通的;(任意两点间都有通路,且通路上的结点都属于结点序列)
(2) 结点序列中仅有一个入口结点.
三种循环优化:代码外提,强度削弱,删除归纳变量。
27、引用--定值集ud[A]
如在 u 处引用了变量 A,则凡能到达 u 的 A 的所有定值点,构成了 A 在 u 处的引用--定值集 ,记为: ud[A].
-
- IN[B] : 代表到达基本块 B 入口点时的各变量的所有定值点集
- OUT[B]:代表到达基本块 B 出口点时的各变量的所有定值点集
- GEN[B]:表示 B 中所定值的且到达 B 之后的定值点集
- KILL[B]: 表示属于 B 外的定值点,而这些定值点所定值的变量,在B中又被重新定值
这几个集合满足如下方程:
-
- OUT[B]=(IN[B] - KILL(B)) ∪ GEN[B]
- IN[B] = OUT[p1] ∪ OUT[p2] ∪...... ∪ OUT[pk]
- p1 , p2...... pk 为B的前趋结点
该方程即为到达--定值方程,求解该方程,得到IN[B]。
28、不变运算——对于循环中的语句 A:= B op C, 若 B 及 C 均为常量,或者为循环中未改变的变量, 那么每次循环 A的值都一样,称A:= B op C为不变运算.
运算对象是常量;
运算对象的定值点均在循环外;
运算对象的再循环内的定值点均已被标记为不变运算;
29、基本归纳变量——若循环中对 B 只有唯一的递归赋值 B:=B+C 且 C 为循环不变量,则称 B 为循环的基本归纳变量
归纳变量——若B为基本归纳变量,而A在循环中的定值可以化归为B的线性函数: A:=C1*B+C2(C1 , C2为循环不变量),则称A 为归纳变量,并称 A与 B同族
待用信息表——指针指向下一个引用的地方
设四元式(i) 对A定值且到达四元式( j) ,四元式 ( j) 中引用 A ,则称 j 是四元式 i 的变量A 的待用信息; 满足上述定义的所有 j, 构成了 A 的待用信息集。
30、目标代码
生成原则:
(1) 生成的目标代码短而高效;
(2) 充分利用寄存器,减少访问内存的次数;
形式:
(1)能立即执行的目标代码;
(2)待装配的浮动目标代码;
(3)汇编语言目标代码;
31、空间分配
