堆排序--leetcode 215

说明

本题可以使用quickSelect，PriorityQueue，或者自己构建堆。

对于要排序的总数是确定的情况下，可以使用quickSelect，对于总数不确定的情况下，可以使用堆排序。

对于前两种方法本文不说明，本文主要说明堆排序。图片来自于这个up

---

堆排序

堆排序要求整棵树是一个完全二叉树（平衡的），它的数组实现方式对空间利用率很高。

堆排序的最佳，平均，最坏时间复杂度都是o(nlogn)的，在平均情况下，它比快速排序慢一个常数因子，但是堆排序更适合外部排序，处理那些数据集太大而不适合在内存中排序的情况。

基于大根堆的排序算法的过程：

• 建堆
• 取出堆顶元素（最大值），放到数组的末尾
• 将堆的最末尾元素放到堆顶，重新构建堆
• 如此重复，直到堆为空

建堆

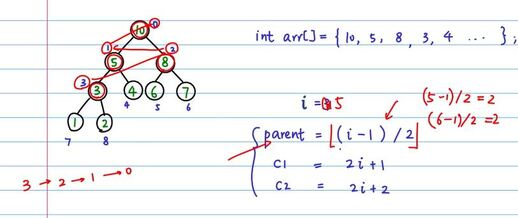
1. 对于数组中index为i的元素的建堆过程是：先判断2i + 1和2i + 2是否越界，如果不越界，找到这两个index中对应的值最大（最大的值的索引记为max）的和i处的值做交换，同时由于交换了索引对应的值，没法保证索引max的子树还是最大堆，所以要对索引max再次建堆（如果都比i处的值小，就不交换）

上述过程对应的代码：

public void heapify(int[] nums, int i, int heapSize){
    int leftChild = 2 * i + 1;
    int rightChild = 2 * i + 2;
    int maxIndex = i;
    if (leftChild < heapSize && nums[leftChild] > nums[maxIndex]){
        maxIndex = leftChild;
    }
    if (rightChild < heapSize && nums[rightChild] > nums[maxIndex]){
        maxIndex = rightChild;
    }

    if (maxIndex != i){
        swap(nums, maxIndex, i);
        heapify(nums, maxIndex, heapSize);
    }
}

public void swap(int[] a, int i, int j) {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
}  

2. 从最后一个非叶子节点往前倒退，分别对这些节点做heapify，就可以构建出整个堆

上述过程的代码：

public void buildMaxHeap(int[] nums, int heapSize){
    for (int i = (heapSize - 1) / 2; i >= 0; i--){
        heapify(nums, i, heapSize);
    }
}

---

取出堆顶元素，放到数组末尾。并将堆末尾元素放到堆顶，重新建堆

执行过程是：交换数组中第一个元素（最大值）和最后一个元素，堆长度-1，对剩下元素重新调整堆。

代码如下：

public int findKthLargest(int[] nums, int k) {
    int heapSize = nums.length;
    buildMaxHeap(nums, heapSize);
    for (int i = nums.length - 1; i >= nums.length - k + 1; i--){
        swap(nums, 0, i);
        heapSize--;
        heapify(nums, 0, heapSize);
    }
    return nums[0];
}

---

总结

本题完整代码如下：

public int findKthLargest(int[] nums, int k) {
    int heapSize = nums.length;
    buildMaxHeap(nums, heapSize);
    for (int i = nums.length - 1; i >= nums.length - k + 1; i--){
        swap(nums, 0, i);
        heapSize--;
        heapify(nums, 0, heapSize);
    }
    return nums[0];
}

public void buildMaxHeap(int[] nums, int heapSize){
    for (int i = (heapSize - 1) / 2; i >= 0; i--){
        heapify(nums, i, heapSize);
    }
}

public void heapify(int[] nums, int i, int heapSize){
    int leftChild = 2 * i + 1;
    int rightChild = 2 * i + 2;
    int maxIndex = i;
    if (leftChild < heapSize && nums[leftChild] > nums[maxIndex]){
        maxIndex = leftChild;
    }
    if (rightChild < heapSize && nums[rightChild] > nums[maxIndex]){
        maxIndex = rightChild;
    }

    if (maxIndex != i){
        swap(nums, maxIndex, i);
        heapify(nums, maxIndex, heapSize);
    }
}

public void swap(int[] a, int i, int j) {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
}

---

补充：堆排序（leetcode 912）

代码如下：

public void heapSort(int[] nums) {
    int heapSize = nums.length;
    buildMaxHeap(nums, heapSize);
    for (int i = nums.length - 1; i >= 0; i--){
        swap(nums, 0, i);
        heapSize--;
        heapify(nums, 0, heapSize);
    }
    
}

public void buildMaxHeap(int[] nums, int heapSize){
    for (int i = (heapSize - 1) / 2; i >= 0; i--){
        heapify(nums, i, heapSize);
    }
}

public void heapify(int[] nums, int i, int heapSize){
    int leftChild = 2 * i + 1;
    int rightChild = 2 * i + 2;
    int maxIndex = i;
    if (leftChild < heapSize && nums[leftChild] > nums[maxIndex]){
        maxIndex = leftChild;
    }
    if (rightChild < heapSize && nums[rightChild] > nums[maxIndex]){
        maxIndex = rightChild;
    }

    if (maxIndex != i){
        swap(nums, maxIndex, i);
        heapify(nums, maxIndex, heapSize);
    }
}

public void swap(int[] a, int i, int j) {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
}


public int[] sortArray(int[] nums) {
    heapSort(nums);
    return nums;
}