hdu1710(Binary Tree Traversals)

Binary Tree Traversals

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2803    Accepted Submission(s): 1242

Problem Description

A binary tree is a finite set of vertices that is either empty or consists of a root r and two disjoint binary trees called the left and right subtrees. There are three most important ways in which the vertices of a binary tree can be systematically traversed or ordered. They are preorder, inorder and postorder. Let T be a binary tree with root r and subtrees T1,T2.

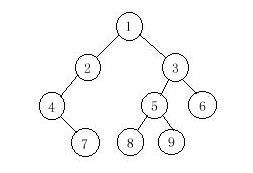
In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.

In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.

In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.

Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.

 

Input

The input contains several test cases. The first line of each test case contains a single integer n (1<=n<=1000), the number of vertices of the binary tree. Followed by two lines, respectively indicating the preorder sequence and inorder sequence. You can assume they are always correspond to a exclusive binary tree.

 

Output

For each test case print a single line specifying the corresponding postorder sequence.

 

Sample Input

9 1 2 4 7 3 5 8 9 6 4 7 2 1 8 5 9 3 6

 

Sample Output

7 4 2 8 9 5 6 3 1

 

Source

HDU 2007-Spring Programming Contest

已知：前序和中序。输出后序

 

#include<cstdio>
#include<iostream>
using namespace std;
struct tree
{
    int num;
    tree *l,*r;
};
int T1[1005],T2[1005];
int n;
void init()
{
    int i;
    for(i=0; i<n; i++)
        scanf("%d",&T1[i]);
    for(i=0; i<n; i++)
        scanf("%d",&T2[i]);
}
int Judge(int x,int y)
{
    int i;
    for(i=0; i<n; i++)
    {
        if(x==T2[i])
            return 1;
        if(y==T2[i])
            return 0;
    }
    return 1;
}

void out(tree *t)//后序遍历
{
    if(t->l)
        out(t->l);
    if(t->r)
        out(t->r);
    T1[n++]=t->num;
}
void BuildTree(tree *&t,int x)//建树
{
    if(t==NULL)
    {
        t=new tree();
        t->num=x;
        t->l=NULL;
        t->r=NULL;
    }
    else
    {
        if(Judge(x,t->num))
        {
            BuildTree(t->l,x);
        }
        else
        {
            BuildTree(t->r,x);
        }
    }
}
void make()
{
    tree *root=NULL;
    int i;
    for(i=0; i<n; i++)
    {
        BuildTree(root,T1[i]);
    }
    n=0;
    out(root);
    for(i=0; i<n-1; i++)
        printf("%d ",T1[i]);
    printf("%d
",T1[i]);
}
int main()
{
    while(scanf("%d",&n)!=EOF)
    {
        init();
        make();
    }
    return 0;
}