题目1: POJ 2318 TOYS
题目大意:
给一个有n个挡板的盒子,从左到右空格编号为0...n。有好多玩具,问每个玩具在哪个空格里面。
算法讨论:
直接叉积判断就可以。注意在盒子的边界上面也算在盒子里面。

1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 #include <iostream> 5 #include <algorithm> 6 #include <cmath> 7 8 using namespace std; 9 10 const int M = 5000 + 5; 11 typedef long long ll; 12 13 int n, m, a, b, c, d; 14 int vi[M], tim = 0, num[M]; 15 16 struct Line { 17 int zx, zy, yx, yy; 18 }l[M]; 19 20 struct Point { 21 int x, y; 22 bool operator < (const Point &h) const { 23 if(h.x == x) return y < h.y; 24 return x < h.x; 25 } 26 }p[M]; 27 28 ll cross(int i, int j) { 29 return 1LL * (l[i].zx - p[j].x) * (l[i].yy - p[j].y) - 1LL * (l[i].yx - p[j].x) * (l[i].zy - p[j].y); 30 } 31 #define ONLINE_JUDGE 32 33 int main() { 34 #ifndef ONLINE_JUDGE 35 freopen("t.txt", "r", stdin); 36 freopen("t.out", "w", stdout); 37 #endif 38 39 int u, v; 40 41 while(scanf("%d", &n) && n) { 42 scanf("%d%d%d%d%d", &m, &a, &b, &c, &d); 43 ++ tim; 44 memset(num, 0, sizeof num); 45 for(int i = 1; i <= n; ++ i) { 46 scanf("%d%d", &u, &v); 47 l[i].zx = u; l[i].zy = b; 48 l[i].yx = v; l[i].yy = d; 49 } 50 l[0].zx = l[0].yx = a; 51 l[0].zy = b; l[0].yy = d; 52 l[n + 1].zx = l[n + 1].yx = c; 53 l[n + 1].zy = b; l[n + 1].yy = d; 54 for(int i = 1; i <= m; ++ i) { 55 scanf("%d%d", &p[i].x, &p[i].y); 56 } 57 for(int i = 0; i < n + 1; ++ i) { 58 for(int j = 1; j <= m; ++ j) { 59 if(vi[j] == tim) continue; 60 if(p[j].y == b) { 61 if(p[j].x >= l[i].zx && p[j].x <= l[i + 1].zx) { 62 vi[j] = tim; 63 num[i] ++; 64 } 65 } 66 else if(p[j].y == d) { 67 if(p[j].x >= l[i].yx && p[j].x <= l[i + 1].yx) { 68 vi[j] = tim; 69 num[i] ++; 70 } 71 } 72 else if(i == 0 && p[j].x == a) { 73 vi[j] = tim; 74 num[0] ++; 75 } 76 else if(i == n && p[j].x == c) { 77 vi[j] = tim; 78 num[n] ++; 79 } 80 else if(1LL * cross(i, j) * cross(i + 1, j) < 0) { 81 vi[j] = tim; 82 num[i] ++; 83 } 84 } 85 } 86 for(int i = 0; i < n + 1; ++ i) { 87 printf("%d: %d ", i, num[i]); 88 } 89 puts(""); 90 } 91 92 #ifndef ONLINE_JUDGE 93 fclose(stdin); fclose(stdout); 94 #endif 95 return 0; 96 }
题目2: POJ 2398 Toys
题目大意:
同上。不过不同的是,这里面的挡板输入是没有顺序的,而且问的是有t个玩具的格子有几个。
算法讨论:
上个题小小变动一下就可以了。

1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 #include <iostream> 5 #include <algorithm> 6 #include <cmath> 7 8 using namespace std; 9 10 const int M = 5000 + 5; 11 typedef long long ll; 12 13 int n, m, a, b, c, d; 14 int vi[M], tim = 0, num[M], out[M]; 15 16 struct Line { 17 int zx, zy, yx, yy; 18 bool operator < (const Line &h) const { 19 int lx1 = max(zx, yx), mx1 = min(zx, yx); 20 int lx2 = max(h.zx, h.yx), mx2 = min(h.zx, h.yx); 21 22 if(mx2 == mx1) { 23 return lx1 < lx2; 24 } 25 return mx1 < mx2; 26 } 27 }l[M]; 28 29 struct Point { 30 int x, y; 31 bool operator < (const Point &h) const { 32 if(h.x == x) return y < h.y; 33 return x < h.x; 34 } 35 }p[M]; 36 37 ll cross(int i, int j) { 38 return 1LL * (l[i].zx - p[j].x) * (l[i].yy - p[j].y) - 1LL * (l[i].yx - p[j].x) * (l[i].zy - p[j].y); 39 } 40 #define ONLINE_JUDGE 41 42 int main() { 43 #ifndef ONLINE_JUDGE 44 freopen("t.txt", "r", stdin); 45 freopen("t.out", "w", stdout); 46 #endif 47 48 int u, v; 49 50 while(scanf("%d", &n) && n) { 51 scanf("%d%d%d%d%d", &m, &a, &b, &c, &d); 52 ++ tim; 53 memset(num, 0, sizeof num); 54 memset(out, 0, sizeof out); 55 for(int i = 1; i <= n; ++ i) { 56 scanf("%d%d", &u, &v); 57 l[i].zx = u; l[i].zy = b; 58 l[i].yx = v; l[i].yy = d; 59 } 60 sort(l + 1, l + n + 1); 61 l[0].zx = l[0].yx = a; 62 l[0].zy = b; l[0].yy = d; 63 l[n + 1].zx = l[n + 1].yx = c; 64 l[n + 1].zy = b; l[n + 1].yy = d; 65 for(int i = 1; i <= m; ++ i) { 66 scanf("%d%d", &p[i].x, &p[i].y); 67 } 68 for(int i = 0; i < n + 1; ++ i) { 69 for(int j = 1; j <= m; ++ j) { 70 if(vi[j] == tim) continue; 71 if(p[j].y == b) { 72 if(p[j].x >= l[i].zx && p[j].x <= l[i + 1].zx) { 73 vi[j] = tim; 74 num[i] ++; 75 } 76 } 77 else if(p[j].y == d) { 78 if(p[j].x >= l[i].yx && p[j].x <= l[i + 1].yx) { 79 vi[j] = tim; 80 num[i] ++; 81 } 82 } 83 else if(i == 0 && p[j].x == a) { 84 vi[j] = tim; 85 num[0] ++; 86 } 87 else if(i == n && p[j].x == c) { 88 vi[j] = tim; 89 num[n] ++; 90 } 91 else if(1LL * cross(i, j) * cross(i + 1, j) < 0) { 92 vi[j] = tim; 93 num[i] ++; 94 } 95 } 96 } 97 for(int i = 0; i < n + 1; ++ i) { 98 out[num[i]] ++; 99 } 100 puts("Box"); 101 for(int i = 1; i <= m; ++ i) { 102 if(out[i]) 103 printf("%d: %d ", i, out[i]); 104 } 105 } 106 107 #ifndef ONLINE_JUDGE 108 fclose(stdin); fclose(stdout); 109 #endif 110 return 0; 111 }
题目3: POJ 1654 Area
题目大意:
给一个数字序列,每个数字都代表向特定的方向走。求数字围成的多边形的面积。数据保证合法。
算法讨论:
直接做就行。注意输出的时候,分类讨论下就可以了。而且注意内存,不能把点存下来,要边读入边计算。

1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 #include <algorithm> 5 #include <iostream> 6 #include <cmath> 7 8 using namespace std; 9 10 const int N = 1000000 + 5; 11 12 int len, cnt; 13 char str[N]; 14 int dx[]={0, 1, 1, 1, 0, 0, 0, -1, -1, -1}; 15 int dy[]={0, -1, 0, 1, -1, 0, 1, -1, 0, 1}; 16 17 double cross(double a, double b, double c, double d) { 18 return a * d - b * c; 19 } 20 21 int main() { 22 int t; 23 24 scanf("%d", &t); 25 26 while(t --) { 27 scanf("%s", str + 1); 28 len = strlen(str + 1); 29 30 double last_x = 0, last_y = 0; 31 double area = 0; 32 33 for(int i = 1; i <= len; ++ i) { 34 int q = str[i] - '0'; 35 36 if(q == 5) { 37 break; 38 } 39 area += cross(last_x, last_y, last_x + dx[q], last_y + dy[q]); 40 last_x += dx[q]; last_y += dy[q]; 41 } 42 43 if((int)area & 1) 44 printf("%.0lf.5 ", floor(fabs(area) / 2)); 45 else 46 printf("%.0lf ", fabs(area) / 2); 47 } 48 return 0; 49 }
题目4: POJ 1269 Intersecting Lines
题目大意:
给出直线对,判断这对直线的关系:平行,重合或者相交。
算法讨论:
假设直线1的两个点编号为1,2,直线2的两个点编号为3,4,如果 1,2,4的叉积为0, 1,2,3的叉积为0,则说明重合。
如果不重合,用两点式算斜率,为了避免除0错误,把两边除法比较变形为乘法。
如果不重合也不平行,就相交,用分点定理找交点。我的代码中只有规范相交的部分。具体代码请见刘汝佳《算法艺术与信息学竞赛》P357页。

1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 #include <algorithm> 5 #include <iostream> 6 #include <cmath> 7 8 using namespace std; 9 10 const double eps = 1e-5; 11 12 int n; 13 14 struct Point { 15 double a, b; 16 Point(double _a = 0, double _b = 0): 17 a(_a), b(_b) {} 18 }c[5]; 19 20 double cross(int i, int j, int k) { 21 return (c[i].a - c[k].a) * (c[j].b - c[k].b) - (c[j].a - c[k].a) * (c[i].b - c[k].b); 22 } 23 24 int dcmp(double s) { 25 return s > eps ? 1 : (s < -eps ? -1 : 0); 26 } 27 28 void solve() { 29 if(fabs(cross(1, 2, 3)) <= eps && fabs(cross(1, 2, 4)) <= eps) puts("LINE"); 30 else if((c[2].b - c[1].b) * (c[4].a - c[3].a) == (c[2].a - c[1].a) * (c[4].b - c[3].b)) 31 puts("NONE"); 32 else { 33 double s1 = cross(1, 2, 3), s2 = cross(1, 2, 4); 34 double x = (c[3].a * s2 - c[4].a * s1) / (s2 - s1); 35 double y = (c[3].b * s2 - c[4].b * s1) / (s2 - s1); 36 37 printf("POINT %.2f %.2f ", x, y); 38 } 39 } 40 41 int main() { 42 double a, b; 43 44 puts("INTERSECTING LINES OUTPUT"); 45 scanf("%d", &n); 46 for(int i = 1; i <= n; ++ i) { 47 for(int j = 1; j <= 4; ++ j) { 48 scanf("%lf%lf", &a, &b); 49 c[j] = Point(a, b); 50 } 51 solve(); 52 } 53 puts("END OF OUTPUT"); 54 return 0; 55 }
题目5: POJ 1113 Wall
题目大意:
求给出点集的凸包长度+一个半径为r的圆的周长和。
算法讨论:
看了下面这个图,你就什么都明白了。
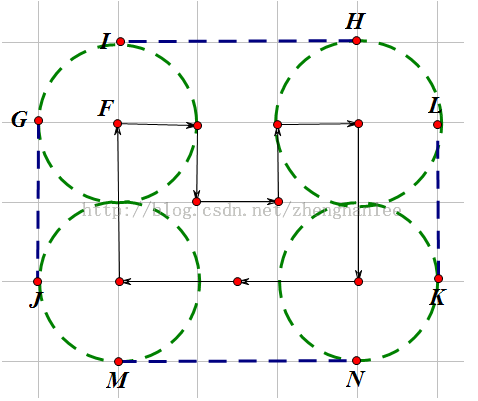

1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 #include <iostream> 5 #include <algorithm> 6 #include <cmath> 7 8 #define pi 3.1415926535 9 10 using namespace std; 11 12 const int N = 1000 + 5; 13 const double eps = 1e-6; 14 15 int n, l; 16 double ans = 0; 17 18 struct Point { 19 double x, y; 20 }p[N], st[N]; 21 22 double dist(Point a, Point b) { 23 return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2)); 24 } 25 26 double cross(Point a, Point b, Point c) { 27 return (a.x - c.x) * (b.y - c.y) - (b.x - c.x) * (a.y - c.y); 28 } 29 30 bool cmp(Point a, Point b) { 31 if(cross(a, b, p[0]) == 0) 32 return dist(a, p[0]) < dist(b, p[0]); 33 return cross(a, b, p[0]) > 0; 34 } 35 36 void Graham() { 37 int top = 2, k = 0; 38 39 for(int i = 1; i < n; ++ i) { 40 if(p[i].x < p[k].x || (p[i].x == p[k].x && p[i].y < p[k].y)) 41 k = i; 42 } 43 swap(p[k], p[0]); 44 sort(p + 1, p + n, cmp); 45 st[0] = p[0]; st[1] = p[1]; st[2] = p[2]; 46 for(int i = 3; i < n; ++ i) { 47 while(top && cross(p[i], st[top], st[top - 1]) >= 0) top --; 48 st[++ top] = p[i]; 49 } 50 st[++ top] = p[0]; 51 for(int i = 0; i < top; ++ i) 52 ans += dist(st[i], st[i + 1]); 53 } 54 55 int main() { 56 scanf("%d%d", &n, &l); 57 for(int i = 0; i < n; ++ i) { 58 scanf("%lf%lf", &p[i].x, &p[i].y); 59 } 60 Graham(); 61 printf("%.0f", (double) ans + (double) 2 * pi * l); 62 return 0; 63 }
题目6: POJ 3304 Segments
题目大意:
给出N个线段,是否有存在一条直线与所有线段都相交。
算法讨论:
这个直线一定经过线段的两个端点。所以我们枚举端点然后判断是否与每条线段相交即可。
判断相交的方法,用跨立实验。如果直线上的两个点与线段的两个点的叉积大于0,说明相交。

1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 #include <iostream> 5 #include <algorithm> 6 #include <cmath> 7 8 using namespace std; 9 10 const int N = 100 + 5; 11 const double eps = 1e-8; 12 13 int n, cnt; 14 15 struct Line { 16 double a, b, c, d; 17 }l[N]; 18 struct Point { 19 double x, y; 20 }p[N<<1]; 21 double cross(int i, int j, int k) { 22 double t1 = (p[i].x - l[k].a) * (p[j].y - l[k].b) - (p[j].x - l[k].a) * (p[i].y - l[k].b); 23 double t2 = (p[i].x - l[k].c) * (p[j].y - l[k].d) - (p[j].x - l[k].c) * (p[i].y - l[k].d); 24 return t1 * t2; 25 } 26 int main() { 27 int t; 28 29 scanf("%d", &t); 30 31 while(t --) { 32 cnt = 0; 33 scanf("%d", &n); 34 for(int i = 1; i <= n; ++ i) { 35 scanf("%lf%lf%lf%lf", &l[i].a, &l[i].b, &l[i].c, &l[i].d); 36 p[++ cnt].x = l[i].a; p[cnt].y = l[i].b; 37 p[++ cnt].x = l[i].c; p[cnt].y = l[i].d; 38 } 39 if(n == 1 || n == 2) { 40 puts("Yes!"); 41 continue; 42 } 43 for(int i = 1; i <= cnt; ++ i) { 44 for(int j = i + 1; j <= cnt; ++ j) { 45 if(fabs(p[i].x - p[j].x) < eps && fabs(p[i].y - p[j].y) < eps) continue; 46 for(int k = 1; k <= n; ++ k) { 47 if(cross(i, j, k) > 0) { 48 break; 49 } 50 if(k == n) { 51 puts("Yes!"); 52 goto A; 53 } 54 } 55 } 56 } 57 puts("No!"); 58 A:; 59 } 60 61 return 0; 62 }
题目7: POJ 2187 Beauty Conteset
题目大意:
求平面点集最远点距离平方。
算法讨论:
旋转卡壳直接上吧。

1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 #include <algorithm> 5 #include <iostream> 6 #include <cmath> 7 8 using namespace std; 9 10 const int N = 50000 + 5; 11 12 int n, top = 2; 13 double ans; 14 15 struct Point { 16 double x, y; 17 }p[N], st[N]; 18 19 double dist(Point a, Point b) { 20 return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2)); 21 } 22 23 double cross(Point a, Point b, Point c) { 24 return (a.x - c.x) * (b.y - c.y) - (b.x - c.x) * (a.y - c.y); 25 } 26 27 double cal(Point a, Point b) { 28 return pow(a.x - b.x, 2) + pow(a.y - b.y, 2); 29 } 30 31 bool cmp(Point a, Point b) { 32 if(cross(a, b, p[0]) == 0) 33 return dist(a, p[0]) < dist(b, p[0]); 34 return cross(a, b, p[0]) > 0; 35 } 36 37 void Graham() { 38 int k = 0; 39 40 for(int i = 1; i < n; ++ i) 41 if(p[i].x < p[k].x || (p[i].x == p[k].x && p[i].y < p[k].y)) 42 k = i; 43 swap(p[0], p[k]); 44 sort(p + 1, p + n, cmp); 45 st[0] = p[0]; st[1] = p[1]; st[2] = p[2]; 46 for(int i = 3; i < n; ++ i) { 47 while(top && cross(p[i], st[top], st[top - 1]) >= 0) top --; 48 st[++ top] = p[i]; 49 } 50 st[++ top] = p[0]; 51 } 52 53 void rotate() { 54 int q = 1; 55 56 for(int i = 0; i < top; ++ i) { 57 while(cross(st[i + 1], st[q + 1], st[i]) > cross(st[i + 1], st[q], st[i])) 58 q = (q + 1) % top; 59 ans = max(ans, max(cal(st[i], st[q]), cal(st[i + 1], st[q + 1]))); 60 } 61 } 62 63 int main() { 64 scanf("%d", &n); 65 for(int i = 0; i < n; ++ i) { 66 scanf("%lf%lf", &p[i].x, &p[i].y); 67 } 68 Graham(); 69 rotate(); 70 printf("%.0f", ans); 71 return 0; 72 }
题目8: POJ 1584 A Round Peg in a Ground Hole
题目大意:
给一个圆和一些点。你要做三件事:判断这些点是否组成一个凸多边形。 圆的圆心是否在多边形内。 圆是否在凸多边形内。
算法讨论:
对于第一个件事,我们直接做Graham然后看有多少个点在凸包上。注意排序的时候,如果三个点在一个竖线上的情况要在cmp函数里面判断一下。
对于第二件事,由于这是一个凸多边形,所以我们用回转角法来判断是否在多边形内。注意这里eps不要取的太小,否则会被卡精度。
对于第三件事,最简单的,直接算距离,注意相切的情况也算在多边形内部。

1 #include <cstdio> 2 #include <iostream> 3 #include <cstring> 4 #include <cstdlib> 5 #include <algorithm> 6 #include <cmath> 7 8 #define pi 3.1415926535 9 10 using namespace std; 11 12 const int N = 100000 + 5; 13 const double eps = 1e-5; 14 15 int n, top = 2; 16 double cx, cy, cr; 17 18 struct Point { 19 double x, y; 20 }p[N], st[N]; 21 22 double dist(Point a, Point b) { 23 return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2)); 24 } 25 26 double cross(Point a, Point b, Point c) { 27 return (a.x - c.x) * (b.y - c.y) - (a.y - c.y) * (b.x - c.x); 28 } 29 30 bool cmp(Point a, Point b) { 31 if(cross(a, b, p[0]) == 0) { 32 if(a.x == b.x && a.x == p[0].x) 33 return dist(a, p[0]) > dist(b, p[0]); 34 else 35 return dist(a, p[0]) < dist(b, p[0]); 36 } 37 return cross(a, b, p[0]) > 0; 38 } 39 40 void Graham() { 41 int k = 0; 42 43 top = 2; 44 for(int i = 1; i < n; ++ i) { 45 if(p[i].x < p[k].x || (p[i].x == p[k].x && p[i].y < p[k].y)) 46 k = i; 47 } 48 swap(p[k], p[0]); 49 sort(p + 1, p + n, cmp); 50 st[0] = p[0]; st[1] = p[1]; st[2] = p[2]; 51 for(int i = 3; i < n; ++ i) { 52 while(top && cross(p[i], st[top], st[top - 1]) > 0) top --; 53 st[++ top] = p[i]; 54 } 55 st[++ top] = p[0]; 56 } 57 58 double len(int i) { 59 return sqrt(pow(st[i].x - cx, 2) + pow(st[i].y - cy, 2)); 60 } 61 62 double cal(int i, int j) { 63 double t1 = (st[i].x - cx) * (st[j].x - cx) + (st[i].y - cy) * (st[j].y - cy); 64 double t2 = len(i) * len(j); 65 66 return t1 / t2; 67 } 68 69 int main() { 70 while(1) { 71 scanf("%d", &n); 72 if(n < 3) break; 73 scanf("%lf%lf%lf", &cr, &cx, &cy); 74 for(int i = 0; i < n; ++ i) { 75 scanf("%lf%lf", &p[i].x, &p[i].y); 76 } 77 Graham(); 78 if(top != n) { 79 puts("HOLE IS ILL-FORMED"); 80 continue; 81 } 82 83 double tmp = 0; 84 bool flag = false; 85 86 for(int i = 0; i < top; ++ i) { 87 tmp += (double)acos(cal(i, i + 1)) * 180 / pi; 88 } 89 if(fabs(tmp - 360.00000) > eps) { 90 puts("PEG WILL NOT FIT"); 91 continue; 92 } 93 for(int i = 0; i < top; ++ i) { 94 tmp = (st[i].x - cx) * (st[i + 1].y - cy) - (st[i + 1].x - cx) * (st[i].y - cy); 95 tmp = fabs(tmp); 96 tmp = tmp / dist(st[i], st[i + 1]); 97 if(tmp - cr < -eps) { 98 flag = true; 99 break; 100 } 101 } 102 if(flag) { 103 puts("PEG WILL NOT FIT"); 104 } 105 else { 106 puts("PEG WILL FIT"); 107 } 108 } 109 return 0; 110 }
题目9: POJ 2079 Triangle
题目大意:
求点集中面积最大的三角形面积。
算法讨论:
类似旋转卡壳的算法。感觉这是个模板题。

1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 #include <iostream> 5 #include <algorithm> 6 #include <cmath> 7 8 using namespace std; 9 10 const int N = 50000 + 5; 11 12 int n, top; 13 double ans = 0; 14 15 struct Point { 16 double x, y; 17 }p[N], st[N]; 18 19 double dist(Point a, Point b) { 20 return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2)); 21 } 22 23 double cross(Point a, Point b, Point c) { 24 return (a.x - c.x) * (b.y - c.y) - (a.y - c.y) * (b.x - c.x); 25 } 26 27 bool cmp(Point a, Point b) { 28 if(cross(a, b, p[0]) == 0) 29 return dist(a, p[0]) < dist(b, p[0]); 30 return cross(a, b, p[0]) > 0; 31 } 32 33 void Graham() { 34 int k = 0; top = 2; 35 36 for(int i = 1; i < n; ++ i) { 37 if(p[i].x < p[k].x || (p[i].x == p[k].x && p[i].y < p[k].y)) 38 k = i; 39 } 40 swap(p[0], p[k]); 41 sort(p + 1, p + n, cmp); 42 st[0] = p[0]; st[1]= p[1]; st[2] = p[2]; 43 for(int i = 3; i < n; ++ i) { 44 while(top && cross(p[i], st[top], st[top - 1]) >= 0)top --; 45 st[++ top] = p[i]; 46 } 47 st[++ top] = p[0]; 48 } 49 50 void rotate_triangle() { 51 int i, j, k, kk; 52 53 for(i = 0; i < top; ++ i) { 54 j = (i + 1) % top; 55 k = (j + 1) % top; 56 while(k != i && cross(st[i], st[j], st[k]) < cross(st[i], st[j], st[k + 1])) 57 k = (k + 1) % top; 58 if(k == i) continue; 59 kk = (k + 1) % top; 60 while(j != kk && k != i) { 61 ans = max(ans, fabs(cross(st[i], st[j], st[k]))); 62 while(k != i && cross(st[i], st[j], st[k]) < cross(st[i], st[j], st[k + 1])) 63 k = (k + 1) % top; 64 j = (j + 1) % top; 65 } 66 } 67 } 68 69 int main() { 70 while(scanf("%d", &n) && n > 0) { 71 ans = 0; 72 for(int i = 0; i < n; ++ i) { 73 scanf("%lf%lf", &p[i].x, &p[i].y); 74 } 75 Graham(); 76 rotate_triangle(); 77 printf("%.2f ", (double) ans / 2); 78 } 79 80 return 0; 81 }
题目10: POJ 2653 Pick-up sticks
题目大意:
给一坨线段,问哪里线段可以被看到。
算法讨论:
在网上看到了两种解法,一个是O(N^2)的暴力,但是不知道为什么对于10W的数据可以跑过。就是枚举每一个线段i,如果有线段和其相交,
那么这个线段就是不可见。
另一个解法就是对于当前线段,判断其是否与队列中的线段有交点,如果有,把有交点的那个线段出队,把这个入队,否则两个一起入队。
看样子是一样的方法啊。我的代码还是没有不规范判断相交的部分。

1 #include <iostream> 2 #include <cstdlib> 3 #include <cstring> 4 #include <algorithm> 5 #include <cstdio> 6 #include <cmath> 7 8 using namespace std; 9 10 const int N = 100000 + 5; 11 const double eps = 1e-6; 12 13 int n; 14 bool flag[N]; 15 16 struct Point { 17 double x, y; 18 Point(double _x = 0, double _y = 0): 19 x(_x), y(_y) {} 20 }; 21 struct Line { 22 Point A, B; 23 }l[N]; 24 25 double cross(Point a, Point b, Point c) { 26 return (a.x - c.x) * (b.y - c.y) - (a.y - c.y) * (b.x - c.x); 27 } 28 29 int dcmp(double x) { 30 return x > eps ? 1 : (x < -eps ? -1 : 0); 31 } 32 33 int segcross(Point a, Point b, Point c, Point d) { 34 int d1, d2, d3, d4; 35 36 d1 = dcmp(cross(a, b, c)); 37 d2 = dcmp(cross(a, b, d)); 38 d3 = dcmp(cross(c, d, a)); 39 d4 = dcmp(cross(c, d, b)); 40 41 if((d1 ^ d2) == -2 && (d3 ^ d4) == -2) 42 return 1; 43 return 0; 44 } 45 46 int main() { 47 double a, b, c, d; 48 49 while(scanf("%d", &n) && n) { 50 for(int i = 1; i <= n; ++ i ) { 51 scanf("%lf%lf%lf%lf", &a, &b, &c, &d); 52 l[i].A = (Point){a, b}; 53 l[i].B = (Point){c, d}; 54 flag[i] = true; 55 } 56 for(int i = 1; i <= n; ++ i) { 57 for(int j = i + 1; j <= n; ++ j) { 58 if(segcross(l[i].A, l[i].B, l[j].A, l[j].B)) { 59 flag[i] = false; 60 break; 61 } 62 } 63 } 64 bool tmp = false; 65 66 printf("Top sticks: "); 67 for(int i = 1; i <= n; ++ i) { 68 if(flag[i]) { 69 if(!tmp) { 70 printf("%d", i); 71 tmp = true; 72 } 73 else { 74 printf(", %d", i); 75 } 76 } 77 } 78 puts("."); 79 } 80 81 return 0; 82 }
