SAT 是适定性(Satisfiability)问题的简称。一般形式为 k - 适定性问题,简称 k-SAT。而当 (k>2) 时该问题为 NP 完全的。所以我们只研究 (k=2) 的情况。
——摘自 OI-Wiki
2-SAT问题大多是固定的模型:
给定若干个均有两个元素的集合,为了方便,我们称集合 (i) 中一个元素为 (A_i) ,另一个元素为 (A_i') 。现在给出若干限制条件,如选择 (A_i) 就不能选择 (A_j) ,选择 (A_i) 就必须选择 (A_j) 等(其中 (i ot= j) )。询问是否存在一种方案,能够在满足限制条件的同时从每一个集合中都选出一个元素。
发现一个限制条件只和两个集合有关,于是我们可以考虑将这种关系抽象成图上的边,将集合中对立的两个元素抽象成点。
若现在有这样一个限制:选择 (A_i) 就不能选择 (A_j) 。那么如果选择 (A_i) 就必须选择 (A_j') ,选择 (A_j) 就必须选择 (A_i') 。对于这样的限制,连边 (A_i o A_j') 和 (A_j o A_i') 。于是图中的边有了具体意义:(u o v) 的边表示若选 (u) 则必选 (v) 。
不难发现,若一个点 (u) 被选择,则 (u) 所能到达的点均必须被选择。这个性质明显与连通性相关。
于是有了一个结论:若一个点 (u) 被选择,那么与 (u) 在同一个强连通分量中的点均必须被选择。
这句话说明同一个强连通分量中的点取或不取的状态是一致的。
这样就能判断是否有解了:若同一个集合中的两个元素在同一个强连通分量中,则问题无解。很显然,若 (A_i) 和 (A_i') 要么同时选,要么都不选,则不满足题设。
求出强连通分量后判断无解:
for(int i=1;i<=n;++i)
if(scc[i]==scc[i+n])
{
puts("IMPOSSIBLE");
return 0;
}
但是有些题不止让你判断有无解,还让你输出可行解,这就需要用到拓扑排序。
设 (S_i) 表示 (A_i) 所在的强连通分量,(S_i') 表示 (A_i') 所在的强连通分量。
推广一下上面对于单点的结论:若一个强连通分量 (S) 被选择,则 (S) 所能到达的强连通分量均必须被选择。
先考虑这样一种情况: (S_i) 与 (S_i') 联通,并且假设 (S_i) 的拓扑序小于 (S_i') 的拓扑序。则必然有:若 (S_i) 被选择,则 (S_i') 必须被选择。那肯定不能选 (S_i) 了,因为 (S_i) 和 (S_i') 必然不能同时选。这样我们就确定了选择方案。
而 (S_i) 与 (S_i') 不连通的话,上面的方法就不行了,因为没法确定选择方案,而一个看起来满足要求的方案可能会对其他的强连通分量产生影响,而枚举方案肯定复杂度爆炸。
我们尝试将两种情况进行统一,即选择 (S_i) 和 (S_i') 中拓扑序大的那个强连通分量。而这样选择其实是正确的,来简单证明一下:
由最初的连边方式可知,得出的图是对称的:
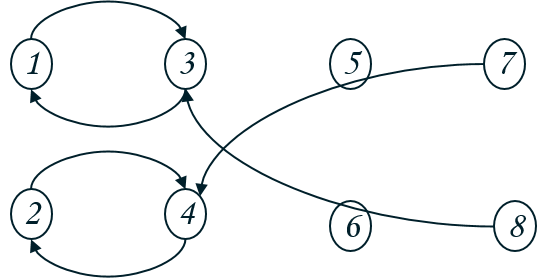
所以缩点后的DAG也是对称的:
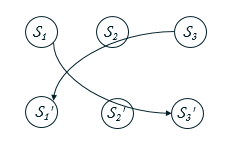
考虑这么一个DAG:
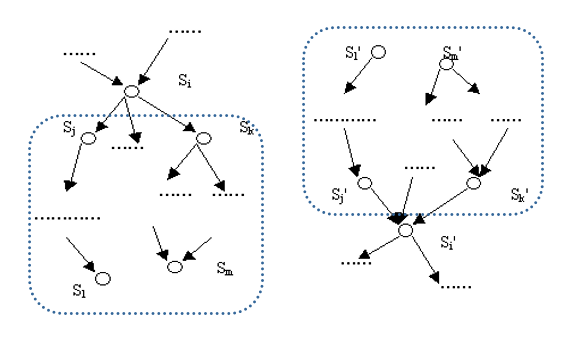
不难看出 (S_i') 的后继结点与 (S_i) 的前驱结点是对称的。
于是选择 (S_i') 会导致 (S_i') 的后继结点全部被选择,而选择 (S_i') 就必须不选 (S_i) ,选择 (S_i') 的后继结点会导致 (S_i) 的前驱结点不被选择。也就是说,(S_i') 以下的结点全选, (S_i) 以上的结点全不选。不难看出,这样选择对虚线框中的结点无影响。
于是可知,这样选择不会导致矛盾。
跑完tarjan后不需要再拓扑,因为tarjan求出的scc编号就是逆拓扑序。
注意一下:若将 (i) 集合拆成 i<<1 和 i<<1|1 两个点,那么从2扫描到n<<1|1 求出的拓扑序对于第二种情况会出锅,大概是因为同一个连通块中结点的拓扑序不连续造成的。
( ext{Code}:)
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <stack>
#define maxn 2000005
#define R register
#define INF 0x3f3f3f3f
using namespace std;
typedef long long lxl;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
struct edge
{
int u,v,next;
}e[maxn];
int head[maxn],k;
inline void add(int u,int v)
{
e[k]=(edge){u,v,head[u]};
head[u]=k++;
}
int n,m,ans[maxn];
int dfn[maxn],low[maxn],dfs_cnt,scc[maxn],scc_cnt;
std::stack<int> S;
bool vis[maxn];
inline void tarjan(int u)
{
S.push(u);
dfn[u]=low[u]=++dfs_cnt;
for(int i=head[u];~i;i=e[i].next)
{
int v=e[i].v;
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(!scc[v]) low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u])
{
++scc_cnt;
int x;
do
{
x=S.top();S.pop();
scc[x]=scc_cnt;
} while (x!=u);
}
}
int main()
{
// freopen("P4782.in","r",stdin);
n=read(),m=read();
memset(head,-1,sizeof(head));
for(int i=1;i<=m;++i)
{
int x=read(),a=read(),y=read(),b=read();
add(x+n*(a&1),y+n*(b^1));
add(y+n*(b&1),x+n*(a^1));
}
for(int i=1;i<=(n<<1);++i)
if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;++i)
if(scc[i]==scc[i+n])
{
puts("IMPOSSIBLE");
return 0;
}
puts("POSSIBLE");
for(int i=1;i<=n;++i)
printf("%d ",scc[i]<scc[i+n]);
return 0;
}
参考文献:国家集训队2003年论文集:伍昱--由对称性解2-SAT问题