题解「CF1000G Two-Paths」

考试做到了类似的一道题 LOJ#6699，题解是换根DP。但是我不会换根，所以用倍增过了这道题qwq。

---

题意

给定一棵树，有点权和边权。询问从 (u) 到 (v)，每条边最多经过两次（即往返两次），经过的点权减边权（点权只算一次）的最大值。

题解

先考虑从点 (u) 开始，进入它的子树再返回所能得到的最大价值。不难想出如下转移方程：

[f(u)=a_u+sum_{v in son_u} { m{max}}{0,f(v)-w(u,v)-w(v,u)} ]

跑一遍树形DP将其计算出来。

然后考虑如何倍增。

记录 $ p(u,i) $ 表示从 (u) 结点向上跳 (2^i) 层后所到达的结点，这可以通过递推的方式求出：

[p(u,i)=p(p(u,i-1),i-1) ]

记录 (F(u,i)) 表示从 (u) 结点到达 (p(u,i)) 或从 (p(u,i)) 到 (u) 所能得到的最大价值（因为这道题在一条边上往返的花费都一样，所以只用记一个数组），也就是说途中可以从路径上的任意一个点进入它的子树再返回。然后我们凭直觉写出这个转移方程：

[F(u,i)=F(u,i-1)+F(p(u,i-1),i-1) ]

但是这样转移，会有一部分信息重复计算，考虑用容斥的思想将这部分剔出去。

(F(u,i-1)) 记录了图中红色区域内的信息，(F(u,i)) 记录了图中蓝色区域内的信息：

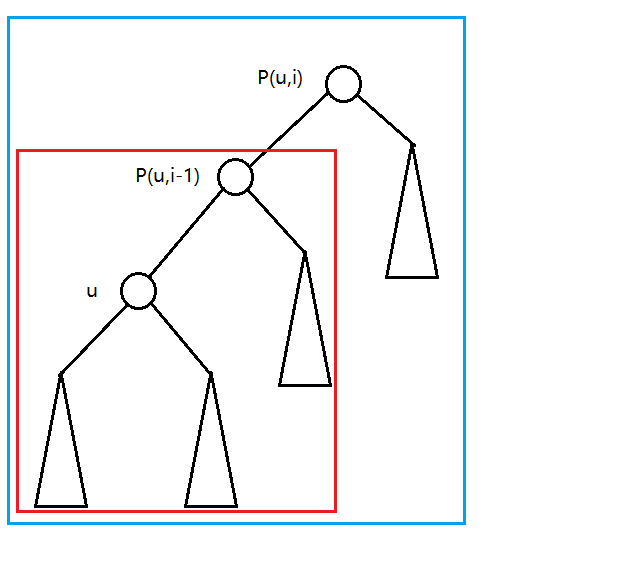
观察一下，缺失的部分正好是 (F(p(u,i-1),i-1)-f(p(u,i-1))) 。于是我们得到了正确的转移方程：

[F(u,i)=F(u,i-1)+F(p(u,i-1),i-1)-f(p(u,i-1)) ]

接着考虑如何统计答案。

由于我们已经把信息记录到了倍增数组 (F) 里面，所以现在只需要进行倍增求LCA的操作，并合并答案。

考虑如何在从 (u) 跳到 (p(u,i)) 时把 (F(u,i)) 拼接到答案中去。

图中红色区域已经统计入答案，蓝色区域是跳到 (p(u,i)) 后统计入答案的区域：

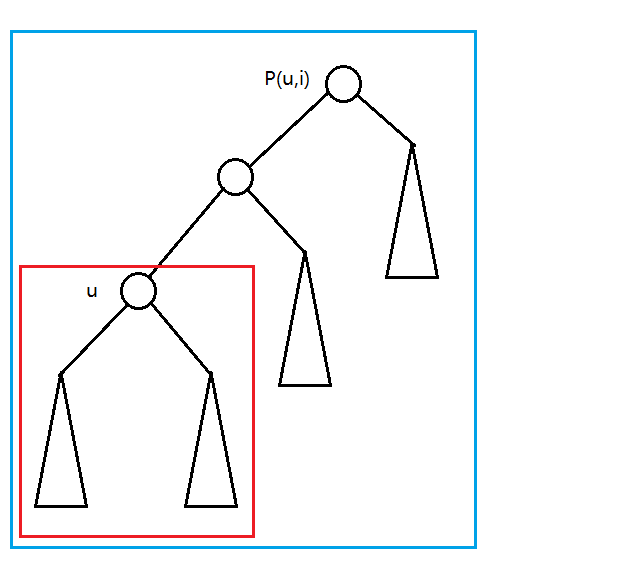
类比上面 (F(u,i)) 的计算过程，发现需要计入答案的就是 (F(u,i)-f(u)) ，边倍增边统计答案即可。

然而当一个结点是另一个结点祖先时，这样统计没什么问题，而当两结点的的LCA不是他们其中任何一个时，在LCA处答案有重复，我们再考虑容斥来解决问题。

当 (u) 与 (v) 都跳到LCA下面时，有下面这个图：

蓝色部分是从 (v) 到 (LCA) 计算入答案的 (LCA) 的其他子树部分，也就是说答案可能包含由 (LCA) 进入蓝色区域的贡献，红色区域同理。绿色区域代表 (f(LCA)) 。

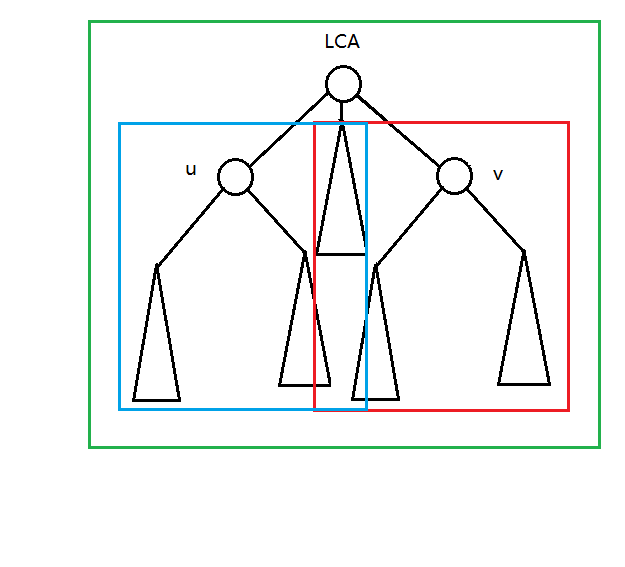
可以发现，(a_{LCA}) 和 (LCA) 除了 (u,v) 的子树信息被计算了两次，而 (LCA) 的子树中 (u,v) 的子树信息不应该统计入答案，多余的信息恰好是 (f(LCA)) ，已经算好了，将这部分在答案中剔除即可。

然后我就这样码了出来，结果样例都过不去。

LCA还可以向它的祖先走，而上面完全没考虑这点，只在子树中统计。

经过乱搞分析，这个信息可以通过它的父亲转移过来，于是再记 (g(u)) 代表从 (u) 向它的祖先走再返回所能得到的最大贡献（注意，这里并没有将 (a_u) 计入 (g(u)) ）。用 (F) 和 (f) 来辅助 (g) 的转移：

[g(u)= { m{max}}{0,g(fa)+F(u,0)-f(u)-w(fa,u)} ]

由于只有 (LCA) 才能向上走，所以最终答案再加上 (g(LCA)) 即可。

---

( ext{Code}:)

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#define maxn 300005
#define R register
#define INF 0x3f3f3f3f
using namespace std;
typedef long long lxl;

inline lxl read()
{
	lxl x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
	return x*f;
}

struct edge
{
	int v,w,next;
}e[maxn<<1];

int head[maxn],k;

inline void add(int u,int v,int w)
{
	e[k]=(edge){v,w,head[u]};
	head[u]=k++;
}

int n,q;
lxl f[maxn],a[maxn];

inline void dp(int u,int fa)
{
	f[u]=a[u];
	for(int i=head[u];~i;i=e[i].next)
	{
		int v=e[i].v;
		if(v==fa) continue;
		dp(v,u);
		if(f[v]-e[i].w-e[i^1].w>0)// 若为负则一定不会进入这棵子树，因为这样会让答案更劣
            f[u]+=f[v]-e[i].w-e[i^1].w;
	}
}

int p[maxn][30];
lxl F[maxn][30],g[maxn];
int dep[maxn];

inline void dfs(int u,int fa)
{
	dep[u]=dep[p[u][0]=fa]+1;
	for(int i=1;i<=25;++i)
	{
		p[u][i]=p[p[u][i-1]][i-1];
		F[u][i]=F[u][i-1]+F[p[u][i-1]][i-1]-f[p[u][i-1]];
	}
	for(int i=head[u];~i;i=e[i].next)
	{
		int v=e[i].v;
		if(v==fa) continue;
		F[v][0]=f[v]+f[u]-e[i^1].w;
		if(f[v]-2*e[i].w>0) F[v][0]-=f[v]-e[i].w-e[i^1].w;// 如果f[u]中包含了f[v]，则将其除去，避免重复计算
		g[v]=max(g[v],g[u]+F[v][0]-e[i].w-f[v]);
		dfs(v,u);
	}
}

inline lxl Query(int u,int v)// 倍增
{
	lxl ans=0;
	int a=u,b=v;
	if(dep[v]>dep[u]) swap(u,v);// 从深度深的开始跳
	for(int i=25;i>=0;--i)
		if(dep[p[u][i]]>=dep[v])
		{
			ans+=F[u][i]-f[u];
			u=p[u][i];
		}
	if(u==v) return ans+((dep[a]>dep[b])?f[a]:f[b])+g[u];
	for(int i=25;i>=0;--i)
		if(p[u][i]!=p[v][i])
		{
			ans+=F[u][i]-f[u]+F[v][i]-f[v];
			u=p[u][i];v=p[v][i];
		}
	return ans+F[u][0]-f[u]+F[v][0]-f[v]-f[p[u][0]]+f[a]+f[b]+g[p[u][0]];
}

int main()
{
	// freopen("CF1000G.in","r",stdin);
	n=read(),q=read();
	for(int i=1;i<=n;++i)
		a[i]=read();
	memset(head,-1,sizeof(int)*(n+5));
	for(int i=1;i<n;++i)
	{
		int u=read(),v=read();
		lxl w=read();
		add(u,v,w);
		add(v,u,w);
	}
	dp(1,0);//计算 f
	dfs(1,0);// 倍增预处理
	while(q--)
	{
		int u=read(),v=read();
		printf("%lld
",Query(u,v));
	}
	return 0;
}