Problem Description:

As a unicorn, the ability of using magic is the distinguishing feature among other kind of pony. Being familiar with composition and decomposition is the fundamental course for a young unicorn. Twilight Sparkle is interested in the decomposition of permutations. A permutation of a set S = {1, 2, ..., n} is a bijection from S to itself. In the great magician —— Cauchy's two-line notation, one lists the elements of set S in the first row, and then for each element, writes its image under the permutation below it in the second row. For instance, a permutation of set {1, 2, 3, 4, 5} σ can be written as:

Here σ(1) = 2, σ(2) = 5, σ(3) = 4, σ(4) = 3, and σ(5) = 1.
Twilight Sparkle is going to decompose the permutation into some disjoint cycles. For instance, the above permutation can be rewritten as:
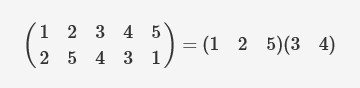
Help Twilight Sparkle find the lexicographic smallest solution. (Only considering numbers).
Input:
Input contains multiple test cases (less than 10). For each test case, the first line contains one number n (1<=n<=10^5). The second line contains n numbers which the i-th of them(start from 1) is σ(i).
Output:
For each case, output the corresponding result.
Sample Input:
5
2 5 4 3 1
3
1 2 3
Sample Output:
(1 2 5)(3 4)
(1)(2)(3)
题意:给出一个序列a,得到一种映射,i<—>a[i],现在问这个映射里面最少有多少个不相交的循环周期(按照字典序输出,但是每个循环周期里不可以排序,按照原序输出)。
#include<stdio.h> #include<string.h> const int N=1e5+10; int a[N], vis[N]; int main () { int n, i, x, pre; while (scanf("%d", &n) != EOF) { memset(vis, 0, sizeof(vis)); ///标记数i是否被输出 for (i = 1; i <= n; i++) scanf("%d", &a[i]); for (i = 1; i <= n; i++) { if (vis[i]) continue; pre = x = i; vis[i] = 1; printf("(%d", i); while (a[x] != pre) ///一直查找到相同时停止,代表找到起始数终止数相等,找到一个循环周期 { printf(" %d", a[x]); x = a[x]; vis[x] = 1; } printf(")"); } printf(" "); } return 0; }