题目:
给一个n个点m条边(2≤m≤100000, 1≤m≤200000)的无向图,每条边上都涂有一种颜色(用1到1000000000表示)。求从结点1到结点n的一条路径,
使得经过的边数尽量少,在此前提下,经过边的颜色序列的字典序最小。一对结点间可能有多条边,一条边可能连接两个相同结点。输入保证结点1可以
到达结点n。
思路:
看到边数尽量少,颜色序列字典序最小,知道这是用BFS来做这个题。但是一直卡在怎么处理颜色的字典序最小上。看了答案之后知道先逆向处理每个节点到终点
的距离d[ i ],然后在正向分层BFS找出颜色最小的一条路径。
1.逆向处理距离d[]数组。
2.正向分层BFS根据当前结点的d[i]与下一个结点的d[i+1]之间差1来得出颜色字典序最小的一条路径。
这里我一开始使用队列来写的,但是这种写法在一层中找最小的颜色的时候是只找了一个结点,这就导致了得出的答案中的颜色不一定是同一条路径上的。
例如下面这个例子:
6 6
1 2 1
1 3 1
2 4 3
3 5 2
4 6 4
5 6 5
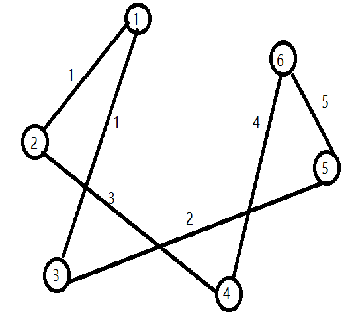
正确的答案应该是1,2,5,而我写出的答案却是1,2,4,苦思无果到网上看了下大佬的博客自己才写出来。
既然是分层BFS那么这种情况我们可以用循环遍历每一层,在每一层中用一个vector数组来存一下这一层中的所有的节点,
在这些节点中查找最小的颜色,然后处理这个最小颜色下面的边连接的点,更新这个vector数组知道结束。
代码:
#include <bits/stdc++.h> #define inf 0x3f3f3f3f #define MAX 1000000009 #define FRE() freopen("in.txt","r",stdin) #define FRO() freopen("out.txt","w",stdout) using namespace std; typedef long long ll; const int maxn = 200010; int n,m,d[maxn],vis[maxn]; struct Edge { int to,color; Edge(int to,int color) { this->to = to; this->color = color; } }; vector<Edge>mp[maxn]; void BFS_reverse() {//逆向简单的BFS求最短路径。各个边的权值为1 memset(vis,0,sizeof(vis)); d[n] = 0; vis[n] = 1; queue<int> que; que.push(n); while(!que.empty()) { int u = que.front(); que.pop(); for(int i = 0; i<mp[u].size(); i++) { Edge e = mp[u][i]; if(vis[e.to]==0) { vis[e.to] = 1; d[e.to] = d[u]+1; que.push(e.to); } } } } void BFS() { memset(vis,0,sizeof(vis)); vector<int> next; next.push_back(1); vector<int> ans; for(int k = 0; k<d[1]; k++) {//遍历这个图中所有的层次 int mmin = MAX; for(int i=0; i<next.size(); i++) {//从这一层中的所有的节点中找到最小的颜色 int u = next[i]; for(int j=0; j<mp[u].size(); j++) { Edge e = mp[u][j]; if(d[e.to]+1==d[u]) { mmin = min(mmin, e.color); } } } ans.push_back(mmin);//将答案颜色保存 vector<int> temp; for(int i=0; i<next.size(); i++) {//保存与最小颜色连接且处于下一层的结点 int u = next[i]; for(int j=0; j<mp[u].size(); j++) { Edge e = mp[u][j]; if(d[u]==d[e.to]+1 && vis[e.to]==0 && e.color==mmin) { temp.push_back(e.to); vis[e.to] = 1; } } } next = temp;//更新next数组 } printf("%d ",ans.size()); printf("%d",ans[0]); for(int i=1; i<ans.size(); i++) { printf(" %d",ans[i]); } printf(" "); return; } int main() { //FRE(); //FRO(); while(scanf("%d%d",&n,&m)!=EOF) { memset(d,0,sizeof(d)); for(int i=0; i<2*n; i++) {//一定要注意这里的范围,一晚上找错误就卡死在这里了 mp[i].clear(); } for(int i = 0; i<m; i++) { int st,en,color; scanf("%d%d%d",&st,&en,&color); mp[st].push_back(Edge(en,color)); mp[en].push_back(Edge(st,color)); } BFS_reverse(); BFS(); } return 0; }