HDU

题目：

　　A clique is a complete graph, in which there is an edge between every pair of the vertices. Given a graph with N vertices and M edges, your task is to count the number of cliques with a specific size S in the graph.

Input：

　　The first line is the number of test cases. For each test case, the first line contains 3 integers N,M and S (N ≤ 100,M ≤ 1000,2 ≤ S ≤ 10), each of the following M lines contains 2 integers u and v (1 ≤ u < v ≤ N), which means there is an edge between vertices u and v. It is guaranteed that the maximum degree of the vertices is no larger than 20.

Output：

　　For each test case, output the number of cliques with size S in the graph.

题意：

　　给出一个图有n个点、m条边，给出子图的大小s，要求求出子图是一个完全图，而且图中需要有s个点。

PS：

我竟然把这个题目读成了求图中点数为s的环的个数，这个锅背的很强，，，，

首先回顾一下完全图的性质：完全图中任意一个点与其他的所有的点都有连边。如下：

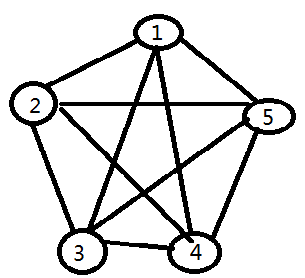
所以有n个点的完全图会有n*（n-1）/2条边。

思路：这个题如果双向建图，然后遍历求点数为s的完全图，铁定TLE，因为同一个图会被多次搜索。要避免重复搜索，可以单向建图，从小到大dfs遍历，同时在path数组中记录已经在完全图中的点，只要当前的点和之前path中的点都有边（这样path中所有的点才能构成完全图），就将该点记录到path中，点数达到s，答案ans++。

代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <map>
#include <set>
#include <vector>
using namespace std;
const int maxn = 100+10;
int m,n,s,ans;
int mp[maxn][maxn];
int path[maxn];
vector<int> G[maxn];

int read()
{
    int res = 0;
    char op = getchar();
    if(op>='0' && op<='9')
    {
        res = op-'0';
        op = getchar();
    }
    while(op>='0' && op<='9')
    {
        res = res*10 + op-'0';
        op = getchar();
    }
    return res;
}


void init()
{
    ans = 0;
    memset(mp,0,sizeof(mp));
    memset(path,0,sizeof(path));
    for(int i = 0; i<maxn; i++)
        G[i].clear();
}

void dfs(int i,int cnt)
{
    if(cnt == s)
    {
        ans++;
        return;
    }
    for(int j = 0; j<G[i].size(); j++)
    {
        int u = G[i][j],f = 0;
        for(int k = 1; k<=cnt; k++)//看点u是否和path中的点是否都有边相连
        {
            if(mp[u][path[k]] == 0)
            {
                f = 1;
                break;
            }
        }
        if(!f)//都想连就存入path继续遍历
        {
            path[cnt+1] = u;
            dfs(u, cnt+1);
            path[cnt+1] = 0;
        }
    }
}


int main()
{
    int T;
    T = read();
    //scanf("%d",&T);
    while(T--)
    {
        init();
        n = read(),m = read(),s= read();
        //scanf("%d%d%d",&n,&m,&s);
        for(int i = 0; i<m; i++)
        {
            int st,en;
            st = read(),en = read();
            //scanf("%d%d",&st,&en);
            if(st>en)//单向建图，避免重复遍历
                G[en].push_back(st);
            else
                G[st].push_back(en);
            mp[st][en] = 1,mp[en][st] = 1;//在遍历的时候用来检查是否能构成完全图
        }
        for(int i = 1; i<=n; i++)
        {
            path[1] = i;//记录拿出的可以构成完全图的点
            dfs(i,1);
            path[1] = 0;
        }
        printf("%d
",ans);
    }
    return 0;
}