Description
描述
给定一个由 $n$ 个点组成的严格凸多边形。你要将这个图形平移 $n$ 次,每次将一个顶点与原点 $(0,0)$ 重合。请判断这 $n$ 个平移后的多边形的并是否与原图形相似。
输入
第一行为一个正整数 $n$($3 le n le 10^5$)。
接下来 $n$ 行,每行两个正整数 $x_i, y_i$($|x_i|, |y_i| le 10^9$),表示一个顶点。
在读入中,保证输入的点按逆时针顺序排列,形成严格凸多边形。
输出
一行一个 YES 或 NO。
样例
输入1
4
1 0
4 1
3 4
0 3输出1
YES
输入2
3
100 86
50 0
150 0输出2
NO
输入3
8
0 0
1 0
2 1
3 3
4 6
3 6
2 5
1 3输出3
YES
解释
样例2:
剩下两个见 Solution。
Solution
致和我一样没写过计算几何的人……
前置知识:闵可夫斯基和
「闵可夫斯基和」是两个欧几里得空间的点集的和,也称为这两个空间的「膨胀集」,以德国数学家闵可夫斯基命名。点集 $A$ 与 $B$ 的闵可夫斯基和被定义为:
$$ A+B = { a+b ~|~ a in A, b in B} $$
例如,平面上有两个三角形,其坐标分别为 $A={(1,0),(0,1),(0,-1)}$ 及 $B={(0,0),(1,1),(1,1)}$ ,则其闵可夫斯基和为 $A + B = {(1, 0), (2, 1), (2,1), (0, 1), (1, 2), (1, 0), (0,1), (1, 0), (1,2)}$。通俗一点,从原点向图形 $A$ 内部的每一个点做向量,将图形 $B$ 沿每个向量移动,所有的最终位置的并便是闵可夫斯基和(具有交换律)。
现在题目已经给了我们一个点集,就叫做 $S$ 吧。
对于 $(x, y) in S$,我们要把它给平移到 $(0, 0)$ 去,就是要走一个 $(-x, -y)$,所有的在一起,便是 $-S$ 了。
然后我们发现,我们恰好是想要 从原点向图形 $-S$ 内部的每一个点做向量,将图形 $S$ 沿每个向量移动,所有的最终位置的并 这个图形,它正好就是 $S$ 与 $-S$ 的闵可夫斯基和!
然后呢,就可以爆干了。
当然这个做法不香,需要继续分析。
正常求一定是 $2n$ 条边,所以有边共线。然后我们发现,与 $S$ 相似的答案多边形,与 $S$ 的相似比恰好为 $2$!
这从样例中很容易看出来。
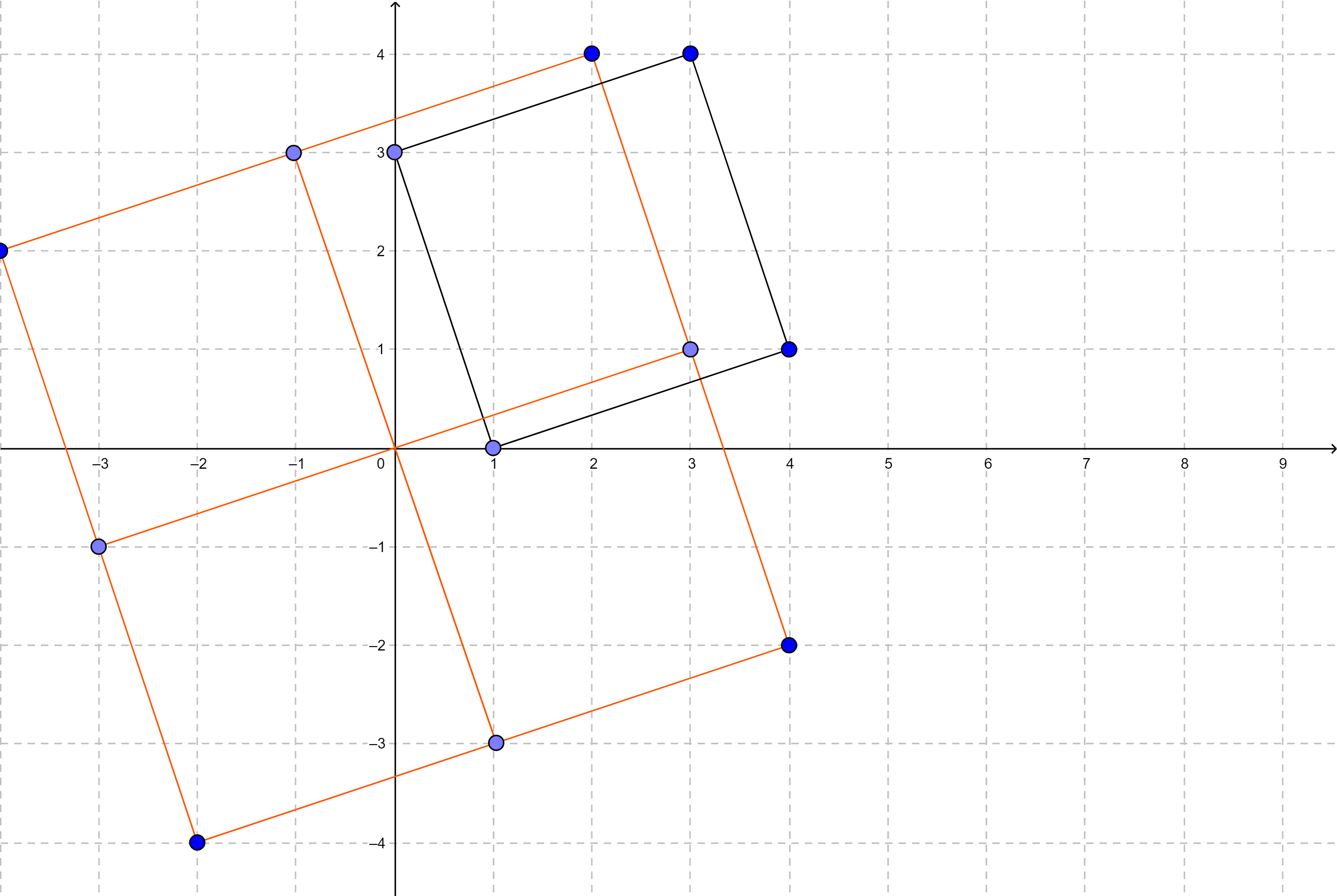
样例1:
样例3:
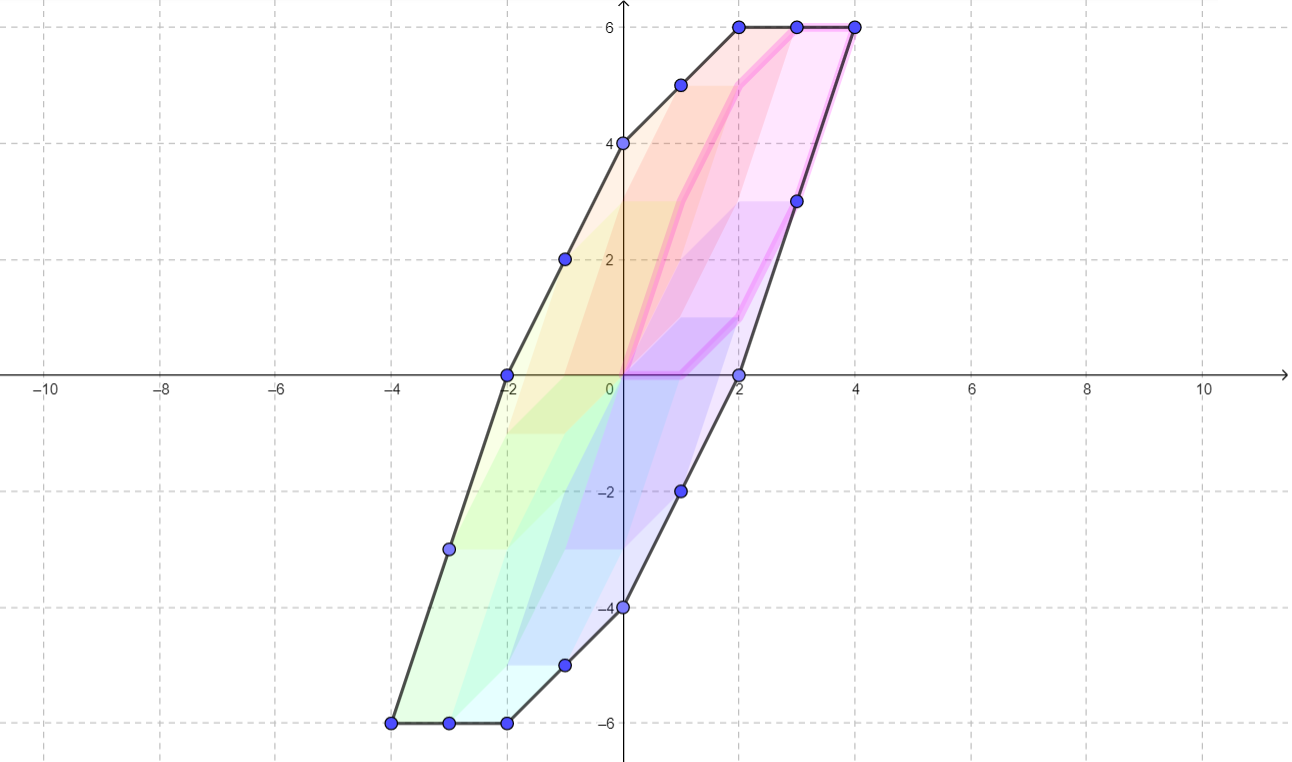
从图中很明显可以看出来,临边相等且共线,而且它来自 两个相邻多边形的同一条边,而这次的平移取决于 它对面的那条边。
- 不重合,说明对边与它相等;
- 共线,说明对边与它平行。
所以,这题就是让我们判断,这个图形是否 中心对称!
于是检查对应点连线的中点是否重合就行了。
时间复杂度 $mathcal O(n)$。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const double EPS = 1e-10;
double x[N], y[N];
int main()
{
ios::sync_with_stdio(false);
int n;
cin >> n;
for(int i = 1; i <= n; i++) cin >> x[i] >> y[i];
if(n & 1) { cout << "NO
"; return 0; }
int mid = n >> 1;
double px = (x[1] + x[mid + 1]) / 2.0;
double py = (y[1] + y[mid + 1]) / 2.0;
bool ok = true;
for(int i = 2; i <= mid; i++)
{
double kx = (x[i] + x[mid + i]) / 2.0;
double ky = (y[i] + y[mid + i]) / 2.0;
if(fabs(px - kx) >= EPS || fabs(py - ky) >= EPS) ok = false;
}
if(ok) cout << "YES
";
else cout << "NO
";
return 0;
}
