题目地址:http://acm.hdu.edu.cn/showproblem.php?pid=2063
摘录于互联网,原创作者redraiment,很详细的二分图匹配入门资料!
2063 过山车
Problem Description
RPG girls今天和大家一起去游乐场玩,终于可以坐上梦寐以求的过山车了。可是,过山车的每一排只有两个座位,而且还有条不成文的规矩,就是每个女生必须找个个男生做partner和她同坐。但是,每个女孩都有各自的想法,举个例子把,Rabbit只愿意和XHD或PQK做partner,Grass只愿意和linle或LL做partner,PrincessSnow愿意和水域浪子或伪酷儿做partner。考虑到经费问题,boss刘决定只让找到partner的人去坐过山车,其他的人,嘿嘿,就站在下面看着吧。聪明的Acmer,你可以帮忙算算最多有多少对组合可以坐上过山车吗?
Input
输入数据的第一行是三个整数K , M , N,分别表示可能的组合数目,女生的人数,男生的人数。0<K<=1000
1<=N 和M<=500.接下来的K行,每行有两个数,分别表示女生Ai愿意和男生Bj做partner。最后一个0结束输入。
Output
对于每组数据,输出一个整数,表示可以坐上过山车的最多组合数。
Sample Input
6 3 3
1 1
1 2
1 3
2 1
2 3
3 1
0
Sample Output
3
Author
PrincessSnow
问题分析
Problem Analyse
求二分图最大匹配
需要离散数学图论的知识。
Algorithm Analyse
做这一题的时候,也费了我大力气。以前都没涉及过二分图的算法,对这方面的知识可以说是零;另一面网上的资料都很零散。没有比较系统比较完整地介绍一下的。我也是在百度里搜索了很多资料,才了解并熟悉这个算法,最后能一次性通过,并且排名排在第一位,我真的是太兴奋了!为了方便后来者,也方便我自己以后查阅(与人方便,与己方便嘛),我把搜集的资料整理一下,加上一点自己的心得,把它们写下来。
二分图的基本概念
一个无向图G=<V, E>,如果存在两个集合X、Y,使得X∪Y=V, X∩Y=Φ,并且每一条边e={x,y}有x∈X,y∈Y,则称G为一个二分图(bipartite graph)。常用<X, E, Y>来表示一个二分图。若对X中任一x及Y中任一y恰有一边e∈E,使e = {x, y}, 则称G为完全二分图(complete bipartite graph)。当|X| = m,|Y| = n时,完全二分图G记为Km,n。
二分图的性质:
定理:无向图G为二分图的充分必要条件是,G至少有两个顶点,且其所有回路的长度均为偶数。
匹配:设G=<V, E>为二分图,如果M⊆E,并且M中没有任何两边有公共端点。M=Φ时称M为空匹配。
最大匹配:G的所有匹配中边数最多的匹配称为最大匹配。
完全匹配:若X(Y)中所有的顶点都是匹配M中的端点。则成M为完全匹配。若M既是X-完全匹配又是Y-完全匹配,则称M为G的完全匹配。
注意:最大匹配总是存在但未必唯一;X(Y)-完全匹配及G的完全匹配必定是最大的,但反之则不然;X(Y)-完全匹配未必存在。
下面引入几个术语:
设G=<V, E>为二分图,M为G的一个匹配。
- M中边的端点称为M-顶点,其它顶点称为非M-顶点。
- 增广路径:除了起点和终点两个顶点为非M-顶点,其他路径上所有的点都是M=顶点。而且它的边为匹配边、非匹配边交替出现。
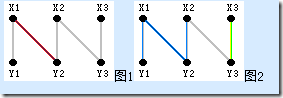
如上图中图1,就是一个二分图的匹配:[X1, Y2]。图2就是在这个匹配的基础上的两个增广路径:X2→Y2→X1→Y1和X3→Y3。
我们来验证一下:增广路径 X2→Y2→X1→Y1中,起止点X2、Y1为非M-顶点。而中间点Y2、X1都是M-顶点。
边{X2, Y2}, {X1, Y1}为非匹配边,而边{Y2, X1}为匹配边,满足匹配边与非匹配边交替出现。
同理X3→Y3路径也满足增广路径的要求。借助这幅图,来描述一下增广路径的性质。
- 有奇数条边。
- 起点在二分图的左半边,终点在右半边。
- 路径上的点一定是一个在左半边,一个在右半边,交替出现。(其实二分图的性质就决定了这一点,因为二分图同一边的点之间没有边相连,不要忘记哦。)
- 整条路径上没有重复的点。
- 起点和终点都是目前还没有配对的点,而其它所有点都是已经配好对的。
- 路径上的所有第奇数条边都不在原匹配中,所有第偶数条边都出现在原匹配中。
- 最后,也是最重要的一条,把增广路径上的所有第奇数条边加入到原匹配中去,并把增广路径中的所有第偶数条边从原匹配中删除(这个操作称为增广路径的取反),则新的匹配数就比原匹配数增加了1个。
又∵第一条是非匹配边 且 匹配边与非匹配边交替出现
∴非匹配边有K+1条,匹配边有K条。
非匹配边比匹配边多了1条。
此时,我们做取反操作(匹配边变成非匹配边,非匹配边变成匹配边),则匹配边的个数就会在原来的基础上增加1条。
求最大匹配的“匈牙利算法”就是这样做的。
无论从哪个匹配开始(整个程序的初始状态是从空匹配开始),每次操作都让匹配数增加1条,不断使它得到扩充,直到找不到增广路径。
这样就得到了最大匹配了。对增广路径,还有一种递归的定义,可能不大准确,但揭示了一种寻找增广路径的一般方法:
从集合X中的一个非M-顶点A出发,通过与A关联的边到达集合Y中的端点B, 如果B在M中没有任何边匹配,则B就是该增广路径的终点; 如果B已经与C点配对,则这条增广路径就是从A→B→C并加上“从C点出发的增广路径”。 并且这条增广路径中不能有重复的点出现。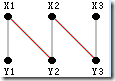
比如我们要从上图中找出一条从X3点出发的增广路径,我们需要做以下几步。- 首先从X3出发,它能连接到的点只有点Y3,而Y3已经与X2配对,所以现在的增广路径是X3→Y3→X2在加上从点X2出发的增广路径。
- 点X2能连接到Y2,Y3,但Y3与前面的路径重复,而{X2, Y2}这条边也不在原来的匹配中,所以只能连接到Y2。所以现在的增广路径是X3→Y3→X2→Y2→X1在加上从点X1出发的增广路径。
- 点X1能连接到的点且不前面路径重复的点只有Y1。并且Y1在原先的匹配中不与其他所有点配对,属于非M-顶点。因此Y1是该增广路径的终点。所以最终的增广路径是X3→Y3→X2→Y2→X1→Y1。
严格意义上讲,上面提到的从X2出发的增广路径X2→Y2→X1→Y1和从点X1出发的增广路径X1→Y1并不是真正意义上的增广路径,它们不符合第5个性质。它们的起点是已配对的点。 这里说它们是增广路径只是为了简化搜索过程,它们都只是中间返回值而已。
现在就进入我们的正题:用匈牙利算法求最大匹配。
匈牙利算法的基本模式是:
初始时最大匹配为空 while 找得到增广路径 do 把增广路径加入到最大匹配中去比如我们寻找图1的最大匹配,过程可能如下:
- 初始最大匹配为空。
- 找到增广路径X1→Y2,把它取反,则匹配数增大到1,最大匹配变成[X1, Y2]。
- 找到增广路径X2→Y3,把它取反,则匹配数增大到2,最大匹配变成[X1, Y2],[X2, Y3]。
- 找到增广路径X3→Y3→X2→Y2→X1→Y1,把它取反,则匹配数增大到3,最大匹配变成[X1, Y1],[X2, Y2],[X3, Y3]。
- 找不出增广路径,程序结束,得到最大匹配数为3。
从上面的描述可以看出,搜索增广路径的方法是DFS,写一个递归的函数。当然也可以用BFS。
至此,理论基础部份讲完了。但是要完成匈牙利算法,还需要一个重要的定理:
如果从一个点A出发,没有找到增广路径,那么无论再从别的点出发找到多少增广路径来改变现在的匹配,从A出发都永远找不到增广路径。
有了这个定理,匈牙利算法就成形了。如下:
初始时最大匹配为空 for 二分图左半边的每个点i do 从点i出发寻找增广路径。如果找到,则把它取反(即增加了总了匹配数)。
如果二分图的左半边一共有n个点,那么最多找n条增广路径。如果图中共有m条边,那么每找一条增广路径(DFS或BFS)时最多把所有边遍历一遍,所花时间也就是m。所以总的时间大概就是O(n * m)。
编码建议
Programing
知道了前面的算法,编码倒是挺快的。
数据结构:
保存二分图用的是邻接表。
为方便存储和阅读,数组下标从1开始(0那个空间就空着不用)。
因此,第i个表头邻接的是第i个女生愿意与他做partner的男生号。
集合X、Y用一维数组表示。下标同样从1开始。
如果它们暂时没有点配对,则里面保存的是O,否则保存配对的点的下标。
初始状态X、Y都为0。
因为X是从1到n循环,所以只需要判断Y集合中的点是否被访问过。
判断是否被访问过用一个Bool型一维数组,true表示被访问过,false表示未被访问过。
中间记录增广路径用栈结构。因为增广路径的边数是奇数,根据握手定理,它的顶点数一定是偶数。
找到增广路径以后,每次从栈顶取出2个端点,就是现在相互配对的端点了。一直到栈取空为止。
算法实现:
实现匈牙利算法分为4个步骤:
- 初始化:
集合X、Y清空
图清空 - 输入:
输入集合X、Y的大小size_x和size_y,以及所有的边 - 计算:
i从1循环到size_x,深搜寻找Xi的增广路径
每次寻找前要先清空栈,并且初始Visit数组为false
在深搜的过程中,要注意,如果寻找增广路径失败,要记得把刚加入的那一个顶点从栈中删除
如果增广路径查找成功,就开始读栈,对X、Y里相互配对的端点进行标记,直到栈为空 - 输出:
统计X(Y)集合中有配对的端点个数,即最大匹配数。
输出最大匹配数
编码建议
#include <stack>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef struct node
{
int ord;
node * next;
}Node;
const int size = 512 + 1;
Node list[size];
int X[size];
int Y[size];
bool visit[size];
int size_x;
int size_y;
stack <int> stk;
void init()
{
int i;
for (i = 1; i <= size_x; i++)
list[i].next = NULL;
memset(X, 0, (size_x + 1) * sizeof(int));
memset(Y, 0, (size_y + 1) * sizeof(int));
}
void input(int len)
{
int i;
int x;
int y;
Node* p;
for (i = 0; i < len; i++)
{
scanf("%d%d", &x, &y);
p = new Node;
p->ord = y;
p->next = list[x].next;
list[x].next = p;
}
}
bool dfs(int x)
{
Node* p;
stk.push(x);
for (p = list[x].next; p; p = p->next)
{
if (!visit[p->ord])
{
visit[p->ord] = true;
stk.push(p->ord);
if (!Y[p->ord] || dfs(Y[p->ord]))
return true;
else
stk.pop();
}
}
stk.pop();
return false;
}
void solve()
{
int i;
int top;
for (i = 1; i <= size_x; i++)
{
while (!stk.empty()) stk.pop();
memset(visit, false, size_y + 1);
if (dfs(i))
{
while (!stk.empty())
{
top = stk.top();
stk.pop();
Y[top] = stk.top();
X[stk.top()] = top;
stk.pop();
}
}
}
}
void output()
{
int i;
int count = 0;
Node* p;
for (i = 1; i <= size_x; i++)
{
if (X[i]) count++;
while (p = list[i].next)
{
list[i].next = p->next;
delete p;
}
}
cout << count << endl;
}
int main(void)
{
int n;
while (scanf("%d", &n), n)
{
scanf("%d%d", &size_x, &size_y);
init();
input(n);
solve();
output();
while (!stk.empty()) stk.pop();
}
return 0;
}