1. 非线性判别函数
本章介绍广义线判别函数与核函数,并分析他们的不同。
2. 广义线性判别函数
对于非线性问题,我们依旧可以使用线性分类器进行求解。
-
广义线性判别函数增加了特征的高次项,将低维特征转化为高维特征。将低维线性不可分问题转化为高维的线性可分问题,并学习到高维空间下的线性分类器,该分类器其实等价于低维的非线性分类器。
-
以经典的异或问题为例(线性不可分):
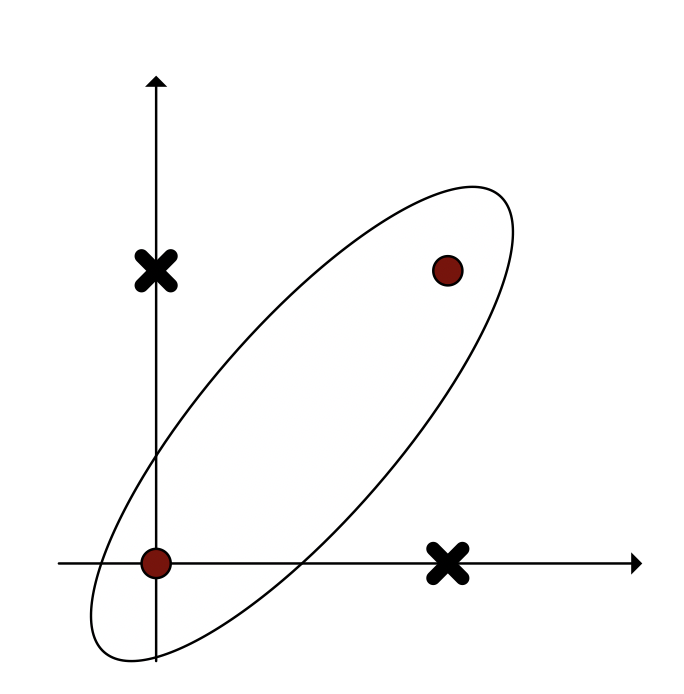
-
对于该问题的二维输入特征,引入高维特征(x_1 * x_2),即对于二维坐标(0,1),转化为三维坐标(0,1,0)。

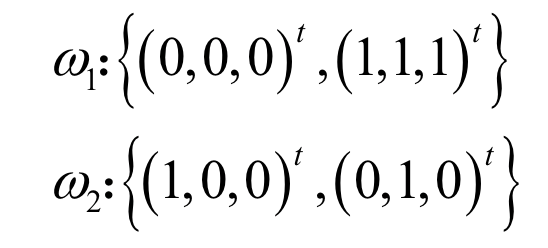
-
在扩增的的三维高维空间中学习线性判别函数:
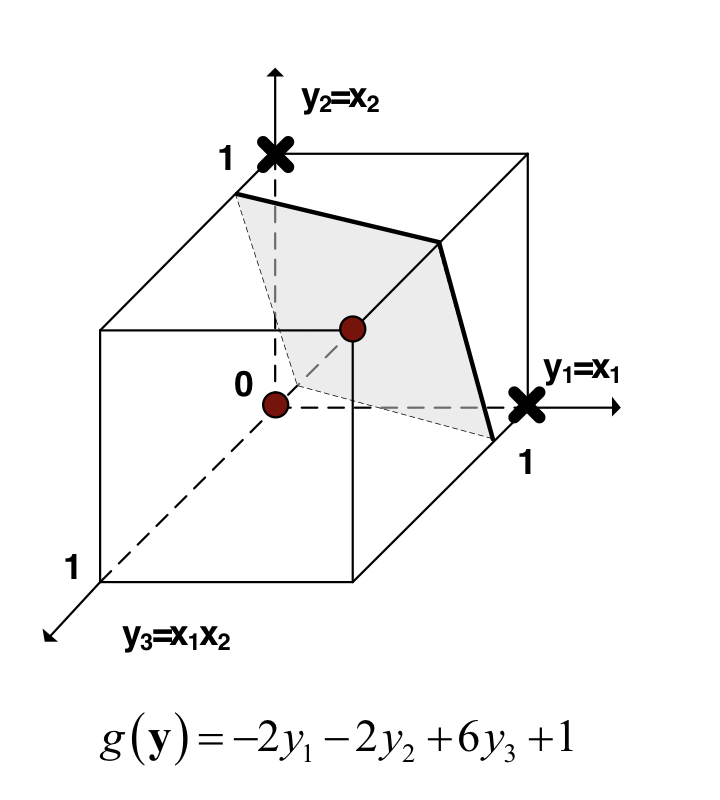
-
该线性函数等价于低维空间的非线性函数:
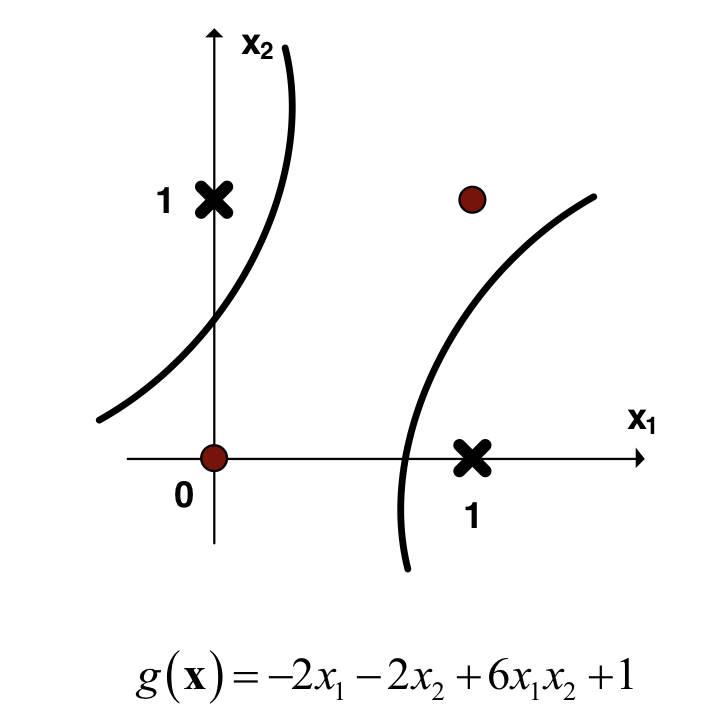
-
-
这么做的弊端是,当引入的高维特征后,会降低模型的泛化能力,易过拟合。
-
广义线性判别函数的问题:
- 阶数问题:对于一个具体问题,很难确定判别函数的阶数。
- 维数问题:当原始特征维数较大时,会造成“维数灾难”。
3. 核函数
核函数虽然也是将特征从低维空间映射到高维空间,但是可以很好的避免广义线性判别函数的维数灾难问题。
接下来介绍核函数的主要思想,之后举例介绍核函数是怎么避免维数灾难的。
3.1 核函数基本思想
- 启示:特征空间中两个矢量之间的内积可以通过定义输入空间中的核函数直接计算得到。
- 实现方法:不必定义非线性映射,而直接在输入空间中定义核函数(K)来完成非线性映射。
- 应用条件:
- 定义的核函数(K)能够对应于特征空间中的内积;
- 识别方法中不需要计算特征空间中的矢量本身,而只须计算特征空间中两个矢量的内积。
3.2 核函数举例说明
- 对于下列输入空间的非线性问题,通过非线性映射,转化为高维空间的线性可分问题:
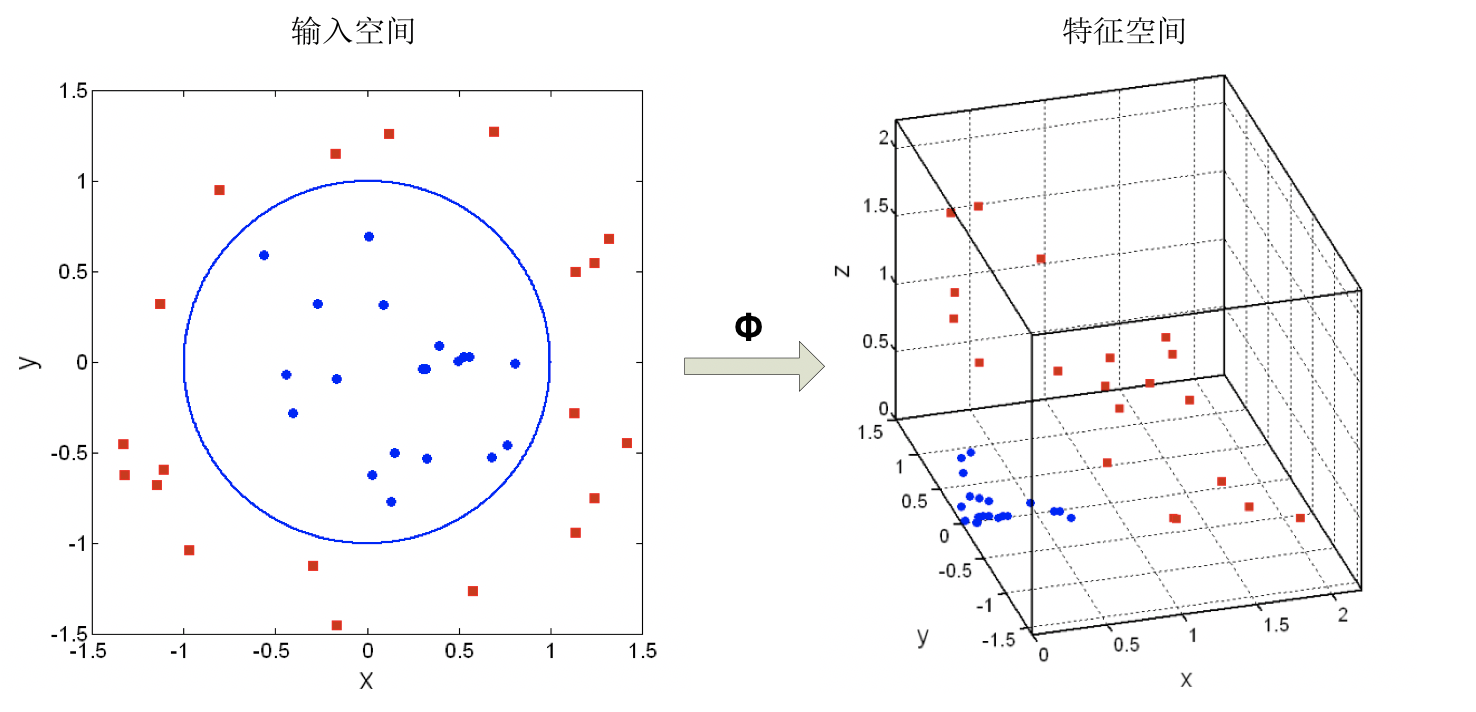
- 非线性映射函数为:
[Phi : left( x _ { 1 } , x _ { 2 }
ight) ^ { t }
ightarrow left( x _ { 1 } ^ { 2 } , sqrt { 2 } x _ { 1 } x _ { 2 } , x _ { 2 } ^ { 2 }
ight) ^ { t }
]
- 计算特征空间中两个矢量的内积:
[egin{aligned} Phi ( mathbf { x } ) ^ { t } Phi ( mathbf { y } ) & = left( x _ { 1 } ^ { 2 } , sqrt { 2 } x _ { 1 } x _ { 2 } , x _ { 2 } ^ { 2 }
ight) left( y _ { 1 } ^ { 2 } , sqrt { 2 } y _ { 1 } y _ { 2 } , y _ { 2 } ^ { 2 }
ight) ^ { t } \ & = x _ { 1 } ^ { 2 } y _ { 1 } ^ { 2 } + 2 x _ { 1 } x _ { 2 } y _ { 1 } y _ { 2 } + x _ { 2 } ^ { 2 } y _ { 2 } ^ { 2 } \ & = left( x _ { 1 } y _ { 1 } + x _ { 2 } y _ { 2 }
ight) ^ { 2 } \ & = left( mathbf { x } ^ { t } mathbf { y }
ight) ^ { 2 } end{aligned}
]
- 定义核函数(K ( mathbf { x } , mathbf { y } ) = left( mathbf { x } ^ { t } mathbf { y } ight) ^ { 2 }),则有:
[Phi ( mathbf { x } ) ^ { t } Phi ( mathbf { y } ) = K ( mathbf { x } , mathbf { y } )
]
- 在这个例子中,特征空间中的内积,可以用输入空间的核函数计算得到,从而不需要计算高维空间的矢量具体是什么,也就避免的维数灾难问题。
3.3 常用的核函数
- 高斯 Gaussian RBF:(K ( mathbf { x } , mathbf { y } ) = exp left( - frac { | mathbf { x } - mathbf { y } | ^ { 2 } } { sigma } ight))
- 多项式 Polynomial:(K ( mathbf { x } , mathbf { y } ) = left( left( mathbf { x } ^ { t } mathbf { y } ight) + 1 ight) ^ { d })