一道数据结构模板,但分两种情况,难度相同,时间复杂度都是 O(n log n)的。
先介绍下树状数组支持的操作:
1. 区间和、区间异或和、区间乘积和RMQ(显然,支持的操作都具有交换律,这也算是树状数组的一大特性吧);
2. 单点修改(朴素的树状数组结构不支持区间修改,当然也可以普及成区间修改结构)。
提前预备一种位运算操作 lowbit(取一个二进制数 x 的最后一位“ 1”): x and (-x);
树状数组的原理图是这样的:
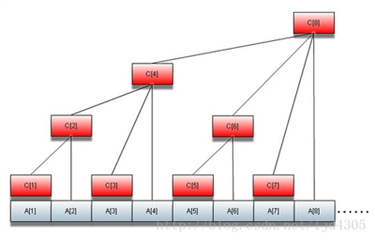
其实就是数组中某个位置存储一段区间(长度为 2k,k 为正整数)的值。
至于 k 的玄学算法(也不算玄学吧),可以去洛谷看题解(此图也是 CO 过来的)。
程序中的 change 函数是用来修改一些会覆盖到 x 的区间所对应的数组中的位置的值(x+x and (-x) 是找下一个覆盖到 x 的区间所对应的数组中的位置)。
如:当 a[5]+y 时,x=5: 1. c[x]:=c[x]+y; 即 c[5]:=c[5]+y;(此时x=5,然后找下一位 x=x+x and (-x) 就是 00101+00001=00110=6,x 变成6)
2. c[x]:=c[x]+y; 即 c[6]:=c[6]+y;(此时x=6,然后找下一位 x=x+x and (-x) 就是 00110+00010=01000=8,x 变成8)
(看图,修改 c[6],因为 c[6] 覆盖了 a[5])
3. c[x]:=c[x]+y; 即 c[8]:=c[8]+y;(此时x=8,然后找下一位 x=x+x and (-x) 就是 01000+01000=10000=16,x 变成16)
(看图,修改 c[8],因为 c[8] 覆盖了 a[5])
............(当 x>n 时就不用继续做了,无用)
程序中的 que 函数是用来求区间 1~x(x 为数组的某一位置)的值(x-x and (-x) 是将当前数组中 x 位置所覆盖的区域减掉,剩下的就是区间 1~x 中 x 位置没有覆盖到的长度,即没有覆盖到的最后一个位置)。
由于没有覆盖的区间是连续的,所以可以从没有覆盖到的最后一个位置继续求值。
如:当求 1~7 的区间和时,x=7: 1. que:=que+c[x]; 即 que:=que+c[7];(此时x=7,x=x-x and (-x) 就是 0111-0001=0110=6,x 变成6)
(看图,数组 c[7] 未覆盖到区间 1~6)
2. que:=que+c[x]; 即 que:=que+c[6];(此时x=6,x=x-x and (-x) 就是 0110-0010=0100=4,x 变成4)
(看图,数组 c[6] 未覆盖到区间1~4)
3. que:=que+c[x]; 即 que:=que+c[4];(此时x=4,x=x-x and (-x) 就是 0100-0100=0000=0,x 变成0)
(当 x=0 时,所有区间都统计完,退出)
First:修改单个数(此题是加上某个数),求操作后的区间值(这里指区间中所有数的和)。
题目:洛谷 P3374

1 var 2 a:array[0..1000001] of longint; 3 i,j,k,m,n,x:longint; 4 procedure change(x,y:longint); 5 begin 6 while x<=n do 7 begin 8 a[x]:=a[x]+y; 9 x:=x+x and (-x); 10 end; 11 end; 12 function que(x:longint):longint; 13 begin 14 que:=0; 15 while x>0 do 16 begin 17 que:=que+a[x]; 18 x:=x-x and (-x); 19 end; 20 end; 21 begin 22 readln(n,m); 23 for i:=1 to n do 24 begin 25 read(j); 26 change(i,j); 27 end; 28 readln; 29 for i:=1 to m do 30 begin 31 readln(j,k,x); 32 if j=1 then change(k,x) else writeln(que(x)-que(k-1)); 33 end; 34 end.
Second:修改区间值(此题是区间内每个数加上某个数),求操作后单个数的值。
题目:洛谷 P3368

1 var 2 a,b:array[0..1000001] of longint; 3 i,j,k,m,n,x:longint; 4 procedure change(x,y:longint); 5 begin 6 while x<=n do 7 begin 8 b[x]:=b[x]+y; 9 x:=x+x and (-x); 10 end; 11 end; 12 function que(x:longint):longint; 13 begin 14 que:=0; 15 while x>0 do 16 begin 17 que:=que+b[x]; 18 x:=x-x and (-x); 19 end; 20 end; 21 begin 22 readln(n,m); 23 for i:=1 to n do 24 read(a[i]); 25 readln; 26 for i:=1 to m do 27 begin 28 read(k,j); 29 if k=1 then begin 30 readln(k,x); 31 change(j,x); 32 change(k+1,-x); 33 end else writeln(a[j]+que(j)); 34 end; 35 end.
其实说白了就是灵活利用位运算使数组变成树形结构来存储区间内容,从而完成区间操作与查询。
树状数组功能与线段树类似,思想也类似,只是全部简单化了而已,各有优缺点,就不一一列举了,自行做题体会。
然后解释什么的自己上洛谷点题解看,没什么好说的哎,能理解线段树就能理解这个。
