写下来的原因,是觉得这个对我来说有纪念意义(大佬勿喷,虽然没有大佬会看……)。第一次主动写总结,真的是好激动呢。

先做了这一题,然后在下一题里面给了自己点启发。
题目是这样子的:
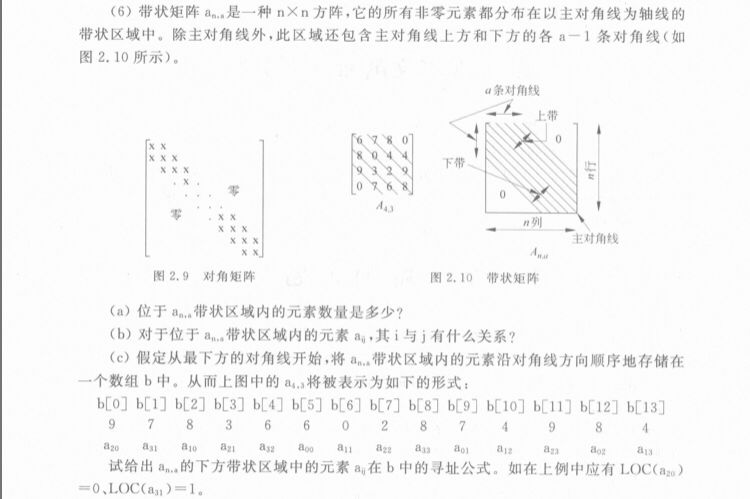
ps:这题我也不知道标准答案,自己的拙劣方法,感觉还有有更好的更简便的方法。
用到的数学知识:

已知等差数列 首项为a,公差为d,共有n项。Sn = n * a + n * (n-1) * d / 2 (我也没背,只记得首项加尾项乘以项数除以2的口诀,再推导)
推导式子:a + a+d + a+2d + …… + a + (n - 1)d = (2a + (n - 1)d ) * n / 2 (***)= n * a + n * (n-1) * d / 2
(a) 主对角线上下方各a-1条对角线
容易发现:主对角线上有n个元素,相邻的每隔一条会减少一个元素。
##1 不算主对角线的n个元素,剩下的 a-1 条对角线元素依次为: n - 1,n - 2 ,……,n - (a - 1) 再等差数列求和 再乘以2 再加上n即为答案
用上面的 式子就可不用一 一列出尾项,公差为-1,首项为n - 1 ,项数为a - 1条, 带入可直接得到这部分个数和。
不过我更喜欢 (***)式子的表示形式:为(2n - a) * ( a - 1) / 2
所以答案为 : (2n - a) * (a - 1) + n
(b) 这题靠感觉吧,观察矩阵的下标,再尝试性将a赋予不同的值观察。

发现,| i - j | = a - 1 时 为带状区域的边界
| i - j | 的值越大,那么对应位置的元素越靠近左下角和右上角。
所以本题答案为:| i - j | <= a - 1
(c) 这小题让我很想记录下这个题目。以及我的思维过程
以前听课,老师讲过行序列序,没讲过按对角线序存储。
这题本质就是找到aij 这个元素在一维矩阵中是第几个元素。
根据(b)题的启发,我们可以发现,根据i - j 的值可以轻松的发现aij 这个元素在第几条对角线上。
当i - j = a - 1 时就是第一条对角线, 为 a - 2 时为第二条对角线, 为0 时 主对角线, 2 - a 时 倒数第二条对角线, 1 - a 时为倒数第一条对角线。
发现了在第几条对角线,之后看到两侧的第一条对角线和倒数第一条对角线元素个数为n - (a - 1)个(可以根据文中 ##1 标记处发现)就又是等差数列的问题。
这里还需要分类讨论,因为在二维数组中主对角线两侧的元素位置对称的情况下,在一维数组中位置并不对称。
分i >= j 和 i <= j讨论。
i >= j 时:
发现 a - 1 - (i - j)就意味着,在aij 所在的对角线前,一共有几条对角线,也就是等差数列的项数,第一条对角线的数目为 n - (a - 1),即为首项,元素个数以1递增
又发现,在i >= j条件下aij,的 j值 就表示其在那条对角线上,元素位置为 第 j + 1 个。
也就是说,aij 是前面所有对角线元素个数和,加上j+1,在对应一维数组中的寻址位置也就是再减一。
具体计算小心一点就可得出答案。
i < j 时:
在下面a-1条及主对角线的基础上,在上半区域里面,即上面的a-1条对角线里面再开始大体相同的计算。
发现 0 - (i - j)- 1就意味着,在aij 所在的对角线前,一共有几条对角线,即项数,首项是 n - 1,元素个数以1递减。
对应发现,aij 的 i值 就表示在那条对角线上,元素位置为第 i + 1 个
再加上前面的a条对角线一共的总数目,得到这个是第几个位置的元素,再减一,即为对应一维数组中的寻址地址。
答案(经过验算的..)为:
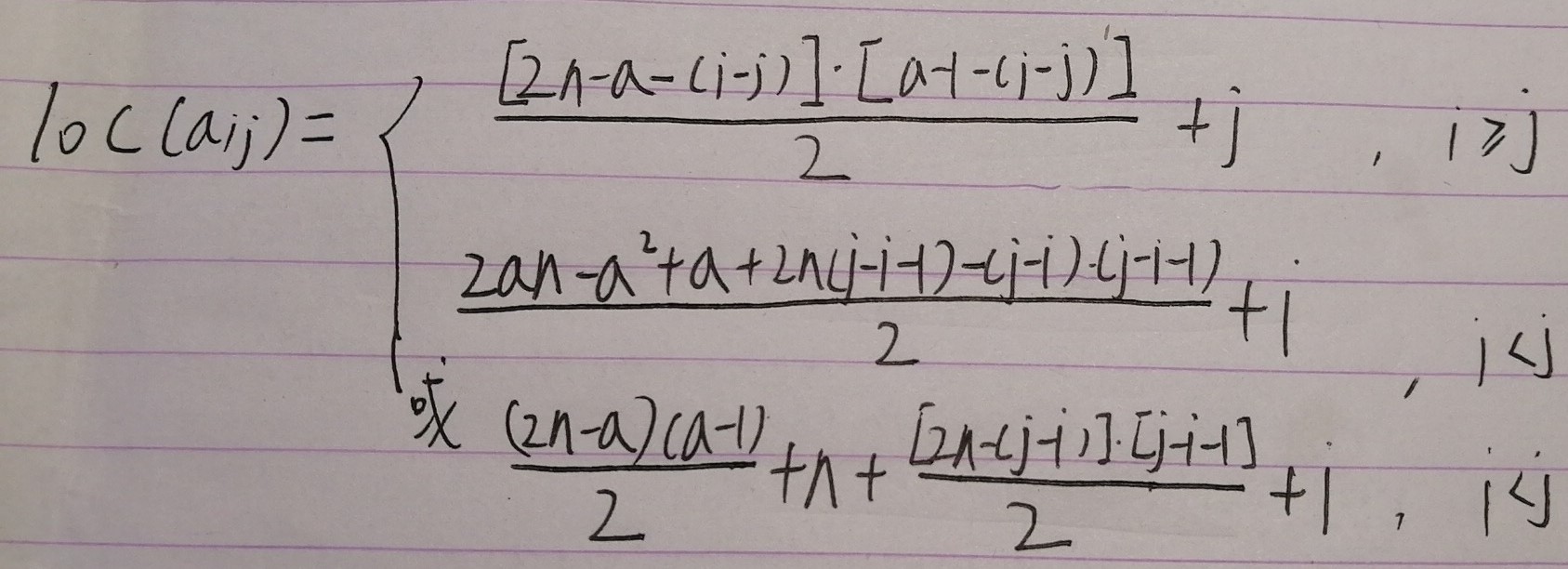
ps:本想将第二个式子拆开找与i >= j情况下式子的微妙关系,尝试合并,结果是徒劳,然后还是觉得原来不拆开的式子好看。
