洛谷P1901 发射站
题目描述
某地有 N 个能量发射站排成一行,每个发射站 i 都有不相同的高度 Hi,并能向两边(当 然两端的只能向一边)同时发射能量值为 Vi 的能量,并且发出的能量只被两边最近的且比 它高的发射站接收。
显然,每个发射站发来的能量有可能被 0 或 1 或 2 个其他发射站所接受,特别是为了安 全,每个发射站接收到的能量总和是我们很关心的问题。由于数据很多,现只需要你帮忙计 算出接收最多能量的发射站接收的能量是多少。
输入输出格式
输入格式:
第 1 行:一个整数 N;
第 2 到 N+1 行:第 i+1 行有两个整数 Hi 和 Vi,表示第 i 个人发射站的高度和发射的能量值。
输出格式:
输出仅一行,表示接收最多能量的发射站接收到的能量值,答案不超过 longint。
这题跟洛谷P2947比较像,那个是只能向右边发射,这个加上左边就好了。
那么我们考虑只能向右边发射的情况,从右向左维护队首最大一个单调队列,如果队首就是当前元素,那么它没有可以辐射到的,因为他自己就是当前队列里最大的。
否则,因为当前元素在队尾,它之前那个元素一定是即离它最近又比他高,所以可以被他辐射到。
左边同理。。。

#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; struct node{ int x,dfn; }team[1000001]; struct sz{ int h,v; }a[1000001]; long long n,m,tail,head; long long i,j,b[1000001]; long long ans[1000001],maxn; inline int read(){ int x=0,f=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-') f=-1; ch=getchar();} while(ch<='9' && ch>='0'){x=x*10+ch-'0'; ch=getchar();} return x*f; } void write(long long x){ if(x<10){putchar(x%10+48); return;} write(x/10); putchar(x%10+48); } int main(){ n=read(); for (i=1; i<=n; i++) a[i].h=read(),a[i].v=read(); head=1; tail=1; team[head].x=a[n].h; team[head].dfn=n; b[n]=0; for (i=n-1; i>=1; i--){ while (head<=tail&&a[i].h>=team[tail].x) tail--; tail++; team[tail].x=a[i].h; team[tail].dfn=i; if (team[head].x<=a[i].h) b[i]=0; else{ b[i]=team[tail-1].dfn; ans[b[i]]+=a[i].v; } } head=1; tail=1; team[head].x=a[1].h; team[head].dfn=1; b[n]=0; for (i=2; i<=n; i++){ while (head<=tail&&a[i].h>=team[tail].x) tail--; tail++; team[tail].x=a[i].h; team[tail].dfn=i; if (team[head].x<=a[i].h) b[i]=0; else{ b[i]=team[tail-1].dfn; ans[b[i]]+=a[i].v; } } for (i=1; i<=n; i++) if (ans[i]>maxn) maxn=ans[i]; write(maxn); return 0; }
洛谷 P1823 [COI2007] Patrik 音乐会的等待
题目描述
N个人正在排队进入一个音乐会。人们等得很无聊,于是他们开始转来转去,想在队伍里寻找自己的熟人。队列中任意两个人A和B,如果他们是相邻或他们之间没有人比A或B高,那么他们是可以互相看得见的。
写一个程序计算出有多少对人可以互相看见。
输入输出格式
输入格式:
输入的第一行包含一个整数N (1 ≤ N ≤ 500 000), 表示队伍中共有N个人。
接下来的N行中,每行包含一个整数,表示人的高度,以毫微米(等于10的-9次方米)为单位,每个人的调度都小于2^31毫微米。这些高度分别表示队伍中人的身高。
输出格式:
输出仅有一行,包含一个数S,表示队伍中共有S对人可以互相看见。
这题其实单调队列并不难,但2018.6.29后加了三组数据,把我第一遍打的方法卡掉了,于是又写了一个记忆化过去了。
一开始循环里是这样的
for (i=n-1; i>=1; i--){ int x=tail; while (team[x]<=a[i]&&x>=head) x--; ans+=tail-x; if (team[x]>a[i]) ans++; while (head<=tail&&team[tail]<a[i]) tail--; tail++; team[tail]=a[i]; }
之后就会发现第一个while那里会被恶意数据卡掉,我们考虑优化。
设v[i]是i后面与i一样高的人的个数,初值是1。
这样我们在处理i时,可以把统计和弹出队尾元素放到一个while里,并且将相等的元素也弹出,若a[j]==a[i],v[i]+=v[j];
代码:
#include<cstdio> #include<iostream> using namespace std; struct node{ int h,v; }team[500001]; int i,n,head,tail; int j,a[500001]; long long ans; inline int read(){ int x=0,f=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-') f=-1; ch=getchar();} while(ch<='9' && ch>='0'){x=x*10+ch-'0'; ch=getchar();} return x*f; } int main(){ n=read(); for (i=1; i<=n; i++) a[i]=read(); head=1; tail=1; team[head].h=a[n]; team[head].v=1; for (i=n-1; i>=1; i--){ long long y=1; while (head<=tail&&team[tail].h<=a[i]){ ans+=team[tail].v; if (team[tail].h==a[i]) y+=team[tail].v; tail--; } if (team[tail].h>a[i]) ans++; tail++; team[tail].h=a[i]; team[tail].v=y; } printf("%lld",ans); return 0; }
洛谷 P2216 [HAOI2007]理想的正方形
题目描述
有一个a*b的整数组成的矩阵,现请你从中找出一个n*n的正方形区域,使得该区域所有数中的最大值和最小值的差最小。
输入输出格式
输入格式:
第一行为3个整数,分别表示a,b,n的值
第二行至第a+1行每行为b个非负整数,表示矩阵中相应位置上的数。每行相邻两数之间用一空格分隔。
输出格式:
仅一个整数,为a*b矩阵中所有“n*n正方形区域中的最大整数和最小整数的差值”的最小值。
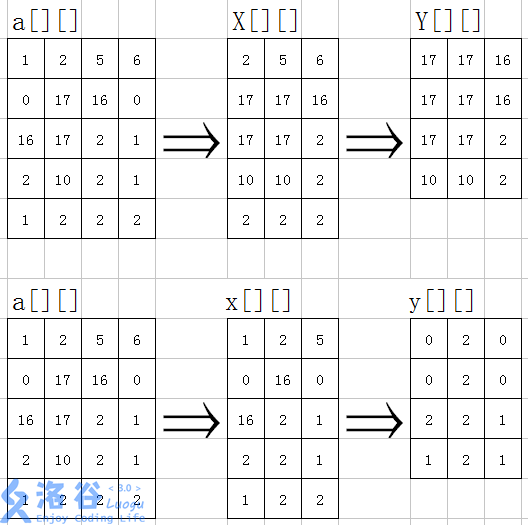
二维单调队列,图片来自于洛谷 病名為愛 的题解。
题目要求是求出一个极差最小的n*n的子矩阵,我们仔细研究一下a*b*n2的暴力就会发现,这个暴力之所以不对,是因为它重复做了很多事情,例如,我们在计算以(1,2)为左上角的正方形时,判断了很多(1,1)为左上角的正方形的元素。
正解:直接求极值不好求,我们可以先求最大值(图中的大写X,Y),X[i][j]表示第i行第j个元素后面n个元素的最大值,这个我们可以用单调队列a*b的做出来。
自己模拟一下就可以发现,x[i][j]就是以(i,j)为左上角的正方形的第一行的极值,那么这个正方形的最大值一定在X[i][j],X[i+1][j]..X[i+n-1][j]之间。
Y数组储存的就是这个值,我们可以以列号(j)为外层循环,把上面的求X的操作改一下。
同理,最小值也可以用这种方法求出来,之后可以直接求极差。
#include<cstdio> #include<iostream> using namespace std; int n,i,team1[1001],tail1,head1; int m,j,team2[1001],tail2,head2; int b1[1001][1001],c1[1001][1001]; int b2[1001][1001],c2[1001][1001]; int k,a[1001][1001],ans=1e9; inline int read(){ int x=0,f=1;char ch=getchar(); while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} while (ch<='9'&&ch>='0'){x=x*10+ch-'0';ch=getchar();} return x*f; } int main(){ n=read(); m=read(); k=read(); for (i=1; i<=n; i++) for(j=1; j<=m; j++) a[i][j]=read(); for (i=1; i<=n; i++){ head1=head2=1; tail1=tail2=0; for (j=1; j<=k-1; j++){ while (head1<=tail1&&a[i][team1[tail1]]<=a[i][j]) tail1--; while (head2<=tail2&&a[i][team2[tail2]]>=a[i][j]) tail2--; tail1++; tail2++; team1[tail1]=team2[tail2]=j; } for (j=k; j<=m; j++){ while (head1<=tail1&&a[i][team1[tail1]]<=a[i][j]) tail1--; while (head2<=tail2&&a[i][team2[tail2]]>=a[i][j]) tail2--; tail1++; team1[tail1]=j; tail2++; team2[tail2]=j; while (head1<=tail1&&j-team1[head1]>=k) head1++; while (head2<=tail2&&j-team2[head2]>=k) head2++; b1[i][j-k+1]=a[i][team1[head1]]; b2[i][j-k+1]=a[i][team2[head2]]; } } for (i=1; i<=m-k+1; i++){ head1=head2=1; tail1=tail2=0; for (j=1; j<=k-1; j++){ while (head1<=tail1&&b1[team1[tail1]][i]<=b1[j][i]) tail1--; while (head2<=tail2&&b2[team2[tail2]][i]>=b2[j][i]) tail2--; tail1++; tail2++; team1[tail1]=team2[tail2]=j; } for (j=k; j<=n; j++){ while (head1<=tail1&&b1[team1[tail1]][i]<=b1[j][i]) tail1--; while (head2<=tail2&&b2[team2[tail2]][i]>=b2[j][i]) tail2--; tail1++; team1[tail1]=j; tail2++; team2[tail2]=j; while (head1<=tail1&&j-team1[head1]>=k) head1++; while (head2<=tail2&&j-team2[head2]>=k) head2++; c1[j-k+1][i]=b1[team1[head1]][i]; c2[j-k+1][i]=b2[team2[head2]][i]; // ans=min(c1[j-k+1][i]-c2[j-k+1][i],ans); } } for (i=1; i<=n-k+1; i++) for (j=1; j<=m-k+1; j++) ans=min(ans,c1[i][j]-c2[i][j]); if (ans==0) ans=n; printf("%d ",ans); // for (i=1; i<=n-k+1; i++){ 用于调试输出 // for (j=1; j<=m-k+1; j++) // printf("%d ",c1[i][j]); // printf(" "); // } return 0; }
洛谷 P2422 良好的感觉
题目描述
kkk做了一个人体感觉分析器。每一天,人都有一个感受值Ai,Ai越大,表示人感觉越舒适。在一段时间[i, j]内,人的舒适程度定义为[i, j]中最不舒服的那一天的感受值 * [i, j]中每一天感受值的和。现在给出kkk在连续N天中的感受值,请问,在哪一段时间,kkk感觉最舒适?
输入输出格式
输入格式:
第一行为N,代表数据记录的天数
第二行N个整数,代表每一天的感受值
输出格式:
一行,表示在最舒适的一段时间中的感受值。
这题看的时候想了好久都没有想出来,最后看的xMinh学长的题解,这里提供附上来自学长的思路。
这个题的单调队列很明显是一个没有时间限制的,所以只需要考虑队中元素是什么的问题。我们可以注意到,这个题的数据范围规定没有负数,所以前缀和绝对是会越来越大的,所以队中元素应该是那个最不舒服的值。
然后转念想一想,如果这题是一个数据小的普通DP怎么做?那就是找到每个点左边那个比它小的,以及右边那个比它小的。这左右边界之间的,就是这个点最多能管到的范围。对于单调队列来说,我们可以维护一个单调递增的队列,然后往外踢的时候,被踢掉的点就找到了“右边那个比它小的”,维护完队列之后,队列中位于当前元素前一个的那个元素就是“左边那个比它小的”。这样就可以计算某个点能管到的范围了,最后再乘以这个点本身的值,比较出最大值就好了。
当然还有一个问题,如果某个点一直没有被踢掉怎么办?好办,在序列的最后加一个值为0的元素,就可以在最后一次循环踢掉所有队中元素,完成最后的处理。
PS:其实这题的数据结构严格来说叫做单调栈。
贴一下我自己的代码

#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; long long team[100001],head,tail,i,f[100001]; long long n,a[100001],s[100001],ans; inline char gc(){ static char now[1<<16],*S,*T; if(T==S){T=(S=now)+fread(now,1,1<<16,stdin);if (T==S) return EOF;} return *S++; } inline int read(){ int x=0,f=1;char ch=gc(); while(ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=gc();} while(ch<='9'&&ch>='0') x=x*10+ch-'0',ch=gc(); return x*f; } int main(){ n=read(); // scanf("%d",&n); for (i=1; i<=n; i++){ a[i]=read(); // scanf("%d",&a[i]); s[i]=s[i-1]+a[i]; } a[n+1]=0; head=1; tail=0; for (i=1; i<=n+1; i++){ while (head<=tail&&a[team[tail]]>a[i]){ f[team[tail]]+=(s[i-1]-s[team[tail]]); tail--; } f[i]=s[i]-s[team[tail]]; tail++; team[tail]=i; } for (i=1; i<=n; i++) ans=max(ans,f[i]*a[i]); printf("%lld",ans); return 0; }
luogu P3572 [POI2014]PTA-Little Bird
题意(还是来自xMinh学长的blog):
有一排n棵树,第i棵树的高度是Di。
有一些ZSH要从第一棵树到第n棵树去找他的妹子玩。
如果ZSH在第i棵树,那么他可以跳到第i+1,i+2,…,i+k棵树。
如果ZSH跳到一棵不矮于当前树的树,那么他的劳累值会+1,否则不会。
为了有体力和妹子玩,ZSH要最小化劳累值。
输入描述:
第一行输入有n棵树;
第二行输入这n棵数的高度;
第三行输入有p个ZSH;
第4~p+3行输入这个ZSH可以跳多远;
输出描述:
共p行,每一行输出一个ZSH的劳累值。
原文: https://xminh.github.io/2018/01/20/%E5%8D%95%E8%B0%83%E9%98%9F%E5%88%97-%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0.html
很普通的单调队列优化DP,首先简单的DP就是如果要跳到i,那么一定是从i之前k个点中取一个最大的,再看看是否要劳累值+1就好了,然后用单调队列把f放入队列里,维护一个递增的单调队列。
注意:去除重复元素的时候记得当f值一定时,如果队尾那个元素比i高,要把它留下。
没了。。。

#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; long long team[1000001],t,a[1000001]; long long n,i,head,tail,k,f[1000001]; inline char gc(){ static char now[1<<16],*S,*T; if(T==S){T=(S=now)+fread(now,1,1<<16,stdin);if (T==S) return EOF;} return *S++; } inline int read(){ int x=0,f=1;char ch=gc(); while(ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=gc();} while(ch<='9'&&ch>='0') x=x*10+ch-'0',ch=gc(); return x*f; } void write(int x){ if(x<10){putchar(x%10+48); return;} write(x/10); putchar(x%10+48); } int main(){ n=read(); // scanf("%lld",&n); for (i=1; i<=n; i++) a[i]=read(); // scanf("%lld",&a[i]); // scanf("%lld",&t); t=read(); while (t--){ // scanf("%lld",&k); k=read(); head=1; tail=1; memset(f,0,sizeof(f)); team[tail]=1; for (i=2; i<=n; i++){ while (head<=tail&&i-team[head]>k) head++; f[i]=f[team[head]]; if (a[i]>=a[team[head]]) f[i]++; while (head<=tail&&(f[team[tail]]>f[i]||(f[i]==f[team[tail]]&&a[i]>=a[team[tail]]))) tail--; tail++; team[tail]=i; } printf("%lld ",f[n]); } return 0; }
洛谷 P2564 [SCOI2009]生日礼物
题目描述
小西有一条很长的彩带,彩带上挂着各式各样的彩珠。已知彩珠有N个,分为K种。简单的说,可以将彩带考虑为x轴,每一个彩珠有一个对应的坐标(即位置)。某些坐标上可以没有彩珠,但多个彩珠也可以出现在同一个位置上。
小布生日快到了,于是小西打算剪一段彩带送给小布。为了让礼物彩带足够漂亮,小西希望这一段彩带中能包含所有种类的彩珠。同时,为了方便,小西希望这段彩带尽可能短,你能帮助小西计算这个最短的长度么?彩带的长度即为彩带开始位置到结束位置的位置差。
输入输出格式
输入格式:
第一行包含两个整数N, K,分别表示彩珠的总数以及种类数。接下来K行,每行第一个数为Ti,表示第i种彩珠的数目。接下来按升序给出Ti个非负整数,为这Ti个彩珠分别出现的位置。
输出格式:
输出应包含一行,为最短彩带长度。
深感不安,题解大佬都是o(N)的一遍扫描过,而我这个菜鸡只能想到n log n的二分,慌得一匹。
二分思路:这题答案满足单调性,所以我们就先排序(完了又一个n log n )然后直接二分答案。。。。。真的没啥好说的了

#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define re register using namespace std; struct node{ long long far,id; }a[1000001]; long long team[1000001],ans,n; long long o[101],head,tail,k,m,t; inline bool cmp(node c,node d){ return c.far<d.far; } inline char gc(){ static char now[1<<16],*S,*T; if(T==S){T=(S=now)+fread(now,1,1<<16,stdin);if (T==S) return EOF;} return *S++; } inline int read(){ int x=0,f=1;char ch=gc(); while(ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=gc();} while(ch<='9'&&ch>='0') x=x*10+ch-'0',ch=gc(); return x*f; } void write(int x){ if(x<10){putchar(x%10+48); return;} write(x/10); putchar(x%10+48); } inline bool check(long long x){ memset(o,0,sizeof(o)); head=1; tail=0; int g=0; for (re int i=1; i<=n; i++){ tail++; team[tail]=i; if (!o[a[i].id]) g++; o[a[i].id]++; while (head<=tail&&a[i].far-a[team[head]].far>x){ o[a[team[head]].id]--; if (!o[a[team[head]].id]) g--;head++; } if (g==k) return true; } return false; } int main(){ n=read(),k=read(); long long l=0,r=1e9,mid; // scanf("%lld%lld",&n,&k); for (re int i=1; i<=k; i++){ t=read(); //scanf("%lld",&t); while (t--){ m++; a[m].id=i; // scanf("%lld",&a[m].far); a[m].far=read(); } } sort(a+1,a+n+1,cmp); while (l<=r){ mid=l+r>>1; if (check(mid)) r=mid-1; else l=mid+1; } printf("%lld ",l); return 0; }
