归并排序（自顶向下、原地归并）

归并排序

归并排序是典型的分治思想的应用

归并排序大致分为以下几步骤：

首先要 “分“，假设有【8，4，5，7，1，3，6，2】数组，分的结果就是通过递归每次除2：[8,4,5,7,1,3,6,2]->【[8,4,5,7]和[1,3,6,2]】-->[8,4]、[5,7]，[1,3]、[6,2]只不过稍有不同的是，再分的过程中要进行排序再进行合并。

此时8,4进行排序，借助一个新数组，按顺序填入4，8；随后再放回原数组得：[4,8,5,7,1,3,6,2]

再是5,7排后[4,8,5,7,1,3,6,2]

再是4,8,5,7排序后[4,5,7,8,1,3,6,2]，此处就体现出了归并的思想；也是回溯的利用

以此类推排序1，3和6，2和1，3，2，6

最后再总体排一次:[4,5,7,8,1,2,3,6]，所有排序都是折半比较，如折半是8，则两边都已经是有序的了；接着交替比较两边就可得到。

这里的归并类似于深度优先中序遍历，如下图。

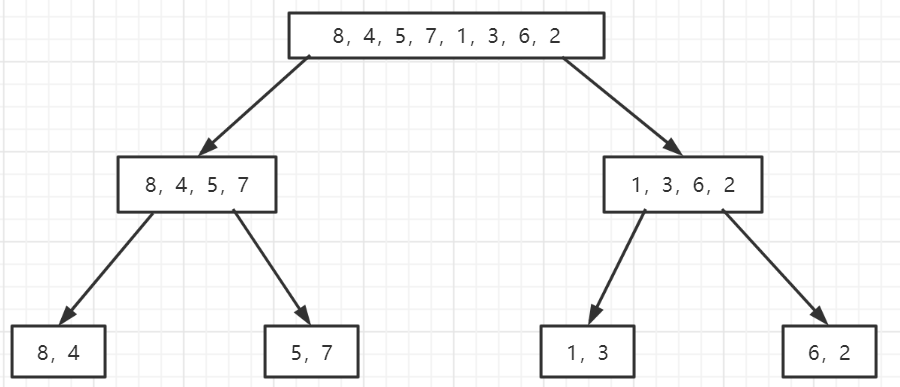
具体代码如下：

/*
nums:表示待排序的数组
left:切分后数组的起始索引
right:数组的右边界
temp:表示外排所需的空间
*/
public static void mergeSort(int[] nums, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (left + right)/ 2;
            mergeSort(nums, left, mid, temp);//递归每次mid左边所有的元素
            mergeSort(nums, mid + 1, right, temp);//每次mid右边的元素
            merge(nums, left, mid, right, temp);//排序
        }
    }

    public static void merge(int[] nums, int left, int mid, int right, int[] temp) {
        int l = left;
        int r = mid + 1;
        int i = 0;
//下面是排序过程
        while (l <= mid && r <= right) {
            if (nums[l] <= nums[r]) {
                temp[i] = nums[l];
                i++;
                l++;
            } else {
                temp[i] = nums[r];
                i++;
                r++;
            }
        }
  //下面是处理剩余的元素，如3,5,6,7,8;经过上面排序后，那么就直接将678赋到temp
        while (l <= mid) {
            temp[i] = nums[l];
            i++;
            l++;
        }
        while (r <= right) {
            temp[i] = nums[r];
            i++;
            r++;
        }
   //下面是将temp数组排好的元素，转移到原数组
        int leftTemp = left;
        i = 0;
        while (leftTemp <= right) {
            nums[leftTemp] = temp[i];
            i++;
            leftTemp++;
        }
    }

说明：

归并排序类似一个完全二叉树，而根据《算法》第四版给出的证明：归并排序是一种渐进最优的基于比较排序的算法；因为归并排序在最好和最坏情况下时间复杂度都为O(NlgN)，所以比较排序的上限和下限都是nlgn。但是具体情况则应另当别论，对于小型数组，也许选择或插入排序更快。而这些排序也都是基于比较的排序算法；也就是说除开比较，还有更优的无需比较的排序算法，况且归并排序的空间复杂度O(n)不是最优的。

所有随笔都是用作简单复习和参考而已，各位还是要看书或者系统学习，博客只是个人的一点点认知罢了。