LeetCode 树 98. 验证二叉搜索树（二叉搜索树，递归，中序遍历，迭代）

中序。

 刚拿到题目时，第一想法是递归，但是搞错了二叉搜索树成立的条件。

我以为的条件是：左侧树为二叉搜索树，右侧树为二叉搜索树，且root.right>root>root.left，然后递归。

但是显然这不对，满足以上条件后，root.right.left可能比root要小。

先说正确的递归解法：
正确的条件是：

• 左子树和右子树都是二叉搜索树
• root的值需要大于root左子树的所有值
• root的值需要小于root右子树的所有值

后两个条件可以转化为更好写代码的两个条件：

• 当前节点的值是其左子树的值的上界（最大值）
• 当前节点的值是其右子树的值的下界（最小值）

抽象为这个图

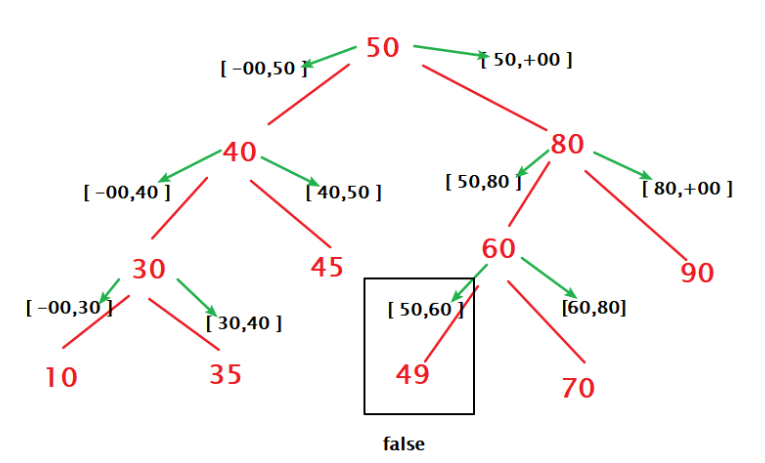
递归函数： helper(root,lower,upper)

递归函数的作用：以root为根节点的树，满足lower和upper的上下界限制

终止条件：1.当前节点时叶子节点，返回true 2.当前节点本身已经不满足[lower,upper]的上下界限制，返回false

递归关系：以root为根节点的树满足lower和upper的上下界要求的条件是：首先root得满足[lower,upper]的上下界限制，其次root.left需满足[lower,root.val]的上下界要求，且root.right满足[root.val,upper]的上下界要求

这个递归关系用语言描述起来感觉很模糊，但是对照着上一张图看起来就很清晰了。

class Solution {
  public boolean helper(TreeNode node, Integer lower, Integer upper) {
    if (node == null) return true;

    int val = node.val;
    if (lower!=null && val <= lower) return false;
    if (upper!=null && val >= upper) return false;

    if (! helper(node.right, val, upper)) return false;
    if (! helper(node.left, lower, val)) return false;
    return true;
  }

  public boolean isValidBST(TreeNode root) {
    return helper(root, null, null);
  }
}

代码有几处需要注意：

• 二叉搜索树是严格的，即root.left=root不可以，所以val = lower也要判定为false
• 初始条件时的上下界写什么。初始条件的意思是，第一个上下界不受限制，开始本来是准备写Integer.Max，但是发现有个测试用例真就是Integer.Max。所以最后采取这个null的写法，看到界为null，默认这个界不做判断。
• 条件中的与要用&&否则为null时一判断第二个条件就会报错。

所以这个解法真的好多坑啊。。。

下一种最容易看懂的方式，是以递归实现中序遍历，把二叉树的值中序遍历存到一个List里，然后检查这个List是否是升序的就行了

class Solution {
    List<Integer> res = new ArrayList<>();
    public boolean isValidBST(TreeNode root) {
        if(root==null)
            return true;
        inOrder(root);
        for(int i=1;i<res.size();i++){
            if(res.get(i)<=res.get(i-1)){
                return false;
            }
        }
        return true;
    }

    private void inOrder(TreeNode root){
        if(root!=null){
            inOrder(root.left);
            res.add(root.val);
            inOrder(root.right);
        }
    }
}

这种解法无比容易看懂，且时间复杂度是On，空间复杂度是On。但是当然还是要慢一些，如果直接通过迭代的方式实现中序遍历（压栈），就可以在遍历的过程中进行检测了。或者也可以通过递归的方式实现中序遍历，并在其中做判断：

class Solution {
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        // 访问左子树
        if (!isValidBST(root.left)) {
            return false;
        }
        // 访问当前节点：如果当前节点小于等于中序遍历的前一个节点，说明不满足BST，返回 false；否则继续遍历。
        if (root.val <= pre) {
            return false;
        }
        pre = root.val;
        // 访问右子树
        return isValidBST(root.right);
    }
}

这样很巧妙，但是更难理解一些。。。