双指针：42. 接雨水

 这题难度还是在想到办法，实现并不困难

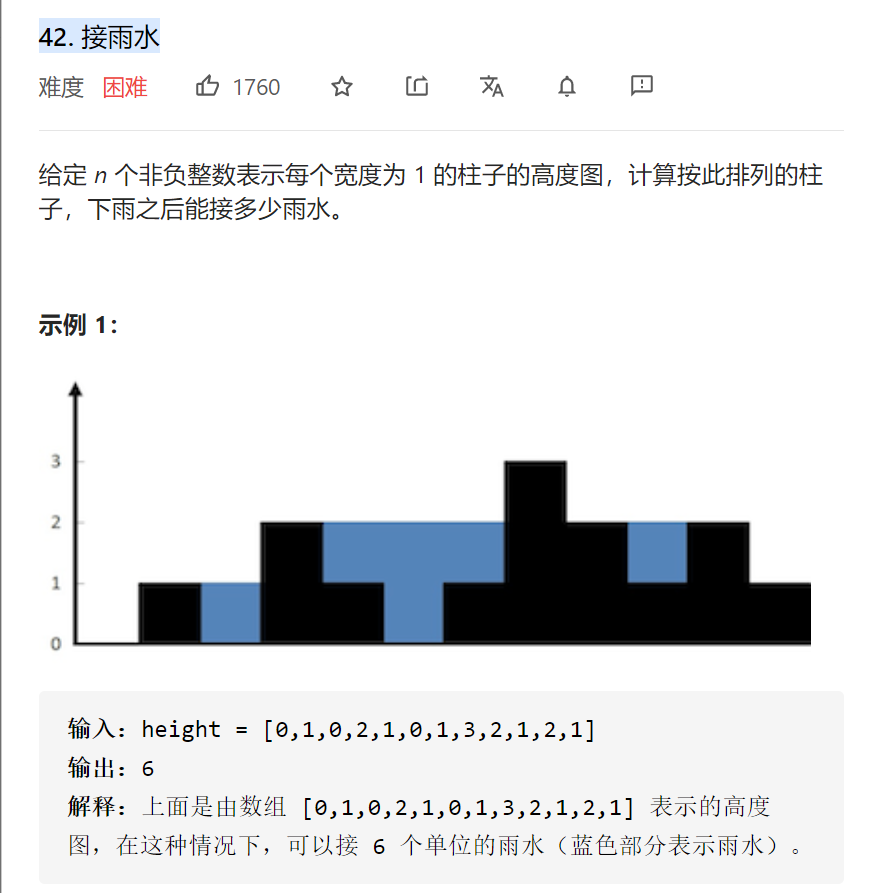
如何计算雨水呢，可以按列来算，统计每列能接的雨水

列的宽度已经确定了，能接雨水的高度等于

min（左侧最高的高度，右侧最高的高度）-本列高度

首先介绍双指针，左侧右侧靠扫描来计算

class Solution {
    public int trap(int[] height) {
        int result=0;
        for(int i=0;i<height.length;i++)
        {
            if(i==0||i==height.length-1)
            {continue;}
            int heightLeft=height[i],heightRight=height[i];
            for(int left=i;left>=0;left--)
            {
                if(height[left]>heightLeft)
                {
                    heightLeft=height[left];
                }
            }
            for(int right=i;right<height.length;right++)
            {
                if(height[right]>heightRight)
                {
                    heightRight=height[right];
                }
            }

            int h=Math.min(heightLeft,heightRight)-height[i];
            if(h>0)
            {result+=h;}

        }
        return result;
      }
}

由于第一列和最后一列肯定接不到雨水，所以直接为0

这样的时间复杂度是On2

还可以用动态规划来寻找左侧右侧，递推方程如下：

 这里需要注意边缘情况的maxLeft，要记住一个列的最小maxLeft就是height[i],这样意味着它是最高的，所以存不了水

class Solution {
    public int trap(int[] height) {
        int result=0;
        int[] maxLeft=new int[height.length];
        int[] maxRight=new int[height.length];
        for(int i=0;i<height.length;i++)
        {
            if(i==0)
            {maxLeft[i]=height[0];}
            else
            {
                maxLeft[i]=Math.max(height[i],maxLeft[i-1]);
            }
        }
        for(int i=height.length-1;i>=0;i--)
        {
            if(i==height.length-1)
            {maxRight[i]=height[i];}
            else
            {
                maxRight[i]=Math.max(height[i],maxRight[i+1]);
            }
        }
        for(int i=0;i<height.length;i++)
        {
            int h=Math.min(maxLeft[i],maxRight[i])-height[i];
            if(h>0)
            {result+=h;}
        }
        return result;
}
}

本题还有一种解法叫单调帧法，可以在O1的空间复杂度和On的复杂度完成这道题