SPFA是高效的最短路算法中最容易理解的一个(实际上也就是SPFA和Dijkstra俩个)
嗯嗯来看看吧,虽然SPFA是题目最喜欢卡的算法:
算法介绍:
SPFA实际上是Bellman-Ford的优化,原理跟Bellman-Ford是一样的,即松弛操作(可以点击上面链接回顾,SPFA的主要优点就在于它优化了Bellman-Ford的遍历过程。Bellman-Ford遍历是简单粗暴的,就是考虑最坏情况暴力地循环,但是SPFA在遍历过程中即可以看出什么时候该停止循环,什么时候不该停止循环,这就需要队列来实现。
遍历过程
SPFA遍历过程比较难懂(当然这也是SPFA的精髓所在),下面是其中的过程:
首先建一个队列让元素排队入场。那么第一个入队的是起点(我们将它标记为 (A) 点)。我们以这个 (A) 点为中心,对与此点相连的所有点进行松弛操作。只要碰到有过改变的点就让改变了的点拖去排队
等待劳改,譬如一开始将 (A) 相连的 (BCD) 三点的值从(INF)改成了一个具体数值,那么这些个被改变的坏小孩(点(BCD))就需要被送到队尾然后送去劳改班。在进行了一次松弛操作后,(A) 点成功从劳改班毕业,出队。然后对于每个在队列里的元素都进行对于与它相连的点的松弛操作,即重复地把队伍里的元素进行劳动改造,同时揪出与这个点相连的那些被改变的点然后再取到队伍后面。只要队列为空即搜索完成。总结一下:
举个栗子:
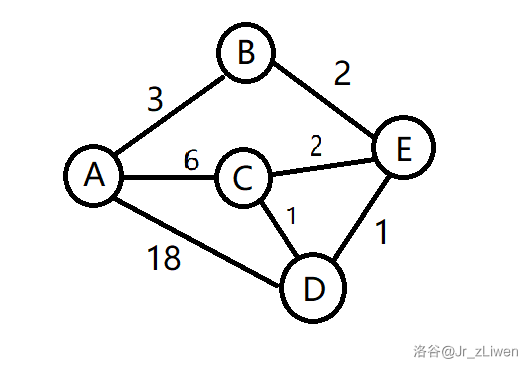
对于这个图我们首先把 (A) 入队,第一次松弛改变了 (BCD) 的值,然后把 (A) 踢出去。那么很显然,现在
然后我们让 (BCD) 入队,首先找 (B) ,与其相连的点为 (AE),很显然 (E) 肯定会被改变,而 (A) 现在不需要松弛,因为 (A=0),而(B+edge_{AB}=3+3=6),或者说本来 (B) 就是从 (A) 来的自然不用走回头路。于是我们再把 (B) 踢出队列,把 (E) 入队(因为只有它被改变了值)。那么很显然,现在:
然后讨论现在队头的 (C),我们需要讨论的是 (CDE),进行松弛计算后,我们发现 (E) 的值还差(1)才值得被改变,不管它(其实为了省时间我们最好用 (<) 而不是 (leq),即当有相等的时候不用再次入队)。接着我们就发现很开心的事情,(D) 的值可以被改变,但是我们不用把 (D) 再次放到队尾(注意:如果 (E) 搜完以后改变了 (C),我们自然还会再次搜索 (C),而不是理解为搜完E更新后还要再搜 (D))所以我们需要一个数组来判断每个点是否存在于队列中,。同理可得,(A) 被排除。那么很显然,现在:
同理可得,我们继续遍历接下来的点,接下来的过程就简单了:
1.查找D,啥都没更新,D出队;
2.查找E,更新 D=E+edge[E][D]=5+1=6,其他不更新;
3.查找D,啥都没更新,D出队,队列为空。
最后我们的出了最优解:
代码
栗子举完了就上代码了(简单粗暴):
#include<bits/stdc++.h>
#define N 1000001
#define INF 0x7fffffff
using namespace std;
bool iqueue[N];//判断是否在队列中 (is_in_queue)
int dis[N];//记录点的值
struct node
{
int des,val;
}tmp;//给结构体亿个差评
vector <node>spfa[N];//给优先队列亿个好评
queue<int> q;//再给普通队列亿个好评
int main()
{
int dotNum,edgeNum,origin;
scanf("%d%d%d",&dotNum,&edgeNum,&origin);
for(int i=1;i<=edgeNum;++i)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
tmp.des=v;tmp.val=w;
spfa[u].push_back(tmp);
}
q.push(origin);
iqueue[origin]=true;
for(int i=1;i<=dotNum;++i)
{
dis[i]=INF;
}//初始化点的数据
dis[origin]=0;
int u,v,len;
while(!q.empty())
{
u=q.front();q.pop();
len=spfa[u].size();
for(int i=0;i<len;++i)
{
v=spfa[u][i].des;
if(dis[u]+spfa[u][i].val<dis[v])
{
dis[v]=dis[u]+spfa[u][i].val;
if(!iqueue[v])
{
q.push(v);
iqueue[v]=true;
}
}
}
iqueue[u]=false;
}
for(int i=1;i<=dotNum;++i)
{
if(i==origin)
{
cout<<"0 ";
}
else
{
cout<<dis[i]<<' ';
}
}
return 0;
}
SPFA完成了!!!接下来要打重点的Dijkstra了QAQ。。。
填坑第 (huge{3}) 站完成!!!