数学期望(ξ) 浅析

前言：为初赛而奋斗！！！

谨以此系列祝愿我通过CSP-J初赛QwQ

正文：期望是什么？

我们先说一下期望(符号是(xi)，在经过百度以后，我们发现一个定义：

[small{ ext{数学期望是试验中每次可能结果的概率乘以其结果的总和}} ]

[Large{ ext{举个栗子}} ]

小明在银行存了100元定期，利率是(2\%)。我们知道，定期几乎没有风险，那么期望代表的就是小明从这个定期存款种所希望得到的利息。那么这个期望怎么算呢？由于没有风险，所以得到的概率是(100\%)。也就是说小明从定期所预计得到的利息就是:

[xi=100\% imes 2\% imes 100 ext{元}=2 ext{元} ]

由于小明很有钱,他又买了(100)元的股票。(70\%)赚(10\%)，(30\%)亏(5\%)，那么他期望得到的钱数是：

[ ext{可能盈利部分: } xi_1=70\% imes 10\% imes 100 ext{元}= 7 ext{元} ]

[ ext{可能亏损部分: } xi_2=30\% imes (-5\%) imes 100 ext{元}= -0.3 ext{元} ]

[ ext{最后期望收益: } xi_{ ext{总}}=7 ext{元}+(-0.3) ext{元}=6.3 ext{元} ]

这么看来期望是很好理解的，实际上就是帮助你预算自己的收益，那么接下来我们捉(2)只初赛题来看看：

第一题

[Large{noip_{2013} ext{提高组}t_{22}} ]

首先我们看完题，你可能会觉得有一点难以理解。首先我们先要读懂题，下面讲为您分点解释：

1、青蛙可能傻傻地原地不动

题目中又说：“青蛙再(k)点可能等概率地跳到(1)_{$k$号荷叶上”。那么它每次都有$dfrac{1}{k}$的概率跳到$1$}(k)任意一点上。那么会发现它竟然很有可能站在原地不动啊。那么这个概率的计算就很恶心人了，小学数学并不能告诉我这种奇葩的概率应该怎么计算。这时需要记住一点：它要求的是平均次数。在平均次数中，青蛙确实有可能原地不动并跳上无数次，但是每次它都只有(dfrac{1}{k})的概率跳回(k)点。而我们不能考虑它原地不动所造成的影响。但是，因为越往后发展青蛙一直不动的概率就越小，小到可以忽略不记，所以就基本不需考虑了。那么"平均次数"到底怎么算呢（加和取平均值？(∞)咋办？？），且听下面分解。

2、平均次数的计算：期望值相加

既然我们讲到期望，那么这里的分析就肯定不止是一个方法啦。我们已经知道了期望值的定义，那么这里所谓的“平均次数”就可以转换为青蛙期望自己跳回(1)所需次数。我们知道青蛙有很多条路径可以跳回(1)，而这里总的期望值即为这些路径的期望值的和。比如青蛙可以[(5)-->(3)-->(1)]跳(2)次到达，而这种跳法的概率是(dfrac{1}{5} imes dfrac{1}{3}=dfrac{1}{15}),也就是说这种跳法的期望值是(dfrac{1}{15} imes2 ext{次}=dfrac{2}{15} ext{次})。而经过[(5)-->(5)-->(5)-->(4)-->(1)]跳(4)次到达的期望值也就是((dfrac{1}{5})^3 imesdfrac{1}{4} imes4 ext{次}=dfrac{1}{125} ext{次})。

引述：那么由此我们也可以解决上面的第 1个问题，当原地跳的概率无限接近于 0时，期望值也就是 0了。

然后，虽然我们已经知道了原理。但是我们还是不会计算——因为有无数条路径，无数个排列组合，该怎么办呢？如果拥有一点递推的思想就再好不过了。

1. 设(xi_x)表示从(x)号荷叶跳到(1)号荷叶的期望值

2. 显而易见，(xi_1=0)（无论如何都只用跳0次);

3. (xi_2=dfrac{1}{2} imes(1+xi_2)+dfrac{1}{2} imes(1+xi_1))（无论往哪跳都要跳(1)次才到目的地）

4. (xi_3= dfrac{1}{3} imes (1+xi_3)+dfrac{1}{3} imes(1+xi_2)+dfrac{1}{3} imes(1+xi_1))（同上哦）

。。。。。。

5. 由此可得：(xi_n=sum_{i=1}^{n}[dfrac{1}{n} imes (1+f_i)])

6. 代入(n=5):

[xi_5= dfrac{1}{5} (1+xi_5)+dfrac{1}{5} (1+xi_4)+dfrac{1}{5}(1+xi_3)+dfrac{1}{5}(1+xi_2)+dfrac{1}{5}(1+xi_1) ]

7. 化简上面式子并通过(xi_1=0)推上来即可算出这只死青蛙从(5)跳到(1)的平均次数即为(dfrac{37}{12})。

第二题

[Large{noip_{2018} ext{提高组}t_{7}} ]

在一条长度为 1 的线段上随机取两个点，
则以这两个点为端点的线段的期望长度是_____

分析问题

其实这题本来是选择题，很容易猜出就是(dfrac{1}{3})，但是我们还是要证明的。我们再次重申：期望长度即对于所有情况其发生的概率( imes)这种情况下线段的长度。那么进一步分析，由于一条线段上有无数个点，概率就变成了(dfrac{1}{∞})，不过看到无穷个点不知你是否想起了穷竭法呢？——那就是可以用积分来求了！我们先说结论，再说思路（这已经是我能找到最容易理解的方法了）

[sum_{m=1}^{n}dfrac{dfrac{m}{n-1} imes(n-m) imes 2}{n^2} ]

具体思路

1. 首先把一条线段平均分成(n-1)份，设这两个点只会出现在(n)等分点上。

2. 由于选择(1)个点的概率是(dfrac{1}{n})，那么选择(2)个点的概率即(dfrac{1}{n^2})

3. 对于每一种情况，设其长度为(L)，也就有概率( imes)结果(=dfrac{L}{n^2})

4. 设(L)取了(q)份((1)份为(i)号点和(i-1)号点的距离)，所以(L=dfrac{1}{n-1} imes q=dfrac{q}{n-1})

5. 由于取了(q)份，那么长度为(L)的情况就有((n-q))份,那么对于每一个(q)值的期望我们可以用(dfrac{dfrac{q}{n-1} imes (n-q)}{n^2})来表示

6. 但是不要忘记，由于两个点的顺序没有确定，所以结果还要( imes 2)（这里也可以理解为在数轴上(1)号点可以在(2)号点的两侧，这里的距离就是(|x_1-x_2|)也就是当线段长度为(L)，且已知他们能够匹配42个值时，(x_1)和(x_2)的顺序时不确定的，所以有(x_1>x_2)、(x_1<x_2)两种情况，所以在原来期望值的基础上要( imes 2)）,那么最后：

[xi=dfrac{dfrac{q}{n-1} imes (n-q)}{n^2} imes 2 =dfrac{dfrac{q}{n-1} imes(n-q) imes 2}{n^2} ]

7. 把所有的(q)罗列出来期望值加和即为线段的期望长度了，也就最后得到了上面的式子！！！（即(q=1,2,3...n)的期望值总和）

增进理解

如果觉得上面说的比较抽象，可以看看具体的例子，其实效果最好的就是手动模拟，自己找个(n)值带进去算一下就好了，你会发现每一次都有一点误差，毕竟没有达到无穷。

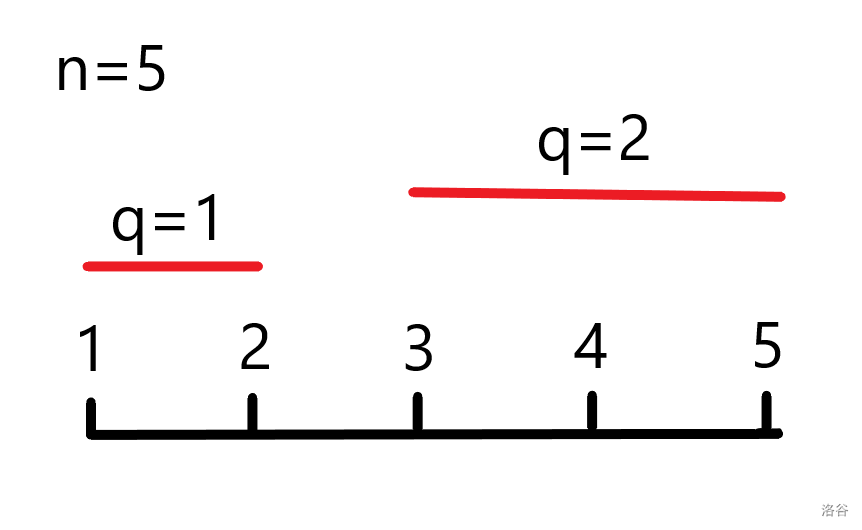
对于上面那个图来说，很容易看出：

1. (q=1)时有([1,2][2,3][3,4][4,5])共(4)条线段满足条件（当然还有([2,1][3,2][4,3][5,4])是潜在的，所以总共(4 imes 2=8 ext{条})），而每一种情况发生的概率均为(dfrac{1}{25})，而且长度皆为(dfrac{1}{4}),那么(q=1)的期望值为(xi_1=dfrac{8 imes dfrac{1}{4}}{25}=dfrac{2}{25})，

2. 那么(q=2)时：(xi_2=dfrac{dfrac{1}{2} imes 6}{25}=dfrac{3}{25})

3. (q=3)时： (xi_3=dfrac{dfrac{3}{4} imes 4}{25}=dfrac{3}{25})

4. (q=4)时： (xi_4=dfrac{1 imes 2}{25}=dfrac{2}{25})

5. 那么期望值的总值就有:(xi=q1+q2+q3+q4=dfrac{10}{25}=dfrac{2}{5})

这里期望值0.4距离0.333确实有比较大的差距，但这是因为(n)较小，你可以尝试推一下更大的(n),你就能发现期望值越来越接近(dfrac{1}{3})了。

计算问题

[sum_{m=1}^{n}dfrac{dfrac{m}{n-1} imes(n-m) imes 2}{n^2} ]

想必你一定对它的计算充满了恶心，所以演示一遍如何解决它。下给出用到的公式（如果做到这份上你还看不懂过程就真的时代的眼泪了）：

[1+2+3+4+...+(n-1)+n=dfrac{n(n+1)}{2} ]

[1^2+2^2+3^2+...+(n-1)^2+n^2=dfrac{n(n+1)(2n+1)}{6} ]

---

---

[large ext{1、平方和公式的简单证明：} ]

---

---

解：(∵ ext{对于任意的n,有：}n^2=n(n+1)-n)

(∵ ext{有：}n(n+1)=dfrac{1}{3}[n(n+1)(n+2)-n(n-1)(n+1)])

(∴n^2=dfrac{1}{3}[n(n+1)(n+2)-n(n-1)(n+1)]-n)

( iny{sum^n_{i=1}i(i+1)=dfrac{1}{3}(n(n+1)(n+2)-n(n-1)(n+1)+n(n-1)(n+1)-n(n-1)(n-2)+n(n-1)(n-2)-...+1 imes2 imes3-0)})

( ext{(这就是个裂项，非常开心地把中间全部消掉)})

(=dfrac{1}{3}[n(n+1)(n+2)-0]=dfrac{1}{3}n(n+1)(n+2))

(∵ ext{原式}=n^2+(n-1)^2+...3^2+2^2+1^2)

( iny{=n(n+1)-n+(n-1)(n-1+1)-(n-1)+(n-2)(n-2+1)-(n-2)+...+2 imes3-2+1 imes2-1})

(=sum^n_{i=1}i(i+1)-sum^{n}_{i=1}i iny ext{ 即}(=sum^n_{i=1}i^2))

(=dfrac{1}3n(n+1)(n+2)-dfrac{n(n+1)}{2} iny ext{(等差数列公式)})

(=dfrac{2n(n+1)(n+2)-3n(n+1)}{6}=dfrac{n(n+1)[2(n+2)-3]}{6})

(=dfrac{n(n+1)(2n+1)}{6})

---

---

[large ext{2、然后开始漫长的解题过程QAQ:} ]

---

---

解：原式(=frac{frac{1}{n-1} imes(n-1) imes 2}{n^2}+frac{frac{2}{n-1} imes(n-2) imes 2}{n^2}+frac{frac{3}{n-1} imes(n-3) imes 2}{n^2}+...+frac{frac{n}{n-1} imes(n-n) imes 2}{n^2})

(=dfrac{2 imes[(n-1)+2(n-2)+3(n-3)+...+n(n-n)]}{n^2 imes(n-1)})

(=dfrac{2 imes[n-1^2+2n-2^2+3n-3^2+...+n imes n-n^2]}{n^2 imes(n-1)})

(=dfrac{2 imes[(1+2+...+n)n-(1^2+2^2+...+n^2)]}{n^2 imes(n-1)})

(=dfrac{2 imes[dfrac{n(n+1)}{2} imes n-dfrac{n(n+1)(2n+1)}{6}]}{n^2 imes(n-1)})

(=dfrac{n^3-n}{3 imes n^2 imes(n-1)} iny{ ext{(上面的式子你肯定能化简，自己慢慢推吧)}})

(=dfrac{n imes(n^2-1)}{3 imes n^2 imes (n-1)}=dfrac{n imes (n-1) imes (n+1)}{3 imes n^2 imes(n-1)})

(=dfrac{n imes(n+1)}{3n^2}=dfrac{n^2+n}{3n^2}=dfrac{1}{3}+dfrac{1}{3n} iny{ ext{(终于啊！QAQ)}})

此时由于 (n o ∞) 那么 (dfrac{1}{3n} o 0) 可以忽略不计(取值为0)，那么答案即为 (dfrac{1}{3})

然后你还会发现，前面 (n=5) 时与正确答案的差距恰好是(dfrac{2}{5}-dfrac{1}{3}=dfrac{1}{15}=dfrac{1}{3 imes5})，即(dfrac{1}{3n})

总结：

期望很恶心，很多时候当所需的期望值变得很多的时候就不像文章开头小明买股票的例子那么简单了。就算你成为了时代的眼泪，你也需要继续努力哦！！！

[Huge{ ext{咕咕咕}} ]