树状数组 算法分析

一个神奇的稀奇古怪的算法

算法优劣：

树状数组是用来维护区间的，应该是做区间问题时最常用的方法了（除了暴力）。树状数组的优点很明显：与线段树相比码量小，空间小，容易调试 ，与分块相比易理解，更快捷。然而缺点也是很致命的：它能做的事不多，一般都只是用来查找区间和、区间极值等问题。更复杂的区间维护就用不了树状数组了QAQ。

---

---

---

---

---

所谓“树状数组”：

——树状数组最良心的地方就在于它是线性的！只要用一个一维数组存储就行了。

——线段树不也是吗  -_-

——啊这，线段树查询很麻烦嘛。。。

如何用一个线性的数组当作树来用呢？这是线段树、堆、树状数组这一类算法所要研究的问题。在线段树和堆中，我们所用的方法就是左节点p<<1,右节点p<<1|1 。而在树状数组中，有一个非常玄学奇妙的算法——(lowbit)，为了方便解释，下面上图：

[ ext{令原数组为C，树状数组为T。} ]

[T_1=C_1 ]

[T_2=C_1+C_2 ]

[T_3=C_3 ]

[T_4=C_1+C_2+C_3+C_4 ]

[T_5=C_5 ]

[T_6=C_5+C_6 ]

[T_7=C_7 ]

[T_8=C_1+C_2+C_3+C_4+C_5+C_6+C_7+C_8 ]

[T_9=C_9 ]

[T_{10}=C_9+C_{10} ]

[ ext{以此类推。。。。。。} ]

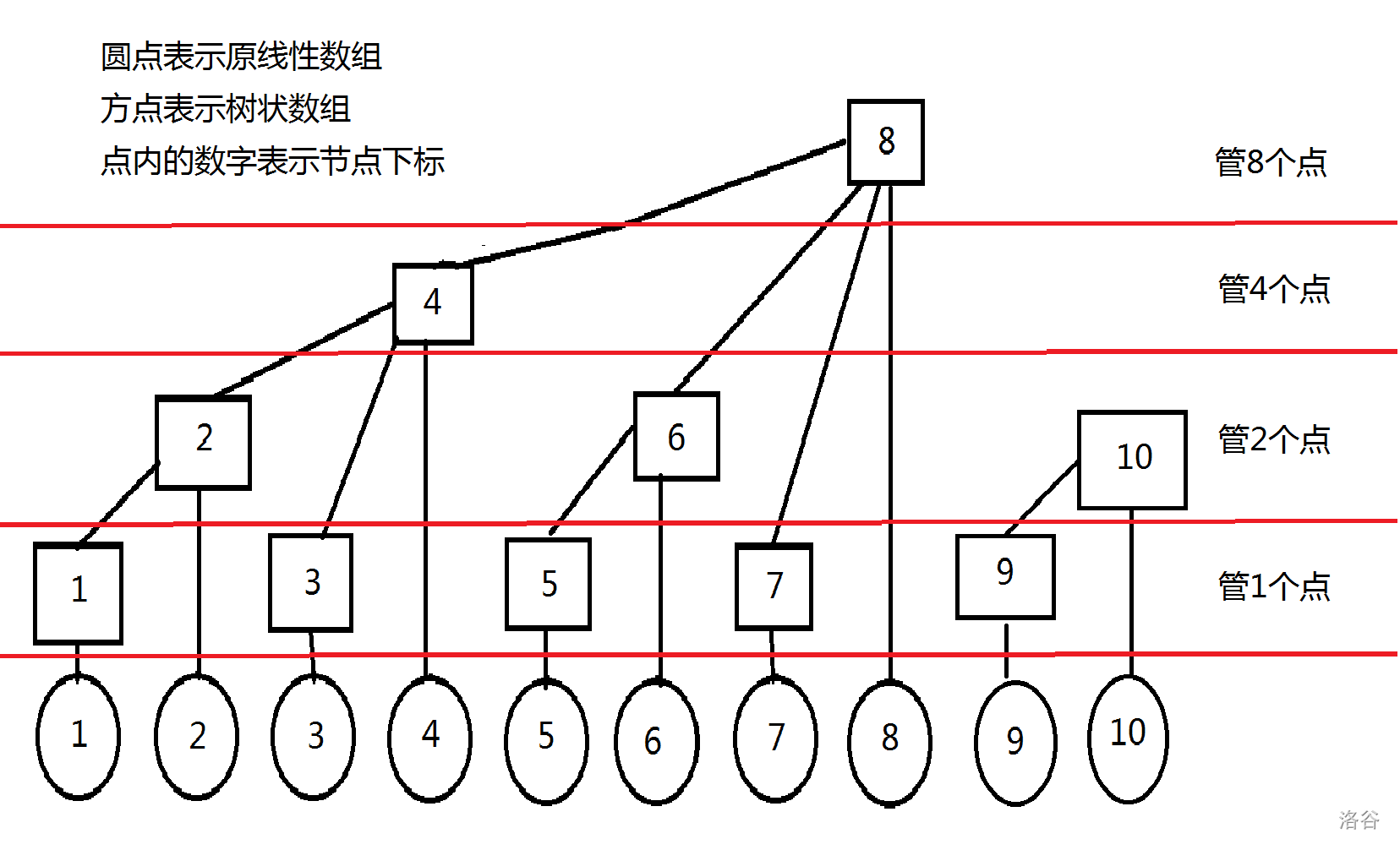
这应该很容易发现规律，但是。。。如何把规律表示成式子就是个很恶心的问题，那么免去推理过程，有：

[T_n= sum^{n-2^k+2^k( ext{即}n)}_{i=n-2^k+1}C_ismall ext{ -------->k为n在2进制下末尾0的个数} ]

或者说的形象一点，比如(n=6)时，(6) 所能够整除的最大的的 (2) 的次方数为 (2) ，(2=2^1), 因此:

[T_6=C_{6-2^1+1}+C_{6-2^2+2}=C_5+C_6 ]

• 注：求(2^k)的操作名为lowbit

(large ext{那么以上就是树状数组的存储规则})

算法实现：

[Large ext{引：计算}2^k ext{值(lowbit)} ]

上面已经明确k为n在2进制下末尾1的个数，这个(1)的个数我们可以用 n&(-n) 去查找，证明下面给出，至于怎么想到的。。。。。。因为我们的前辈是有大智慧的人

众所周知， -n即为n取反加(1)。如果不加(1)，那么很容易发现n的反码 & n的原码 = 0000000.....0。那么n&(-n)的大小就决定在这个加的(1)上。那么因为取反以后，前面所有的(0)都变成了(1)，加上 (1) 就会发生进位，那么进位一直持续到遇见第一个 (0)，即原来的第一个 (1) 的位置上，并且在进位的途中所遇到的所有 (1) 全部都变成 (0)。那么也就是说，除了最后停下来的那个被变成 (1) 的 (0) 的位置上是 (2) 个 (1)，其他的所有位置上都有 (0)，那么进行&操作的时候就会全部变成0，那么最后得出的结果就是1后面跟着k个0，那也就是(2^k)了

[Large ext{1、修改节点} ]

树状数组一般只能是修改单点（这就体现出与线段树的差距了）。那么既然是修改单点（假设要修改 (n)），我们就要找到所有存有(C_n)的 (T_i)，并将所有的 (T_i) 更新。那么我们就要找到 (n=i-2^k+b(1leq b leq 2^k))。一个T节点的上一级肯定是(2^{k+1})，因为它的上级必然会管到(j-2^{k_1}+1)，也就是管了(2^k)个点，而它所直接管辖的(T)节点的管辖个数必然是(2^{k_1-1})，那么所以应该很容易看出，只要依次向上加一个(2^ksmall ext{（这个k随节点变化而变化）})，一直加到数组上限就能找到所有管着(C_n)的点了。那么代码实现就很简单了：

inline void addNum(int p,int v)
//给p节点加上v
{

    while(p<=n)
    {
        t[p]+=v;
        p+=(p&(-p));
    }
    return;

}

[Large ext{2、查询区间答案} ]

因为树状数组的存储信息不多。所以只能退而求次。比如要求([l,r])的和，那么我们就可以去用([1,r]-[1,l-1])这样求前缀和的形式来把([l,r])求出来。那么此时，我们就需要找到能够拼凑成类似([1,n])的和的节点并加和。去观察一下图像，很容易发现([1,8])即为(T_8)的值，([1,7])也很好找，是(T_7+T_6+T_4)。进一步发现它的规律，我们发现，当我们寻找([1,n])时，首先(T_n)必然是会被包括的（如果加了(T_i(i>n))，必然会有多余的值被包含，而如果只加了(T_i(i<n)),则(n)也不可能被包括）。然后我们就可以堂而皇之的将(T_n)加进去了。当我们把(T_n)加进去以后，那么(T_n)所包含的最小的(C_i)的(i)值就是(small{i-2^k+1})(上面讲的规律)，那么现在的问题就转换成了求([1,n-2^k])了.所以我们要求的就肯定含有(T_{n-2^k})了，通过这样，我们就可以进行操作直到(small{n-2^k=0})。

inline int getAns(int p)
//寻找 [1,p] 的和 
{
	int ans=0;
	while(p)
    {
        ans+=t[p];
        p-=(p&(-p));
    }
    return ans;
}

代码汇总

• 1. 方便您调试的代码（显示一个树状数组结构）

#include<bits/stdc++.h>
#define lb(a) (a&(-a))
using namespace std;
int main()
{
	cout<<"输入树状数组范围："; 
	int n;cin>>n;
	for(int i=1;i<=n;++i)
	{
		cout<<"对于节点 "<<i<<" 有："<<endl<<"T"<<i<<" = ";
		for(int j=i-(lb(i))+1;j<i;++j)
		{
			cout<<"C"<<j<<" + ";
		}
		cout<<"C"<<i<<endl;
		cout<<"(2^k)lowbit("<<i<<") = "<<lb(i)<<endl<<endl<<endl;
	}
	return 0;
}

• 2. 树状数组代码（模板第1题）

#include<bits/stdc++.h>
#define lb(w) (w&(-w))
using namespace std;
int t[500001],n;
inline long long int read()
{
	long long int res=0;bool flag=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')flag=0;ch=getchar();}
	while(ch>='0'&&ch<='9'){res=(res<<1)+(res<<3)+(ch^48);ch=getchar();}
	if(flag)return res;return -res;
}
inline void addNum(int p,int v)
{
    while(p<=n)t[p]+=v,p+=lb(p);
    return;
}
inline int getAns(int p)
{
	int ans=0;
	while(p)ans+=t[p],p-=lb(p);
	return ans;
}
int main()
{
	n=read();int m=read();
	for(int i=1;i<=n;++i)
	{
		int r=read();
		addNum(i,r);
	}
	for(int i=1;i<=m;++i)
	{
		int o=read(),x=read(),y=read();
		if(o==1)addNum(x,y);
		else
		{
			int ans=getAns(y)-getAns(x-1);
			printf("%d
",ans);
		}		
	}
	return 0;
}

配套算法 线段树 ------>