Tarjan 算法小结

I. 简介

Tarjan (音: 塔扬) 是个神犇，他发明了图论中的著名算法 tarjan 算法

可以轻松方便地解决 (2) 种图的连通性问题——割点/边(Cut)与强连通分量(SCC)

割点/边用来解决一些针对性的图的连通问题，强连通分量则广泛运用于化图为 (DAG) (缩点) 、(2-SAT) 问题。

（注：不严谨地注明一下，割点/边用于无向图，缩点用于有向图（缩点不能求无向图最大团喔）)

---

II. 总思想：

定义

tarjan 算法的精髓在于 (2) 个数组：dfn 和 low 。

dfn 是该节点的 dfs序 编号 ，俗称时间戳，指它被遍历到的时刻。

low 比较魔性，表示从该节点出发，通过非父子关系的边能回到的最早的节点。

（感谢图论神器）例如下面这张图：

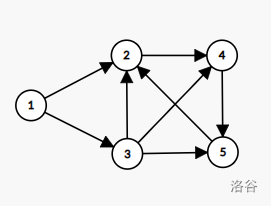
(数据不唯一，下面以遍历顺序：(1,2,4,5,3) 为例，数组下标由 (1) 开始编号):

(large{dfn={1,2,5,3,4}})

(large{low={1,2,2,2,2}})

（例如 (4) 节点可以通过 (4,5,2) 回到时间戳为 (2) 的 (2) 节点，所以low[4]=2

有了这 (2) 个数组的定义我们就可以进行奇怪的操作，不过还是先看看它们怎么求。

思路实现

dfn 很容易求，记下遍历时间即可知道。

low 实际上是利用回溯能够快速算出的一个量，主要步骤如下：

1. low 的初始值为 dfn (指向自己)

2. 当前节点有一条非通向其父亲的路径指向其某一个祖先，则更新 low 值。

3. 如果它的儿子能够通向更早的节点，将 low 值更新为它儿子的 low 值。

---

III. 割点/割边 (Cut)

定义

• 割点：如果去掉某个点以及与这个点相连的所有边，整个图被分为多个不为空的连通块，则这个点是割点。

• 割边：如果去掉某条单独的边，整个图被分为多个不为空的连通块，则这条边是割边。

求法

设想一棵 dfs 树，考虑如果某一结点 (u) 的儿子能够回到这一结点的祖先节点，说明即使删掉 (u) 也不能阻挡 (u) 的儿子与它祖先的连通。

那么，如果结点 (u) 的儿子不能回到这一节点的祖先，那么很明显，没有 (u) 则它的儿子就回不去了 QAQ 。

那么很明显，求取的方法是 ( (v) 节点是 (u) 节点的儿子 )： IF(low[v]>=dfn[u])u为割点，边 (u,v) 为割边;

同时，根节点需要特判，若它有 (>1) 个儿子它才是割点（可能会是删了根节点以后出现 (1) 个连通块和 (1) 个空的点集）

void tarjan(int u)
{
	t[u].low=t[u].dfn=++dep;for(int i=a.head[u];i;i=a.nxt[i])
	{
		int v=a.des[i];if(!t[v].dfn)
		{
			tarjan(v);t[u].low=min(t[u].low,t[v].low);
			if(t[u].dfn<=t[v].low&&u!=Rt)t[u].isc=1;ch+=(u==Rt);
		}
		t[u].low=min(t[u].low,t[v].dfn);
	}
}
int main(){input();for(int i=1;i<=n;++i){if(!t[i].dfn){dep=0;dfs(i);if(ch>1)t[i].isc=1;}}}

---

IV. 缩点 ——求强连通分量(SCC)

定义

• 强连通分量(以下简称 SCC )：有向图中两两之间能够互相到达的点集。如最经典的三角强连通(口胡的名字)： 。

求法

再次想象一棵 dfs 树，考虑如果一个点 (u) 可以通过 (u) 的儿子用不同的路回到 (u) ，则证明只要走对了路，有一串点是可以重复到达的，也就是它们形成了 SCC 。而又由与 low 的值在这棵树上是单调的，所以当 low==dfn时，从某一子节点到 (u) 的一串点一定是在最大的一个 SCC 中(即不会出现包含的情况)，所以只需要每次对 dfn==low 的点进行一次标记即可。

具体来说，每次将点压入栈中，碰到 dfn[u]==low[u] 者则证明栈里面的点同在 (1) 个 SCC 中，并将它们弹出避免对后续造成影响。

void tarjan(int u)
{
	t[u].dfn=t[u].low=++dep;iss[stk[++top]=u]=1;
	for(int i=a.head[u];i;i=a.nxt[i])
	{
		int v=a.des[i];if(!t[v].dfn)tarjan(v),t[u].low=min(t[u].low,t[v].low);
		else if(iss[v])t[u].low=min(t[u].low,t[v].dfn);
	}
	if(t[u].dfn==t[u].low){int v;cnt++;do{iss[v=stk[top--]]=0;t[v].scc=cnt;}while(v!=u);}
}

这样我们就将点染好色，然后操作一下就能实现将普通有向图变成一个 (DAG) 啦！

---

V. 2-SAT 问题

定义：有很多节点和节点间的逻辑关系（一个节点非 (1) 即 (0)），但这些逻辑关系均满足尽有 (2) 项是关联的，给每个点赋值(0/1)构造一个满足要求的条件。

其实吧，这个应该多开一个 blog 来讲的，不过博主又懒又烂。

对每一个节点建立正反节点，(u) 正结点表示条件 val[u]==true ,反节点表示条件 val[u]=false （下面写作 (U) 和 (!U)）。

每次得到逻辑关系形如："若 (A) 则 (B) " 时，建立边 ((A,B)) 以及 ((!A,!B)) 。表示若某一结点所包含条件为真，则其指向的节点所包含条件为真。

可以发现， (U) 与 (!U) 不可能同时满足，所以当 (U) 与 (!U) 处于同一个 SCC 中时，该题无解。

否则，我们可以发现，拓扑序越后，所影响的节点越少，所以很容易证明在有解情况下 (u) 结点的取值为 (U) 和 (!U) 中拓扑序靠后的一个。

代码(洛谷模板):

#include<bits/stdc++.h>
#define rep(a,b,c) for(int c=(a);c<=(b);++c)
#define drep(a,b,c) for(int c=(a);c>=(b);--c)
#define grep(a,b,c) for(int c=a.head[(b)];c;c=a.nxt[c])
using namespace std;
const int N=2e6+5,M=2e6+5,INF=0x3f3f3f3f;
struct Graph{int des[M],nxt[M],head[M],cnt;inline void ins(int x,int y){des[++cnt]=y;nxt[cnt]=head[x];head[x]=cnt;}}a;
struct Tarjan{int low,dfn,scc;}t[N];int stk[N],top,dep,cnt,n,m;bool iss[N];
inline int read()
{
	int res=0;char ch=getchar();bool flag=0;
	while(ch<'0'||ch>'9')flag=(ch=='-'),ch=getchar();
	while(ch<='9'&&ch>='0')res=res*10+(ch^48),ch=getchar();
	return flag ? -res : res ;
}
void tarjan(int u)
{
	t[u].dfn=t[u].low=++dep;iss[stk[++top]=u]=1;grep(a,u,i)
	{
		int v=a.des[i];if(!t[v].dfn)tarjan(v),t[u].low=min(t[u].low,t[v].low);
		else if(iss[v])t[u].low=min(t[u].low,t[v].dfn);
	} if(t[u].dfn==t[u].low){int v;++cnt;do{iss[v=stk[top--]]=0;t[v].scc=cnt;}while(v!=u);}
}
int main()
{
	int n=read(),m=read();rep(1,m,i)
	{
		int a1=read(),b1=read(),a2=read(),b2=read();
		if(!b1&&!b2){a.ins(a1+n,a2);a.ins(a2+n,a1);}
		if(b1&&!b2){a.ins(a1,a2);a.ins(a2+n,a1+n);}
		if(!b1&&b2){a.ins(a1+n,a2+n);a.ins(a2,a1);}
		if(b1&&b2){a.ins(a1,a2+n);a.ins(a2,a1+n);}
	}
	rep(1,n<<1,i)if(!t[i].dfn)tarjan(i);
	rep(1,n,i)if(t[i].scc==t[i+n].scc){puts("IMPOSSIBLE");return 0;}puts("POSSIBLE");
	rep(1,n,i)printf("%d ",(t[i].scc>t[i+n].scc));return 0;
}

咕咕咕 (博主懒得一批，且深陷邪门码风的毒害，又老是幻想着搞博客 ~逃