题目描述
乃爱居住的国家有 (n) 座城市,这些城市与城市之间有 (n-1) 条公路相连接,并且保证这些城市两两之间直接或者间接相连。
我们定义两座城市之间的距离为这两座城市之间唯一简单路径上公路的总条数。
当乃爱位于第 (x) 座城市时,距离城市 (x) 距离不大于 (k) 的城市中的人都会认为乃爱天下第一可爱!
认为乃爱天下第一可爱的人们决定到乃爱所在的城市去拜访可爱的乃爱。我们定义这些城市的拥挤程度为:
- 距离城市(x)距离不大于(k)的城市中的人到达城市(x)时经过该城市的次数。
例如:
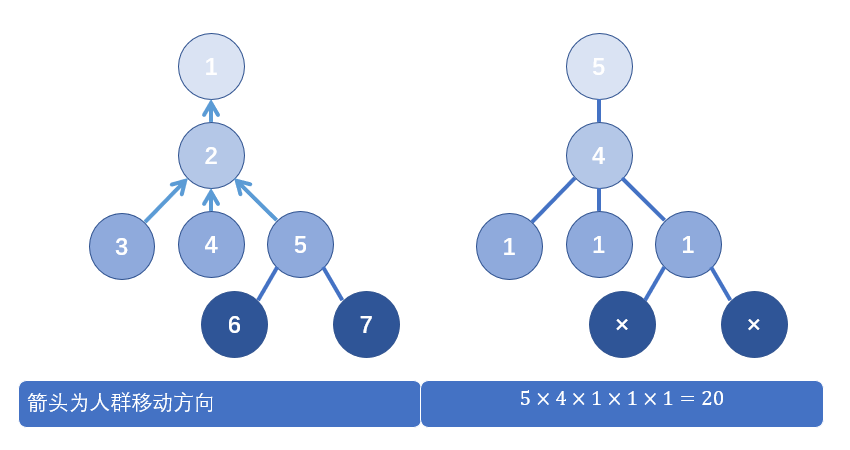
假设 (k=2) ,乃爱所在的城市是 (1) 号城市,树结构如上图所示时,受到影响的城市为 (1,2,3,4,5),因为五个城市距离 (1) 号城市的距离分别为:(0,1,2,2,2),所以这五个城市都会认为乃爱天下第一。
- (1)号城市到(1)号城市经过了(1)号城市。
- (2)号城市到(1)号城市经过了(1)号、(2)号城市。
- (3)号城市到(1)号城市经过了(1)号、(2)号、(3)号城市。
- (4)号城市到(1)号城市经过了(1)号、(2)号、(4)号城市。
- (5)号城市到(1)号城市经过了(1)号、(2)号、(5)号城市。
所以1号城市的拥挤程度是5,2号城市的拥挤程度是4,3号、4号、5号城市的拥挤程度都是1。
现在小w想要问你当乃爱依次位于第 1、2、3、4、5...n 座城市时,有多少座城市中的人会认为乃爱天下第一,以及受到影响城市的拥挤程度的乘积,由于这个数字会很大,所以要求你输出认为乃爱天下第一的城市拥挤程度乘积(mod 10^9+7) 后的结果。
输出描述:
输出两行。
第一行n个整数,表示当乃爱依次位于第 1、2、3、4、5. . .n 座城市时,有多少座城市中的人会认为乃爱天下第一。
第二行n个整数,表示当乃爱依次位于第 1、2、3、4、5. . .n 座城市时,受影响的城市拥挤程度乘积$ mod 10^9+7$ 后的结果。
80分暴力:(O(n^2)) 枚举一下顶点,随便搞搞就好了
贴点代码:(P2是处理链的情况)
namespace P1{
int ans1[N],ans2[N];
int dfs(int rt,int x,int f,int dis){
if(dis>K)return 0;int sz=1;
for(int i=0;i<edge[x].size();i++){
int y=edge[x][i];
if(y==f)continue;
sz=sz+dfs(rt,y,x,dis+1);
}
ans2[rt]=1ll*ans2[rt]*sz%P;
return sz;
}
void solve(){
for(int i=1;i<=n;i++)ans2[i]=1,ans1[i]=dfs(i,i,0,0);
for(int i=1;i<n;i++)printf("%d ",ans1[i]);
printf("%d
",ans1[n]);
for(int i=1;i<n;i++)printf("%d ",ans2[i]);
printf("%d
",ans2[n]);
exit(0);
}
}
int in[N];
namespace P2{
int id[N],ans1[N],ans2[N];
void pre_dfs(int x,int f,int cnt){
id[cnt]=x;
for(int i=0;i<edge[x].size();i++){
int y=edge[x][i];
if(y==f)continue;
pre_dfs(y,x,cnt+1);
}
}
int fac[N];
void solve(){
fac[0]=1;
for(int i=1;i<=K+10;i++)fac[i]=1ll*fac[i-1]*i%P;
int st;
for(int i=1;i<=n;i++)
if(in[i]==1){st=i;break;}
pre_dfs(st,0,1);
for(int i=1;i<=n;i++){
int l=min(K,i-1),r=min(K,n-i);
ans1[id[i]]=1+l+r;
ans2[id[i]]=1ll*ans1[id[i]]*fac[l]%P*fac[r]%P;
}
for(int i=1;i<n;i++)printf("%d ",ans1[i]);printf("%d
",ans1[n]);
for(int i=1;i<n;i++)printf("%d ",ans2[i]);printf("%d
",ans2[n]);
exit(0);
}
}
正解: DP + 换根
之前发过一篇比较简单的换根题的题解,只需要一些简单的分析,这道题要稍微复杂一些,要考虑比较多的东西。
先上代码:
#include<bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<endl
#define LL long long
using namespace std;
bool cur1;
const int N=100005,P=1e9+7;
int n,K;
vector<int>edge[N];
LL dp1[N][15],dp2[N][15];
LL kpow(LL x,LL y){
LL res=1;
while(y){
if(y&1)res=res*x%P;
x=x*x%P;
y>>=1;
}
return res;
}
LL inv(LL x){return kpow(x,P-2);}//不方便预处理(1e9+7),现场求逆元
void pre_dfs(int x,int f){
dp1[x][0]=1;
for(int i=0;i<=K;i++)dp2[x][i]=1;
for(int i=0;i<edge[x].size();i++){
int y=edge[x][i];
if(y==f)continue;
pre_dfs(y,x);
for(int j=1;j<=K;j++){
dp1[x][j]+=dp1[y][j-1]; //dp1[x][y]表示x子树里与x距离为y的城市个数
dp2[x][j]=dp2[x][j]*dp2[y][j-1]%P; //dp2[x][y]表示x子树里当K=y时拥挤度的乘积
}
}
LL sum=0;
for(int i=0;i<=K;i++){
sum+=dp1[x][i];
dp2[x][i]=dp2[x][i]*sum%P;//乘上dp[x][i]中x这个点的拥挤度
}
}
void cut_dp(int rt1,int rt2){//当前rt1为rt2的父节点,要切断rt1和rt2的联系
for(int i=1;i<=K;i++)dp2[rt1][i]=dp2[rt1][i]*inv(dp2[rt2][i-1])%P;//除掉rt2子树里的拥挤度乘积
LL sum=0;
for(int i=0;i<=K;i++){
sum+=dp1[rt1][i];
dp2[rt1][i]=dp2[rt1][i]*inv(sum)%P;
}sum=0;//把rt1这个点的拥挤程度除掉,因为后面换根后会dp1会发生变化
for(int i=0;i<=K;i++){
sum+=dp1[rt2][i];
dp2[rt2][i]=dp2[rt2][i]*inv(sum)%P;
}//把rt2的除掉
for(int i=1;i<=K;i++)dp1[rt1][i]-=dp1[rt2][i-1];//个数减掉
}
void link_dp(int rt1,int rt2){//当前rt1和rt2为没有关系的两个点,要连接rt1和rt2,使得rt1为rt2的父节点
for(int i=1;i<=K;i++)dp1[rt1][i]+=dp1[rt2][i-1];
LL sum=0;
for(int i=0;i<=K;i++){
sum+=dp1[rt1][i];
dp2[rt1][i]=dp2[rt1][i]*sum%P;
}sum=0;
for(int i=0;i<=K;i++){
sum+=dp1[rt2][i];
dp2[rt2][i]=dp2[rt2][i]*sum%P;
}
for(int i=1;i<=K;i++)dp2[rt1][i]=dp2[rt1][i]*dp2[rt2][i-1]%P;
}//同理cut_dp,顺序稍有改变
void change(int x,int y){// 当前x为y的父节点
cut_dp(x,y);// 切断x与y的联系
link_dp(y,x);// 将y作为父节点,x作为y的儿子,重新连接 y,x
}
LL ans1[N],ans2[N];
void dfs(int x,int f){
for(int i=0;i<=K;i++)ans1[x]+=dp1[x][i];
ans2[x]=dp2[x][K];//当前的dp1[x],dp2[x]都是以x为根时的结果,直接统计就是答案(统计方式的不同取决于定义的不同)
for(int i=0;i<edge[x].size();i++){
int y=edge[x][i];
if(y==f)continue;
change(x,y);//换根
dfs(y,x);
change(y,x);//换回来(还原现场)
}
}
bool cur2;
int main(){
// printf("%lf",(&cur2-&cur1)/1024.0/1024);
scanf("%d%d",&n,&K);
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
edge[u].push_back(v);
edge[v].push_back(u);
}
pre_dfs(1,0);
dfs(1,0);
for(int i=1;i<n;i++)printf("%lld ",ans1[i]);printf("%lld
",ans1[n]);
for(int i=1;i<n;i++)printf("%lld ",ans2[i]);printf("%lld
",ans2[n]);
return 0;
}
话说其实看看注释就差不多了。。
主要牵扯到一种很常用的换根套路: (cut) 和 (link)
普及一下英语单词。。 (link) : 连接
换根法:
先随便找一个点作为根节点使用,得到整个树每个节点的 (dp) 信息并且储存起来。(对应代码中的 (pre\_dfs))
考虑相邻节点换根,也就是假设根节点为 (x),然后整颗树的 (dp) 信息是以 (x) 为根的基础上进行构建的,(y) 节点为 (x) 节点的直接孩子。我们发现当整棵树的根节点由 (x) 转换为 (y) 时,改变的 (dp) 信息其实非常少,往往只影响到 (x,y) 两个节点。
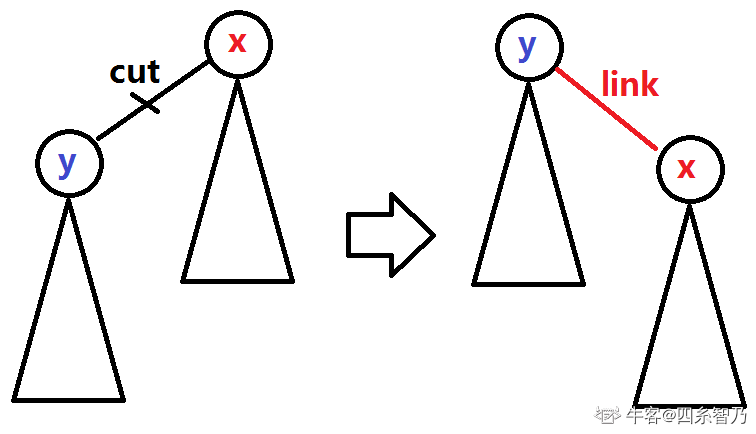
如图,当前 (x) 为 (y) 的父亲,我们已经处理好了 (x) 的答案,现在要换根,将 (y) 转化为根。
考虑把换根操作分成两部执行:
-
切断 (x) 与 (y) 的联系((cut))
-
重连 (x) 与 (y),使 (y) 是 (x) 的父亲 ( (link) )
于是就有了一个换根问题的大体方法。
具体细节可以见代码注释。