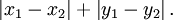POJ2926 Requirements(最远曼哈顿距离)

题目链接。

分析：

借机学习了一下曼哈顿距离问题。

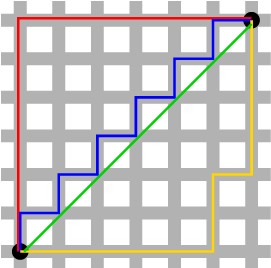（这图很好）

我们可以定义曼哈顿距离的正式意义为L₁-距离或城市区块距离，也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。

例如在平面上，座标（x₁, y₁）的点P₁与座标（x₂, y₂）的点P₂的曼哈顿距离为：

以二维平面为例：

设距离最远的两点为 i, j，可知所求的最大距离必定有以下四种形式之一：

(xi-xj)+(yi-yj), (xj-xi)+(yi-yj), (xi-xj)+(yj-yi), (xj-xi)+(yj-yi) 变形一下，把相同点的坐标放到一起，

即 (xi+yi)-(xj+yj), (-xi+yi)-(-xj+yj), (xi-yi)-(xj-yj), (-xi-yi)-(-xj-yj)，可以发现即去绝对值之后把同一点的坐标放在一起，对应坐标符号相同。

假如我们用 0 表示负号，用 1 表示正号，那么 (xi+yi) 可以表示为 11。

那么要表示一个维数为 dem 的所有状态，只需要用 0 ~ (2^dem-1) 的所有二进制就可以了。

于是只要对所有的点 (xi,yi)，依次计算出 (xi+yi), (xi-yi), (-xi+yi), (-xi-yi)这四种形式，然后把每个点i算出来的这四种情况的最大值、最小值分别记录（更新）到数组 max[] 和 min[] 中，然后枚举每一种去绝对值的组合，组合后的最大值即为 answer。

详情请看代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <stack>

using namespace std;

const int maxn = 100000+10;
const int dem = 5;  //维数
const double INF = (1e200);

struct Point{
    double x[dem];
}p[maxn];

int n;
double minx[1<<dem], maxx[1<<dem];

double solve() {
    int tmp = 1<<dem;

    for(int i=0; i<tmp; i++) {
        minx[i] = INF;
        maxx[i] = -INF;
    }

    for(int i=0; i<n; i++) {
        for(int j=0; j<tmp; j++) {
            int t = j;
            double s = 0;
            for(int k=0; k<dem; k++) {
                if(t & 1) s += p[i].x[k];
                else s -= p[i].x[k];
                t >>= 1;
            }
            if(maxx[j] < s) maxx[j] = s;
            if(minx[j] > s) minx[j] = s;
        }
    }

    double ans = -INF;
    for(int i=0; i<tmp; i++) {
        if(maxx[i] - minx[i] > ans)
            ans = maxx[i] - minx[i];
    }

    return ans;
}

int main(){

    while(scanf("%d", &n) != EOF) {
        for(int i=0; i<n; i++) {
            for(int j=0; j<dem; j++) {
                scanf("%lf", &p[i].x[j]);
            }
        }
        printf("%.2f\n", solve());
    }

    return 0;
}

维基百科：http://zh.wikipedia.org/wiki/%E6%9B%BC%E5%93%88%E9%A0%93%E8%B7%9D%E9%9B%A2

代码参考：http://blog.csdn.net/taozifish/article/details/7574294

讲解参考：http://www.cnblogs.com/lmnx/articles/2479747.html