第二章 信息的表示和处理
2.1 信息存储
2.1.1 十六进制
2.1.2 字数据大小
2.1.3 寻址和字节顺序
1.地址:对象所使用的字节中最小的地址
2.大端法:最高有效字节在前
小端法:最低有效字节在前(大多Intel兼容机使用)
3.发送方机器(内部代码)——>网络应用程序(网络标准)——>接收方机器(内部代码)
4.小程序——打印程序对象的字节表示
1 #include <stdio.h>
2 using namespace std;
3
4 typedef unsigned char * byte_pointer;//定义类型:指向unsigned char的指针
5
6 void show_byte(byte_pointer start, size_t len){
7 size_t i;
8 for(i = 0; i < len; ++i)
9 printf(" %.2x", start[i]);//%.2x表示整数必须用至少两个数字的十六进制格式输出
10 printf("
");
11 }
12
13 void show_int(int x){
14 show_byte((byte_pointer) &x, sizeof(int));
15 }
16
17 void show_float(float x){
18 show_byte((byte_pointer) &x, sizeof(float));
19 }
20
21 void show_double(double x){
22 show_byte((byte_pointer) &x, sizeof(double));
23 }
24
25 void show_pointer(void * x){//void*是特殊类型的指针,没有相关联的类型信息
26 show_byte((byte_pointer) &x, sizeof(void *));
27 }
28
29 int main(){
30 int x;
31 float y;
32 double z;
33 while(scanf("%d %f %lf", &x, &y, &z)){
34 show_int(x);
35 show_float(y);
36 show_double(z);
37 show_pointer(&x);
38 show_pointer(&y);
39 show_pointer(&z);
40 }
41 return 0;
42 }
输入
1
1
1
-1
-1.0
-1.0
12345
1.001
1.001
输出
01 00 00 00
00 00 80 3f
00 00 00 00 00 00 f0 3f
98 f5 bf ef fe 7f 00 00
94 f5 bf ef fe 7f 00 00
88 f5 bf ef fe 7f 00 00
ff ff ff ff
00 00 80 bf
00 00 00 00 00 00 f0 bf
98 f5 bf ef fe 7f 00 00
94 f5 bf ef fe 7f 00 00
88 f5 bf ef fe 7f 00 00
39 30 00 00
c5 20 80 3f
6a bc 74 93 18 04 f0 3f
98 f5 bf ef fe 7f 00 00
94 f5 bf ef fe 7f 00 00
88 f5 bf ef fe 7f 00 00
我的电脑是MaxOS,可以看出它是64位系统,采用小端法表示
5.可以通过在终端(mac是terminal,windows是命令行工具)执行命令man ascii得到一张ASCII字符码表,回车后运行结果如下
ASCII(7) BSD Miscellaneous Information Manual ASCII(7)
NAME
ascii -- octal, hexadecimal and decimal ASCII character sets
DESCRIPTION
The octal set:
000 nul 001 soh 002 stx 003 etx 004 eot 005 enq 006 ack 007 bel
010 bs 011 ht 012 nl 013 vt 014 np 015 cr 016 so 017 si
020 dle 021 dc1 022 dc2 023 dc3 024 dc4 025 nak 026 syn 027 etb
030 can 031 em 032 sub 033 esc 034 fs 035 gs 036 rs 037 us
040 sp 041 ! 042 " 043 # 044 $ 045 % 046 & 047 '
050 ( 051 ) 052 * 053 + 054 , 055 - 056 . 057 /
060 0 061 1 062 2 063 3 064 4 065 5 066 6 067 7
070 8 071 9 072 : 073 ; 074 < 075 = 076 > 077 ?
100 @ 101 A 102 B 103 C 104 D 105 E 106 F 107 G
110 H 111 I 112 J 113 K 114 L 115 M 116 N 117 O
120 P 121 Q 122 R 123 S 124 T 125 U 126 V 127 W
130 X 131 Y 132 Z 133 [ 134 135 ] 136 ^ 137 _
140 ` 141 a 142 b 143 c 144 d 145 e 146 f 147 g
150 h 151 i 152 j 153 k 154 l 155 m 156 n 157 o
160 p 161 q 162 r 163 s 164 t 165 u 166 v 167 w
170 x 171 y 172 z 173 { 174 | 175 } 176 ~ 177 del
The hexadecimal set:
00 nul 01 soh 02 stx 03 etx 04 eot 05 enq 06 ack 07 bel
08 bs 09 ht 0a nl 0b vt 0c np 0d cr 0e so 0f si
10 dle 11 dc1 12 dc2 13 dc3 14 dc4 15 nak 16 syn 17 etb
18 can 19 em 1a sub 1b esc 1c fs 1d gs 1e rs 1f us
20 sp 21 ! 22 " 23 # 24 $ 25 % 26 & 27 '
28 ( 29 ) 2a * 2b + 2c , 2d - 2e . 2f /
30 0 31 1 32 2 33 3 34 4 35 5 36 6 37 7
38 8 39 9 3a : 3b ; 3c < 3d = 3e > 3f ?
40 @ 41 A 42 B 43 C 44 D 45 E 46 F 47 G
48 H 49 I 4a J 4b K 4c L 4d M 4e N 4f O
50 P 51 Q 52 R 53 S 54 T 55 U 56 V 57 W
58 X 59 Y 5a Z 5b [ 5c 5d ] 5e ^ 5f _
60 ` 61 a 62 b 63 c 64 d 65 e 66 f 67 g
68 h 69 i 6a j 6b k 6c l 6d m 6e n 6f o
70 p 71 q 72 r 73 s 74 t 75 u 76 v 77 w
78 x 79 y 7a z 7b { 7c | 7d } 7e ~ 7f del
The decimal set:
0 nul 1 soh 2 stx 3 etx 4 eot 5 enq 6 ack 7 bel
8 bs 9 ht 10 nl 11 vt 12 np 13 cr 14 so 15 si
16 dle 17 dc1 18 dc2 19 dc3 20 dc4 21 nak 22 syn 23 etb
24 can 25 em 26 sub 27 esc 28 fs 29 gs 30 rs 31 us
32 sp 33 ! 34 " 35 # 36 $ 37 % 38 & 39 '
40 ( 41 ) 42 * 43 + 44 , 45 - 46 . 47 /
48 0 49 1 50 2 51 3 52 4 53 5 54 6 55 7
56 8 57 9 58 : 59 ; 60 < 61 = 62 > 63 ?
64 @ 65 A 66 B 67 C 68 D 69 E 70 F 71 G
72 H 73 I 74 J 75 K 76 L 77 M 78 N 79 O
80 P 81 Q 82 R 83 S 84 T 85 U 86 V 87 W
88 X 89 Y 90 Z 91 [ 92 93 ] 94 ^ 95 _
96 ` 97 a 98 b 99 c 100 d 101 e 102 f 103 g
104 h 105 i 106 j 107 k 108 l 109 m 110 n 111 o
112 p 113 q 114 r 115 s 116 t 117 u 118 v 119 w
120 x 121 y 122 z 123 { 124 | 125 } 126 ~ 127 del
FILES
/usr/share/misc/ascii
HISTORY
An ascii manual page appeared in Version 7 AT&T UNIX.
BSD June 5, 1993 BSD
(END)
2.1.4 表示字符串
1.十进制数字‘y’的ascii码正好是0x3y
2.strlen(str)函数不计算终止的空字符(ascii码为0x00)
3.字符编码方式:
(1)ASCII (American Standard Code for Information interchange)
(2)Unicode (Unique Code)
(3)UTF-8 / UTF-16 / UFT-32 (Unicode Transformation Format)
详见文章:https://knightyun.github.io/2019/01/27/ascii-unicode
2.1.5 表示代码
2.1.6 布尔代数(Boolean Algebra)简介
1.布尔运算&对|有分配律:a&(b|c) = (a&b)|(a&c)
布尔运算|对&有分配律:a|(b&c) = (a|b)&(a|c)
2.位向量:长度为w,由0和1组成的串
应用:表示有限集合/压位运算(例:[01101010]表示集合{1,3,5,6}),位向量掩码/屏蔽信号
3.布尔环(Boolean ring),类似于整环/整数环
“加法”逆元:^类似于+; 每个整数x有加法逆元-x使得x+(-x)=0,类似地,每个布尔元素a都有“加法逆元”a使得a^a=0; 有趣的性质:(a^b)^a=b
1 //这是一个不需要第三个量的交换函数,不过它并没有性能上的优势
2 void inplace_swap(int *x, int *y){//*x = a, *y = b
3 *x = *x ^ *y;//*x = a^b, *y = b
4 *y = *x ^ *y;//*x = a^b, *y = a
5 *x = *x ^ *y;//*x = b, *y = a
6 }
2.1.7 C语言中的位级运算:&, |, ^, ~
2.1.8 C语言中的逻辑运算: &&, ||, !
2.1.9 C语言中的移位运算:>>, <<
1.逻辑右移(高位补0,无符号数进行逻辑右移)
算数右移(高位补符号位,有符号数进行算数右移)
2.运算符优先级:见https://blog.csdn.net/changexhao/article/details/82556761
(1)初级运算符[]().->
(2)单目运算符
(3)算数运算符
(4)移位运算符
(5)关系运算符
(6)位级运算符
(7)逻辑运算符
(8)赋值运算符
2.2 整数表示
2.2.1 整形数据类型
2.2.2 无符号数的编码(unsigned)
2.2.3 补码编码(two's-complement)
1.<limits.h>库:INT_MIN, INT_MAX, UINT_MAX
<stdint.h>库:intN_t, UintN_t (t = 16,32,64等)
(我在xcode上没有include这两个库也能直接使用INT_MIN、int32_t等)
2.有符号数的表示方法
(1)补码(two's-complement):最高位权重为-2^(w-1)
(2)反码(ones' complement):最高位权重为-(2^(w-1)-1)
(3)原码(sign-magnitude):最高位为1表示所有其他位权重为负
注:(2)(3)中0的表示法不唯一,有+0和-0两种
2.2.4 有符号数和无符号数之间的转换
(可能)改变数值,但不改变位表示
1.补码转换为无符号数(w位):
TMin <= x < 0, T2U(x) = x + 2^w
0 <= x <= TMax, T2U(x) = x
2.无符号数转换为有符号数(w位):
0 <= x <= TMax, U2T(x) = x
TMax < x <= UMax, U2T(x) = x - 2^w
2.2.5 C语言中的有符号数和无符号数
1.数字常量默认为有符号数,加上后缀u或U可创建无符号数常量
2.类型转换的方式:
(1)显式:强制类型转换
(2)隐式:不同类型变量间赋值
3.%d有符号十进制,%u无符号十进制,%o八进制,%x十六进制
4.C语言对于同时包含有符号数和无符号数的表达式,会隐式地将有符号数转换为非负的无符号数
1 /*
2 这是一个测试函数
3 注:TMin写成-2147483647-1而非-2147483648
4 是因为limits.h中定义INT_MIN=-INT_MAX-1,以规避某些奇怪的现象
5 */
6 #include <cstdio>
7 using namespace std;
8
9 int main(){
10 printf("-1 < 0u = %d
", -1 < 0u);
11 printf(" -1 = 0x%x
", -1);
12 printf(" 0u = 0x%x
", 0u);
13
14 printf("2147483547 > (int)2147483648u = %d
", 2147483547 > (int)2147483648u);
15 printf(" 2147483547 = 0x%x
", 2147483547);
16 printf(" (int)2147483648u = 0x%x
", (int)2147483648u);
17
18 printf("-2147483647-1u < 2147483647 = %d
", -2147483647-1u < 2147483647);
19 printf(" -2147483647-1u = 0x%x
", -2147483647-1u);
20 printf(" 2147483647 = 0x%x
", 2147483647);
21
22 printf("-2147483647-1u < -2147483647 = %d
", -2147483647-1u < -2147483647);
23 printf(" -2147483647-1u = 0x%x
", -2147483647-1u);
24 printf(" -2147483647 = 0x%x
", -2147483647);
25 return 0;
26 }
运行结果如下
-1 < 0u = 0
-1 = 0xffffffff
0u = 0x0
2147483547 > (int)2147483648u = 1
2147483547 = 0x7fffff9b
(int)2147483648u = 0x80000000
-2147483647-1u < 2147483647 = 0
-2147483647-1u = 0x80000000
2147483647 = 0x7fffffff
-2147483647-1u < -2147483647 = 1
-2147483647-1u = 0x80000000
-2147483647 = 0x80000001
2.4 浮点数
2.4.1 二进制小数
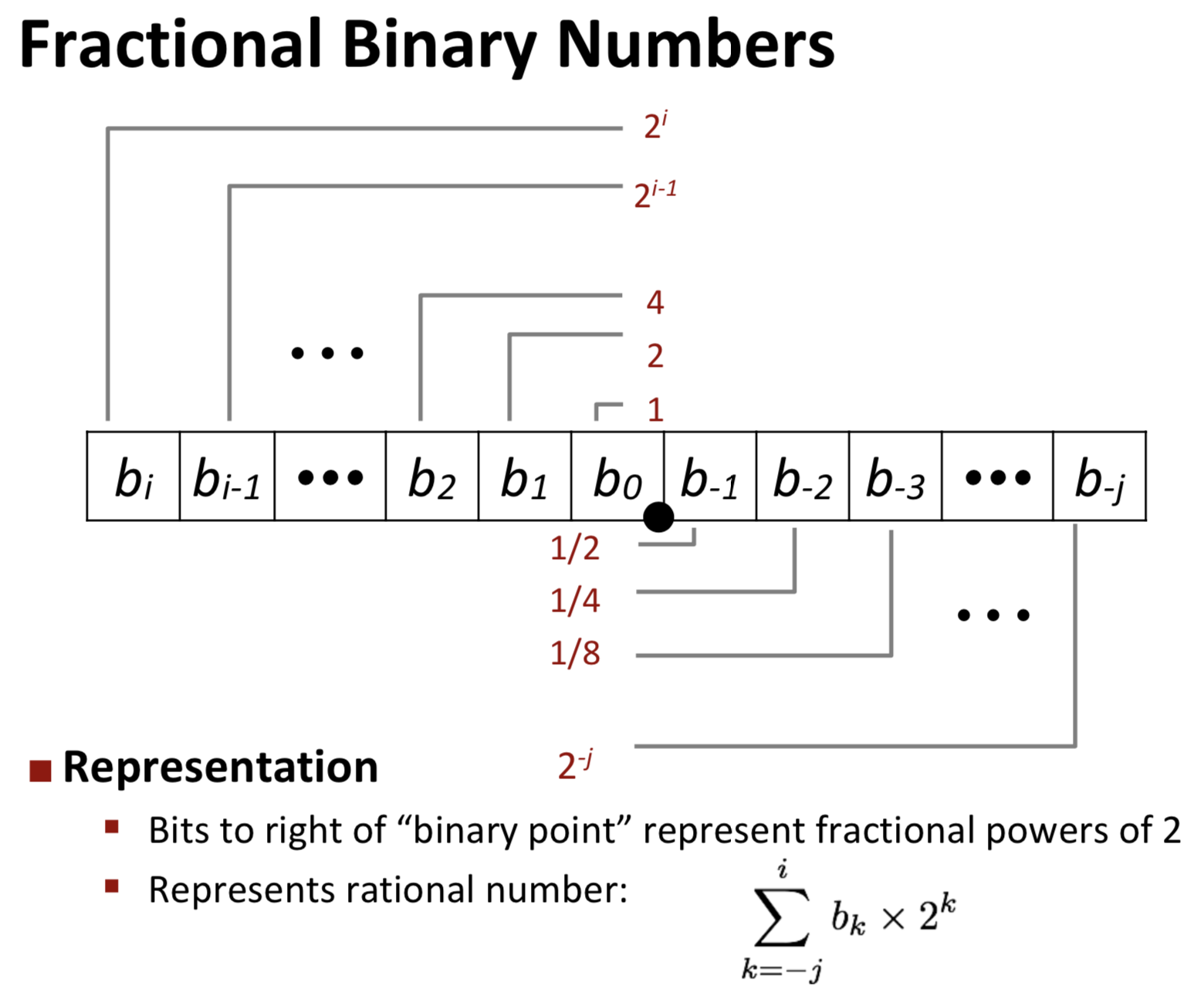
2.4.2 IEEE浮点表示
1.表示形式:![]()
(1)符号(sign)s: 表示+-
(2)尾数(significand)M:二进制小数,取值范围为[1,2)或[0,1)
(3)阶码(exponent)E:对浮点数加权,权重为2的E次幂
2.编码:![]()
s编码符号sign s,exp编码阶码exponent E,frac编码尾数significand M

3.三种情况
(1)规格化的(noemalized): exp!=00...0 && exp!=11...1
i. 阶码 E = exp - bias, bias = 2^(k-1)-1, k=exp的位数
ii. 尾数 M = 1.xx...x = 1.frac的位(隐含的以1开头的表示)
(2)非规格化的(denormalized): exp == 00...0
i. 阶码 E = 1 - bias, bias = 2^(k-1)-1, k=exp的位数
ii. 尾数 M = 0.xx...x = 0.frac的位
iii.注意:0.0有两种表示方法+0.0和-0.0,符号位分别为0或1,其他位全部为0
(3)特殊值: exp == 11...1
i. 无穷:frac = 00...0, s=0或1表示+∞或-∞,能够表示溢出的运算结果,如x/0
ii. Nan(not a number): frac != 00...0, 表示非实数的运算结果,如根号-1,∞-∞
4.三种情况的数字分布

非规格化数字的阶码定义为E=1-bias可以补偿非规格化的尾数没有隐含的开头1,有助于数字表示的平滑转变;否则,在绝对值最大的非规格化数字(其二进制表示为0 00...0 11...1)和绝对值最小的规格化数字(其二进制表示为0 00...01 00...0)之间将存在跳跃
2.4.3 数字示例
1. 处理正浮点数时,若按照无符号整数解释他们的二进制表示,则可以发现它们的大小顺序不变;负浮点数只需要倒序