数据结构与算法——编程作业——第三章 栈与队列

1:中缀表达式的值

总时间限制: 

200ms

 

内存限制: 

1024kB

描述

人们熟悉的四则运算表达式称为中缀表达式，例如(23+34*45/(5+6+7))。在程序设计语言中，可以利用堆栈的方法把中缀表达式转换成保值的后缀表达式（又称逆波兰表示法），并最终变为计算机可以直接执行的指令，得到表达式的值。

给定一个中缀表达式，编写程序，利用堆栈的方法，计算表达式的值。

输入

第一行为测试数据的组数N
接下来的N行，每行是一个中缀表达式。表达式中只含数字、四则运算符和圆括号，操作数都是正整数，数和运算符、括号之间没有空格。中缀表达式的字符串长度不超过600。

输出

对每一组测试数据输出一行，为表达式的值

样例输入

3
3+5*8
(3+5)*8
(23+34*45/(5+6+7))

样例输出

43
64
108

提示

注意：运算过程均为整数运算（除法运算'/'即按照C++定义的int除以int的结果，测试数据不会出现除数为0的情况），输出结果也为整数（可能为负）。
中间计算结果可能为负。

这题有点儿变态qaq

解题思路是：中缀表达式-->后缀表达式-->计算后缀表达式

step 1: 中缀表达式-->后缀表达式

中缀表达式a + b*c + (d * e + f) * g，其转换成后缀表达式则为a b c * + d e * f  + g * +。

转换过程需要用到栈，具体过程如下：

1）如果遇到操作数，我们就直接将其输出。

2）如果遇到操作符，则我们将其放入到栈中，遇到左括号时我们也将其放入栈中。

3）如果遇到一个右括号，则将栈元素弹出，将弹出的操作符输出直到遇到左括号为止。注意，左括号只弹出并不输出。

4）如果遇到任何其他的操作符，如（“+”， “*”，“（”）等，从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后，才将遇到的操作符压入到栈中。有一点需要注意，只有在遇到" ) "的情况下我们才弹出" ( "，其他情况我们都不会弹出" ( "。

5）如果我们读到了输入的末尾，则将栈中所有元素依次弹出。

step 2:计算后缀表达式

后缀表达式的求值过程为，从左到右扫描后缀表达式：

1）如果遇到操作数，将其压入栈中。

2）如果遇到操作符，则从栈中弹出两个操作数，计算结果，然后把结果入栈。

3）直到遍历完后缀表达式，则计算完成，此时的栈顶元素即为计算结果。

我的代码思路

我在做的时候为了简化代码，直接两大步骤并为一大步骤了，实现思路不变。

具体来说，我用了一个数字栈和一个符号栈来分别储存操作数和操作符；在遇到step1中(3)(4)(5)的“输出/弹出操作符”的情况时，实施类似step2中(2)的做法：从数字栈中弹出两个操作数，从符号栈中弹出一个操作符，计算这三者的运算结果，把结果放回数字栈中；最终，符号栈应该为空，数字栈应该只剩下一个元素，也就是表达式的值，其余情况均为错误输入。

我的代码

#include <cstdio>
#include <stack>
#include <cstring>
using namespace std;

//判断运算符号优先级是否满足c1>=c2
bool prior(const char c1, const char c2){
    if((c1=='-'||c1=='+') && (c2=='*'||c2=='/'))
        return false;
    else
        return true;
}

//函数Op2Num(): 操作两个数字的运算;
void Op2Num(stack<int> & num, stack<char> & op){
    int num1, num2;//取数字栈顶的两个操作数
    num1 = num.top(); num.pop();
    num2 = num.top(); num.pop();
    switch(op.top()){//操作数字栈顶两数字并重新入栈
        case '+': num.push(num2+num1); break;
        case '-': num.push(num2-num1); break;
        case '*': num.push(num2*num1); break;
        case '/': num.push(num2/num1); break;
        default: printf("       something wrong in Op2Num
");
    }
    op.pop();//弹出符号栈顶符号
}

//函数OpeNum():
//cur传入字符')','+','-','*','/',表明调用本函数的触发条件
void OpeNum(stack<int> & num, stack<char> & op, char cur){
    while(!op.empty() && op.top()!='(' && prior(op.top(), cur))
        Op2Num(num, op);
    switch(cur){
        case ')':
            if(op.top() == '(')
                op.pop();//弹左括号
            break;
        default:
            op.push(cur);//当前符号入符号栈
    }
    return;
}

//从字符串中取数字
int GetNum(char * str, int & i){
    int temp = 0;
    while(str[i]>='0' && str[i]<='9'){
        temp = temp*10 + str[i] - '0';
        ++i;
    }
    --i;
    return temp;
}

//表达式结束，所有符号弹栈
void PopAll(stack<int> & num, stack<char> & op){
    while(!op.empty())
        Op2Num(num, op);
    return;
}

//中缀表达式运算
int CalNifix(char * str){
    stack<int> num;//数字栈
    stack<char> op;//符号栈
    for(int i=0; str[i]; ++i){
        switch(str[i]){
            case '(':
                op.push('('); break;//左括号入栈
            case ')':
            case '+':
            case '-':
            case '*':
            case '/':
                OpeNum(num, op, str[i]); break;//操作运算
            default:
                num.push(GetNum(str, i));//取数字入数字栈
        }
    }
    PopAll(num, op);//表达式结束，所有符号弹栈
    return num.top();//返回运算结果
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--){
        char str[650];//储存中缀表达式
        scanf("%s", str);
        printf("%d
", CalNifix(str));
    }
    return 0;
}

我的代码是按照自己的思路写的，大家当然可以把step1和step2分开做、依次做，我想可能会更容易理解，结构也更清晰。

但是无论如何，请一定一定不要直接copy，一定一定要自己看懂思路后，独立写一遍，这样才能学到东西嘛！加油！

2:滑动窗口

总时间限制: 

12000ms

 

内存限制: 

65536kB

描述

给定一个长度为n（n<=10^6）的数组。有一个大小为k的滑动窗口从数组的最左端移动到最右端。你可以看到窗口中的k个数字。窗口每次向右滑动一个数字的距离。

下面是一个例子：

数组是 [1 3 -1 -3 5 3 6 7]， k = 3。

窗口位置	最小值	最大值
[1  3  -1] -3  5  3  6  7	-1	3
1 [3  -1  -3] 5  3  6  7	-3	3
1  3 [-1  -3  5] 3  6  7	-3	5
1  3  -1 [-3  5  3] 6  7	-3	5
1  3  -1  -3 [5  3  6] 7	3	6
1  3  -1  -3  5 [3  6  7]	3	7

你的任务是得到滑动窗口在每个位置时的最大值和最小值。

输入

输入包括两行。
第一行包括n和k，分别表示数组的长度和窗口的大小。
第二行包括n个数字。

输出

输出包括两行。
第一行包括窗口从左至右移动的每个位置的最小值。
第二行包括窗口从左至右移动的每个位置的最大值。

样例输入

8 3
1 3 -1 -3 5 3 6 7

样例输出

-1 -3 -3 -3 3 3
3 3 5 5 6 7

曲折历程

啊，这是一道看似简单的题目，做了好久才AC。

第一想法是暴力查找，代码简单然鹅TLE了，哇地一声哭出来（不是

为了让这个暴力代码更简洁，我甚至还学了min_element()和max_element()函数；这两个函数当然是很有用的，可是我用错了位置，不过还是打算记录一下

/*这是一段伪代码，用于指示函数用法*/

#include <algorithm>

std::min_element
    default (1)	
        template <class ForwardIterator>
        ForwardIterator min_element (ForwardIterator first, ForwardIterator last);
    custom (2)	
        template <class ForwardIterator, class Compare>
        ForwardIterator min_element (ForwardIterator first, ForwardIterator last,Compare comp);

std::max_element
    default (1)	
    template <class ForwardIterator>
        ForwardIterator max_element (ForwardIterator first, ForwardIterator last);
    custom (2)
    template <class ForwardIterator, class Compare>
        ForwardIterator max_element (ForwardIterator first, ForwardIterator last,Compare comp);

 程序如下

#include <cstdio>
#include <algorithm>
using namespace std;

int main(){
    int n, k;
    int t[1000010];
    scanf("%d %d", &n, &k);
    for(int i=0; i<n; ++i)
        scanf("%d", t+i);
    for(int i=k; i<=n; ++i)
        printf("%d ",* min_element(t+i-k, t+i));
    printf("
");
    for(int i=k; i<=n; ++i)
        printf("%d ",* max_element(t+i-k, t+i));
    printf("
");
    return 0;
}

。。。

 我天真地以为把min_element()和max_element()函数换成for循环就会省时间，毕竟类比一下：用memset()给数组清零比for循环清零要慢许多，于是产生了下面的程序

#include <cstdio>
#include <algorithm>
using namespace std;

int main(){
    int n, k, t_min, t_max;
    int t[1000010], m[1000010];
    scanf("%d %d", &n, &k);
    for(int i=0; i<n; ++i)
        scanf("%d", t+i);
    for(int i=k; i<=n; ++i){
        t_min = t_max = t[i-k];
        for(int j=i-k+1; j<i; ++j){
            t_min = min(t_min, t[j]);
            t_max = max(t_max, t[j]);
        }
        m[i] = t_max;
        printf("%d ", t_min);
    }
    printf("
");
    for(int i=k; i<=n; ++i)
        printf("%d ", m[i]);
    printf("
");
    return 0;
}

不出预料地再次TLE

正经答案

最终我向度娘屈服了，查了一下，原来大家都是用单调队列实现解决滑动窗口问题的，贴几个讲得比较详细的帖子链接，因为我懒hh

1.https://www.acwing.com/solution/acwing/content/2499/

2.https://www.cnblogs.com/llke/p/10780121.html

我自己写的代码如下：

#include <iostream>
using namespace std;

#define N 1000010

//输出滑动窗口最小值
void PrintMin(int * num, const int n, const int k){
    //p_min[head...tail]储存当前窗口内的单调序列
    int p_min[n], head=0, tail=-1;
    for(int i=0; i<n; ++i){
        while(head<=tail && num[i]<=num[p_min[tail]])
            --tail;//队尾大元素元素出队
        p_min[++tail] = i;//元素i入队尾
        while(p_min[head]<=i-k)
            ++head;//队头窗口外元素出队
        if(i>=k-1)//输出当前窗口最小值
            cout << num[p_min[head]] << ' ';
    }
    cout << endl;
}

//输出滑动窗口最大值
void PrintMax(int * num, const int n, const int k){
    int p_max[n], head=0, tail=-1;
    for(int i=0; i<n; ++i){
        while(head<=tail && num[i]>=num[p_max[tail]])
            --tail;
        p_max[++tail] = i;
        while(p_max[head]<=i-k)
            ++head;
        if(i>=k-1)
            cout << num[p_max[head]] << ' ';
    }
    cout << endl;
}

int main() {
    int n, k, num[N];
    cin >> n >> k;
    for(int i=0; i<n; ++i)
        cin >> num[i];
    PrintMin(num, n, k);
    PrintMax(num, n, k);
    return 0;
}

观察发现，PrintMin()和PrintMax()函数的重复之处过多，唯一的差别在于“--tail”的时候是“队尾大元素出队”还是“队尾小元素出队”。很自然地想到，我们可以利用函数指针传递一个比较函数，以简化程序、合二为一。代码如下：

#include <iostream>
using namespace std;

#define N 1000010

bool MyMin(int a, int b){return a<=b;}
bool MyMax(int a, int b){return a>=b;}

void Print(int * num, const int n, const int k, bool (*f)(int,int)){
    //p[head...tail]储存当前窗口内的单调序列
    int p[n], head=0, tail=-1;
    for(int i=0; i<n; ++i){
        while(head<=tail && f(num[i],num[p[tail]]))
            --tail;//队尾元素出队
        p[++tail] = i;//元素i入队尾
        while(p[head]<=i-k)
            ++head;//队头窗口外元素出队
        if(i>=k-1)//输出当前窗口最值
            cout << num[p[head]] << ' ';
    }
    cout << endl;
}

int main() {
    int n, k, num[N];
    cin >> n >> k;
    for(int i=0; i<n; ++i)
        cin >> num[i];
    Print(num, n, k, MyMin);
    Print(num, n, k, MyMax);
    return 0;
}

后来又想到，可以通过把cin-cout换成scanf-printf，以及在函数前加上inline字样来减少运行用时，代码如下：

#include <stdio.h>
using namespace std;

#define N 1000010

bool MyMin(int a, int b){return a<=b;}
bool MyMax(int a, int b){return a>=b;}

inline void Print(int * num, const int n, const int k, bool (*f)(int,int)){
    //p[head...tail]储存当前窗口内的单调序列
    int p[n], head=0, tail=-1;
    for(int i=0; i<n; ++i){
        while(head<=tail && f(num[i],num[p[tail]]))
            --tail;//队尾元素出队
        p[++tail] = i;//元素i入队尾
        while(p[head]<=i-k)
            ++head;//队头窗口外元素出队
        if(i>=k-1)//输出当前窗口最值
            printf("%d ", num[p[head]]);
    }
    printf("
");
}

int main() {
    int n, k, num[N];
    scanf("%d %d", &n, &k);
    for(int i=0; i<n; ++i)
        scanf("%d", num+i);
    Print(num, n, k, MyMin);
    Print(num, n, k, MyMax);
    return 0;
}

滑动窗口1.0、2.0、3.0（从上到下）的OJ运行测试结果如下：

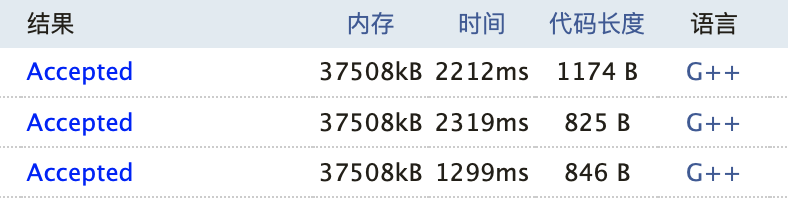
 可以看到它们在运行效率上有了一些提升，而且我还学到了不少新东西，虽然花了很多时间，但还是好开星！！！

 

3:栈的基本操作

总时间限制: 

1000ms

 

内存限制: 

1000kB

描述

栈是一种重要的数据结构，它具有push k和pop操作。push k是将数字k加入到栈中，pop则是从栈中取一个数出来。

栈是后进先出的：把栈也看成横向的一个通道，则push k是将k放到栈的最右边，而pop也是从栈的最右边取出一个数。

假设栈当前从左至右含有1和2两个数，则执行push 5和pop操作示例图如下：

          push 5          pop

栈   1 2  ------->  1 2 5 ------>  1 2

现在，假设栈是空的。给定一系列push k和pop操作之后，输出栈中存储的数字。若栈已经空了，仍然接收到pop操作，

则输出error。

输入

第一行为m，表示有m组测试输入，m<100。
每组第一行为n，表示下列有n行push k或pop操作。（n<150）
接下来n行，每行是push k或者pop，其中k是一个整数。
（输入保证同时在栈中的数不会超过100个）

输出

对每组测试数据输出一行。该行内容在正常情况下，是栈中从左到右存储的数字，数字直接以一个空格分隔，如果栈空，则不作输出；但若操作过程中出现栈已空仍然收到pop，则输出error。

样例输入

2
4
push 1
push 3
pop
push 5
1
pop

样例输出

1 5
error

我的答案

#include <stdio.h>
#include <stack>
using namespace std;

//函数：操作栈
void OpStack(){
    stack<int> st;
    int n, t;
    char cmd[5];
    bool flag=1;
    scanf("%d", &n);
    while(n--){
        scanf("%s", cmd);
        if(cmd[1] == 'u'){//push
            scanf("%d", &t);
            st.push(t);
        }
        else{//pop
            if(!st.empty())
                st.pop();
            else//error
                flag = 0;
        }
    }
    if(flag){//从栈底向栈顶输出，要倒一下
        stack<int> _st;
        while(!st.empty()){
            _st.push(st.top());
            st.pop();
        }
        while(!_st.empty()){
            printf("%d ", _st.top());
            _st.pop();
        }
    }
    else
        printf("error");
    printf("
");
    return;
}

int main() {
    int m;
    scanf("%d",&m);
    while(m--)
        OpStack();
    return 0;
}

这题比较简单～

我去写lab了，一起加油w