算法1---随机生成算法

本文主的主要内容是一些随机算法，主要有四种，下面来详细的介绍：

1 生成随机数

一般c语言中提供了随机数生成函数，

其一是伪随机数--rand：用于返回一个0-32767之间的伪随机数；

其二是随机种子函数--srand：用来初始化随机数发生器的随机种子

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main()
{
    int i,j;
    srand((int)time(0));
    for (int i = 0; i < 10; i++)
    {
        for (int j = 0; j < 10; j++)
        {
            printf("%d  ",rand());
        }
        printf("
");
    }
    return 0;
}

当然也可以生成一定范围内的随机数

比如生成0——100之间的随机数

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main()
{
    int i,j;
    srand((int)time(0));
    for (int i = 0; i < 10; i++)
    {
        for (int j = 0; j < 10; j++)
        {
            printf("%d  ",rand()*100/32767);
        }
        printf("
");
    }
    return 0;
}

也可以生成100——200之间的随机数

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main()
{
    int i,j;
    srand((int)time(0));
    for (int i = 0; i < 10; i++)
    {
        for (int j = 0; j < 10; j++)
        {
            printf("%d  ",rand()/1000+100);
        }
        printf("
");
    }
    return 0;
}

2 生成[0,1]之间均匀分布的随机数算法

 

 

 

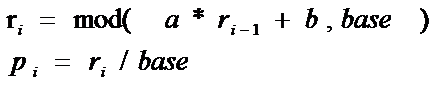
在这里采用一种方式生成随机数

其中i=1,2,3.。。。

而pi就是地推倒的第i个随机数

 

根据经验，一般选取基数base=256.0,一般为2的整数倍；另外的两个常数选取a=17.0 和b=139.0

 

需要注意

（1）这里的取模运算是针对浮点型数据的，而c语言中的取模运算不能用于浮点数数据的操作，这样就需要用户自己编写取模的程序；

（2）ri是随着递推而每次更新的。因此，如果将这个算法编写出函数，需要考虑参数是传值还是传地址；

 

递推更新，所以在这里要传地址，否则得不到结果！

#include <stdio.h>


double rand0_1(double *r)
{
    double base=256.0;
    double a=17.0;
    double b=139.0;
    double temp1=a*(*r)+b;
    //printf("%lf",temp1);
    double temp2=(int)(temp1/base); //得到余数
    double temp3=temp1-temp2*base;
    //printf("%lf
",temp2);
    //printf("%lf
",temp3);
    *r=temp3;
    double p=*r/base;
    return p;
}

int main()
{
    double r=5.0;
    printf("output 10 number between 0 and 1:
");
    for (int i = 0; i < 10; i++)
    {
        printf("%10.5lf
",rand0_1(&r));
    }
    return 0;
}

3 产生任意范围内的随机数，比如产生[m,n]之间的随机数

这个很容易，只要将之前的[0,1]之间的随机数这样处理就行了

m+(m-n)*rand0_1(&r)就行了；

 

#include <stdio.h>


double rand0_1(double *r)
{
    double base=256.0;
    double a=17.0;
    double b=139.0;
    double temp1=a*(*r)+b;
    //printf("%lf",temp1);
    double temp2=(int)(temp1/base); //得到余数
    double temp3=temp1-temp2*base;
    //printf("%lf
",temp2);
    //printf("%lf
",temp3);
    *r=temp3;
    double p=*r/base;
    return p;
}

int main()
{
    double m=1.0,n=5.0;
    double r=5.0;
    printf("output 10 number between 0 and 1:
");
    for (int i = 0; i < 10; i++)
    {
        printf("%10.5lf
",m+(n-m)*rand0_1(&r));
    }
    return 0;
}

4 正态分布的随机数生成算法

 

符合正太分布的随机数在研究中也很重要，下面给出一种生成正态分布数的方法

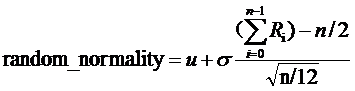
其中Ri表示[0,1]之间均匀分布的随机数；

 

u为均值，  为方差，当n趋向于无穷大的时候，得到随机的随机分布为正态分布；

#include <stdio.h>
#include <math.h>

double rand0_1(double *r)
{
      double base=256.0;
      double a=17.0;
      double b=139.0;
      double temp1=a*(*r)+b;
      //printf("%lf",temp1);
      double temp2=(int)(temp1/base); //得到余数
      double temp3=temp1-temp2*base;
      //printf("%lf
",temp2);
      //printf("%lf
",temp3);
      *r=temp3;
      double p=*r/base;
      return p;
}

double random_normality(double u,double t,double *r ,double n)
{
      double total=0.0;
      double result;
      for (int i = 0; i < n; i++)
      {
            total+=rand0_1(r);
      }
      result=u+t*(total-n/2)/sqrt(n/12);
      return result;
}

int main()
{
      double r=5.0;
      double u=2.0;
      double t=3.5;
      double n=12;
      printf("output 10 number between 0 and 1:
");
      for (int i = 0; i < 10; i++)
      {
            printf("%10.5lf
",random_normality(u,t,&r,n));
      }
      return 0;
}

上面设计的代码都已经运行通过！

 

 补充知识点：leveldb中使用了一个简单的方式来实现随机化数；算法的核心是seed_ = (seed_ * A) % M,

下面把源代码贴出来，不难，可以和上面的参考下

private:
  uint32_t seed_;
 public:
  explicit Random(uint32_t s) : seed_(s & 0x7fffffffu) {
    // Avoid bad seeds.
    if (seed_ == 0 || seed_ == 2147483647L) {
      seed_ = 1;
    }
  }
  uint32_t Next() {
    static const uint32_t M = 2147483647L;   // 2^31-1
    static const uint64_t A = 16807;  // bits 14, 8, 7, 5, 2, 1, 0
    // We are computing
    //       seed_ = (seed_ * A) % M,    where M = 2^31-1
    //
    // seed_ must not be zero or M, or else all subsequent computed values
    // will be zero or M respectively.  For all other values, seed_ will end
    // up cycling through every number in [1,M-1]
    uint64_t product = seed_ * A;

    // Compute (product % M) using the fact that ((x << 31) % M) == x.
    seed_ = static_cast<uint32_t>((product >> 31) + (product & M));
    // The first reduction may overflow by 1 bit, so we may need to
    // repeat.  mod == M is not possible; using > allows the faster
    // sign-bit-based test.
    if (seed_ > M) {
      seed_ -= M;
    }
    return seed_;
  }
  // Returns a uniformly distributed value in the range [0..n-1]
  // REQUIRES: n > 0
  uint32_t Uniform(int n) { return Next() % n; }

  // Randomly returns true ~"1/n" of the time, and false otherwise.
  // REQUIRES: n > 0
  bool OneIn(int n) { return (Next() % n) == 0; }

  // Skewed: pick "base" uniformly from range [0,max_log] and then
  // return "base" random bits.  The effect is to pick a number in the
  // range [0,2^max_log-1] with exponential bias towards smaller numbers.
  uint32_t Skewed(int max_log) {
    return Uniform(1 << Uniform(max_log + 1));
  }
};

这里面也直接取模得到一定范围内的随机数，简单明了。