拖了好久才写的线段树......
大概听说它可能实在n年前,在我还是一个孩子的时候[/微笑]
恩大概我觉得有一丢丢丢像分块
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
线段树,类似区间树,它在各个节点保存一条线段(数组中的一段子数组),主要用于高效解决连续区间的动态查询问题,由于二叉结构的特性,它基本能保持每个操作的复杂度为O(logn)。
线段树的每个节点表示一个区间,子节点则分别表示父节点的左右半区间,例如父亲的区间是[a,b],那么(c=(a+b)/2)左儿子的区间是[a,c],右儿子的区间是[c+1,b]。
下面我们从一个经典的例子来了解线段树,问题描述如下:从数组arr[0...n-1]中查找某个数组某个区间内的最小值,其中数组大小固定,但是数组中的元素的值可以随时更新。
对这个问题一个简单的解法是:遍历数组区间找到最小值,时间复杂度是O(n),额外的空间复杂度O(1)。当数据量特别大,而查询操作很频繁的时候,耗时可能会不满足需求。
另一种解法:使用一个二维数组来保存提前计算好的区间[i,j]内的最小值,那么预处理时间为O(n^2),查询耗时O(1), 但是需要额外的O(n^2)空间,当数据量很大时,这个空间消耗是庞大的,而且当改变了数组中的某一个值时,更新二维数组中的最小值也很麻烦。
我们可以用线段树来解决这个问题:预处理耗时O(n),查询、更新操作O(logn),需要额外的空间O(n)。根据这个问题我们构造如下的二叉树
- 叶子节点是原始组数arr中的元素
- 非叶子节点代表它的所有子孙叶子节点所在区间的最小值
例如对于数组[2, 5, 1, 4, 9, 3]可以构造如下的二叉树(背景为白色表示叶子节点,非叶子节点的值是其对应数组区间内的最小值,例如根节点表示数组区间arr[0...5]内的最小值 是1): 本文地址
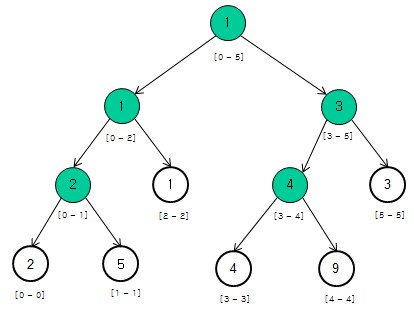
由于线段树的父节点区间是平均分割到左右子树,因此线段树是完全二叉树,对于包含n个叶子节点的完全二叉树,它一定有n-1个非叶节点,总共2n-1个节点,因此存储线段是需要的空间复杂度是O(n)。那么线段树的操作:创建线段树、查询、节点更新 是如何运作的呢(以下所有代码都是针对求区间最小值问题)?
1 struct SegTreeNode 2 { 3 int val; 4 }segTree[10010]; 5 //建建建 6 void build(int root,int arr[],int istart,iend) 7 { 8 if(istart==iend) 9 segTree[root].val=arr[istart]; 10 else 11 { 12 int mid=(istart+iend)/2; 13 build(root*2+1,arr,istart,mid); 14 build(root*2+2,arr,mid+1,iend); 15 segTree[root].val=min(segTree[root*2+1].val,segTree[root*2+2].val); 16 } 17 } 18 //单点查询 19 int query(int root,int nstart,int nend,int qstart,int qend) 20 { 21 if(nstart>qend || nend<qstart) 22 return INFINITE; 23 if(qstart<=nstart && qend>=nend) 24 return segTree[root].val; 25 int mid=(nstart+nend)/2; 26 return min(query(root*2+1,nstart,mid,qstart,qend),query(root*2+2,mid+1,nend,qstart,qend)); 27 } 28 //单点更新 29 void update(int root,int nstart,int nend,int index,int addval) 30 { 31 if(nstart==nend) 32 { 33 if(nstart==index)segTree[index].val+=addval; 34 return; 35 } 36 int mid=(nstart+nend)/2; 37 if(index<=mid)update(root*2+1,nstart,mid,index,addval); 38 else update(root*2+2,mid+1,nend,index,addval); 39 segTree[root].val=min(segTree[2*root+1].val,segTree[2*root+2].val); 40 }
以及区间
1 const int INFINITE = INT_MAX; 2 const int MAXNUM = 1000; 3 struct SegTreeNode 4 { 5 int val; 6 int addMark;//延迟标记 7 }segTree[MAXNUM];//定义线段树 8 9 /* 10 功能:构建线段树 11 root:当前线段树的根节点下标 12 arr: 用来构造线段树的数组 13 istart:数组的起始位置 14 iend:数组的结束位置 15 */ 16 void build(int root, int arr[], int istart, int iend) 17 { 18 segTree[root].addMark = 0;//----设置标延迟记域 19 if(istart == iend)//叶子节点 20 segTree[root].val = arr[istart]; 21 else 22 { 23 int mid = (istart + iend) / 2; 24 build(root*2+1, arr, istart, mid);//递归构造左子树 25 build(root*2+2, arr, mid+1, iend);//递归构造右子树 26 //根据左右子树根节点的值,更新当前根节点的值 27 segTree[root].val = min(segTree[root*2+1].val, segTree[root*2+2].val); 28 } 29 } 30 31 /* 32 功能:当前节点的标志域向孩子节点传递 33 root: 当前线段树的根节点下标 34 */ 35 void pushDown(int root) 36 { 37 if(segTree[root].addMark != 0) 38 { 39 //设置左右孩子节点的标志域,因为孩子节点可能被多次延迟标记又没有向下传递 40 //所以是 “+=” 41 segTree[root*2+1].addMark += segTree[root].addMark; 42 segTree[root*2+2].addMark += segTree[root].addMark; 43 //根据标志域设置孩子节点的值。因为我们是求区间最小值,因此当区间内每个元 44 //素加上一个值时,区间的最小值也加上这个值 45 segTree[root*2+1].val += segTree[root].addMark; 46 segTree[root*2+2].val += segTree[root].addMark; 47 //传递后,当前节点标记域清空 48 segTree[root].addMark = 0; 49 } 50 } 51 52 /* 53 功能:线段树的区间查询 54 root:当前线段树的根节点下标 55 [nstart, nend]: 当前节点所表示的区间 56 [qstart, qend]: 此次查询的区间 57 */ 58 int query(int root, int nstart, int nend, int qstart, int qend) 59 { 60 //查询区间和当前节点区间没有交集 61 if(qstart > nend || qend < nstart) 62 return INFINITE; 63 //当前节点区间包含在查询区间内 64 if(qstart <= nstart && qend >= nend) 65 return segTree[root].val; 66 //分别从左右子树查询,返回两者查询结果的较小值 67 pushDown(root); //----延迟标志域向下传递 68 int mid = (nstart + nend) / 2; 69 return min(query(root*2+1, nstart, mid, qstart, qend), 70 query(root*2+2, mid + 1, nend, qstart, qend)); 71 72 } 73 74 /* 75 功能:更新线段树中某个区间内叶子节点的值 76 root:当前线段树的根节点下标 77 [nstart, nend]: 当前节点所表示的区间 78 [ustart, uend]: 待更新的区间 79 addVal: 更新的值(原来的值加上addVal) 80 */ 81 void update(int root, int nstart, int nend, int ustart, int uend, int addVal) 82 { 83 //更新区间和当前节点区间没有交集 84 if(ustart > nend || uend < nstart) 85 return ; 86 //当前节点区间包含在更新区间内 87 if(ustart <= nstart && uend >= nend) 88 { 89 segTree[root].addMark += addVal; 90 segTree[root].val += addVal; 91 return ; 92 } 93 pushDown(root); //延迟标记向下传递 94 //更新左右孩子节点 95 int mid = (nstart + nend) / 2; 96 update(root*2+1, nstart, mid, ustart, uend, addVal); 97 update(root*2+2, mid+1, nend, ustart, uend, addVal); 98 //根据左右子树的值回溯更新当前节点的值 99 segTree[root].val = min(segTree[root*2+1].val, segTree[root*2+2].val); 100 }