一 kNN算法简介
kNN(K-Nearest Neighbor)工作原理:存在一个样本数据集合,也称为训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一数据与所属分类对应的关系。输入没有标签的数据后,将新数据中的每个特征与样本集中数据对应的特征进行比较,提取出样本集中特征最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k近邻算法中k的出处,通常k是不大于20的整数。最后选择k个最相似数据中出现次数最多的分类作为新数据的分类。
说明:KNN没有显示的训练过程,它是“懒惰学习”的代表,它在训练阶段只是把数据保存下来,训练时间开销为0,等收到测试样本后进行处理。
优点:
- 解决分类问题
- 天然可以解决多分类问题
- 思想简单,要过强大
缺点:
- 最大的缺点
如果训练集有m个样本,n个特征,则预测每一个新的数据,需要O(m*n)
优化:使用树结构:KD-Tree, Ball-Tree
- 高度数据相关
- 预测的结果不具有可解释性
- 维数灾难
随着维数的增加,看似两个距离非常近的点,距离会越来越大。所以kNN不适合高维度的数据,解决方法:PCA 降维处理
二 一个简单的例子
现有十组肿瘤数据,raw_data_x 分别是肿瘤大小和肿瘤时间,raw_data_y代表的是 良性肿瘤和恶性肿瘤,x代表的是测试数据,并用蓝色区分,我们需要通过kNN算法判断其实良性肿瘤还是恶性肿瘤。通过matplotlib绘制散点图如下:
import numpy as np
import matplotlib.pyplot as plt
raw_data_x = [[3.393533211,2.331273381],
[3.110073483,1.781539638],
[1.343808831,3.368360954],
[3.582294042,4.679179110],
[2.280362439,2.866990263],
[7.423436942,4.696522875],
[5.745051997,3.533989803],
[9.172168622,2.511101045],
[7.792783481,3.424088941],
[7.939820817,0.791637231]]
raw_data_y = [0,0,0,0,0,1,1,1,1,1]
x = np.array([8.093607318,3.365731514])
x_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)
plt.scatter(x_train[y_train==0,0],x_train[y_train==0,1],color='g')
plt.scatter(x_train[y_train==1,0],x_train[y_train==1,1],color='r')
plt.scatter(x[0],x[1],color='b')
plt.show()
运行结果:

上图中 绿色为良性肿瘤,红色为恶性肿瘤,蓝色为需要判断的样本。
整体思路为:
1、计算每个样本与蓝点的距离
2、将计算出来的距离进行排序
3、取出前k个样本
4、统计前k个样本中出现频率最多的种类
5、输出判断结果
说明:这里的距离指得是 明可夫斯基距离
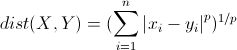
根据以上思路,可以编写一下代码:
import numpy as np import matplotlib.pyplot as plt raw_data_x = [[3.393533211,2.331273381], [3.110073483,1.781539638], [1.343808831,3.368360954], [3.582294042,4.679179110], [2.280362439,2.866990263], [7.423436942,4.696522875], [5.745051997,3.533989803], [9.172168622,2.511101045], [7.792783481,3.424088941], [7.939820817,0.791637231]] raw_data_y = [0,0,0,0,0,1,1,1,1,1] x = np.array([8.093607318,3.365731514]) x_train = np.array(raw_data_x) y_train = np.array(raw_data_y) plt.scatter(x_train[y_train==0,0],x_train[y_train==0,1],color='g') plt.scatter(x_train[y_train==1,0],x_train[y_train==1,1],color='r') plt.scatter(x[0],x[1],color='b') plt.show() # 在原有基础上添加以下代码 from math import sqrt from collections import Counter # 计算每个样本到目标的距离 distances = [sqrt(np.sum((e-x)**2)) for e in x_train] #将计算的距离进行排序,并返回对应的索引 nearest = np.argsort(distances) # 取前6个样本 k = 6 # 将最近的k个样本取出来,topK_y 中为样本种类 topK_y = [y_train[i] for i in nearest[:k]] # 统计topK_y中的种类和数量 votes = Counter(topK_y) # 获取最多数量的样本 votes.most_common(1) # 获取最多样本的种类 predict_y = votes.most_common(1)[0][0] print("肿瘤类型:",predict_y)
运行结果:

肿瘤类型: 1
以上就是通过kNN算法进行类型判断的简易过程。
三 使用scikit-learn中的kNN
有了以上的基础,使用scikit-learn中的kNN应该就比较容易了。
from sklearn.neighbors import KNeighborsClassifier import numpy as np import matplotlib.pyplot as plt raw_data_x = [[3.393533211,2.331273381], [3.110073483,1.781539638], [1.343808831,3.368360954], [3.582294042,4.679179110], [2.280362439,2.866990263], [7.423436942,4.696522875], [5.745051997,3.533989803], [9.172168622,2.511101045], [7.792783481,3.424088941], [7.939820817,0.791637231]] raw_data_y = [0,0,0,0,0,1,1,1,1,1] x_train = np.array(raw_data_x) y_train = np.array(raw_data_y) x = np.array([8.093607318,3.365731514]) # 生成一个k为6 kNN的对象 kNN_classifier = KNeighborsClassifier(n_neighbors=6) # 将训练数据写入 kNN_classifier.fit(x_train,y_train) # 预测数据 y_predict = kNN_classifier.predict(x.reshape(1,-1)) # 输出预测结果 print(y_predict )
需要详细描述,查看 官方文档