描述
Alice and Bob are walking in an ancient maze with a lot of caves and one-way passages connecting them. They want to go from cave 1 to cave n. All the passages are difficult to pass. Passages are too small for two people to walk through simultaneously, and crossing a passage can make it even more difficult to pass for the next person. We define di as the difficulty of crossing passage i for the first time, and ai as the additional difficulty for the second time (e.g. the second person's difficulty is di+ai).
Your task is to find two (possibly identical) routes for Alice and Bob, so that their total difficulty is minimized.
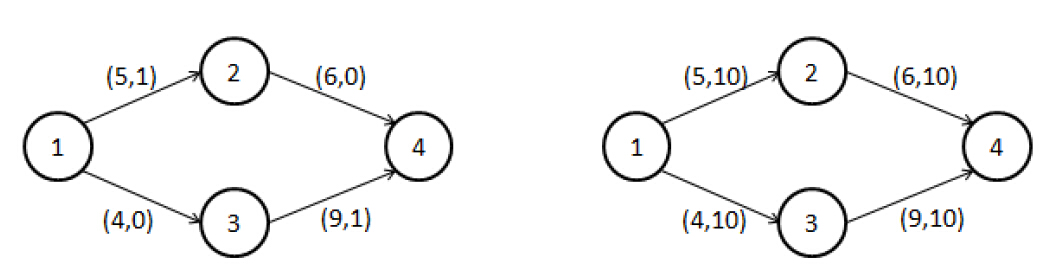
For example, in figure 1, the best solution is 1->2->4 for both Alice and Bob, but in figure 2, it's better to use 1->2->4 for Alice and 1->3->4 for Bob.
输入
There will be at most 200 test cases. Each case begins with two integers n, m (1<=n<=500, 1<=m<=2000), the number of caves and passages. Each of the following m lines contains four integers u, v, di and ai (1<=u,v<=n, 1<=di<=1000, 0<=ai<=1000). Note that there can be multiple passages connecting the same pair of caves, and even passages connecting a cave and itself.
输出
For each test case, print the case number and the minimal total difficulty.
样例输入
4 4
1 2 5 1
2 4 6 0
1 3 4 0
3 4 9 1
4 4
1 2 5 10
2 4 6 10
1 3 4 10
3 4 9 10
样例输出
Case 1: 23
Case 2: 24
题意
找两条从1到N的路使得总花费最小,一条路第一次走花费d,第二次走花费d+a
题解
每个点建两条边一条流量1花费d,一条流量1花费d+a
源点S=0,和1连一条边流量2花费0
汇点T=n+1,和n连一条边流量2花费0
然后跑一边最小费用最大流
代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 4 const int N=1e5+5; 5 const int M=2e5+5; 6 const int INF=0x3f3f3f3f; 7 8 int FIR[N],FROM[M],TO[M],CAP[M],FLOW[M],COST[M],NEXT[M],tote; 9 int pre[N],dist[N],q[400000]; 10 bool vis[N]; 11 int n,m,S,T; 12 void init() 13 { 14 tote=0; 15 memset(FIR,-1,sizeof(FIR)); 16 } 17 void addEdge(int u,int v,int cap,int cost) 18 { 19 FROM[tote]=u; 20 TO[tote]=v; 21 CAP[tote]=cap; 22 FLOW[tote]=0; 23 COST[tote]=cost; 24 NEXT[tote]=FIR[u]; 25 FIR[u]=tote++; 26 27 FROM[tote]=v; 28 TO[tote]=u; 29 CAP[tote]=0; 30 FLOW[tote]=0; 31 COST[tote]=-cost; 32 NEXT[tote]=FIR[v]; 33 FIR[v]=tote++; 34 } 35 bool SPFA(int s, int t) 36 { 37 memset(dist,INF,sizeof(dist)); 38 memset(vis,false,sizeof(vis)); 39 memset(pre,-1,sizeof(pre)); 40 dist[s] = 0;vis[s]=true;q[1]=s; 41 int head=0,tail=1; 42 while(head!=tail) 43 { 44 int u=q[++head];vis[u]=false; 45 for(int v=FIR[u];v!=-1;v=NEXT[v]) 46 { 47 if(dist[TO[v]]>dist[u]+COST[v]&&CAP[v]>FLOW[v]) 48 { 49 dist[TO[v]]=dist[u]+COST[v]; 50 pre[TO[v]]=v; 51 if(!vis[TO[v]]) 52 { 53 vis[TO[v]] = true; 54 q[++tail]=TO[v]; 55 } 56 } 57 } 58 } 59 return pre[t]!=-1; 60 } 61 void MCMF(int s, int t, int &cost, int &flow) 62 { 63 flow=0; 64 cost=0; 65 while(SPFA(s,t)) 66 { 67 int Min = INF; 68 for(int v=pre[t];v!=-1;v=pre[TO[v^1]]) 69 Min = min(Min, CAP[v]-FLOW[v]); 70 for(int v=pre[t];v!=-1;v=pre[TO[v^1]]) 71 { 72 FLOW[v]+=Min; 73 FLOW[v^1]-=Min; 74 cost+=COST[v]*Min; 75 } 76 flow+=Min; 77 } 78 } 79 int main() 80 { 81 int ca=0; 82 while(scanf("%d%d",&n,&m)!= EOF) 83 { 84 init(); 85 for(int i=0,u,v,d,a;i<m;i++) 86 { 87 scanf("%d%d%d%d",&u,&v,&d,&a); 88 addEdge(u,v,1,d); 89 addEdge(u,v,1,d+a); 90 } 91 S=0,T=n+1; 92 addEdge(S,1,2,0); 93 addEdge(n,T,2,0); 94 int cost,flow; 95 MCMF(S,T,cost,flow); 96 printf("Case %d: %d ",++ca,cost); 97 } 98 return 0; 99 }