勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。在中国,商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例。在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。相传毕达哥拉斯所在的学校为了庆祝他证明了这个定理,特意举行了一个盛大的宴会,吃掉了一百头牛,所以西方也戏称该定理为“百牛定理”。
关于定理的证明有很多种,下面介绍几何原本中的毕达哥拉斯证明方法。
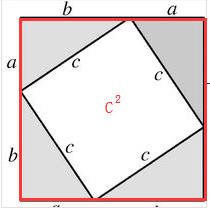
如图所示,假设直角三角形的直角边和斜边分别是a、b和c。
图中外面大的正方形边长为a+b, 内部是四个全等的、边长为a、b和C的直角三角形,以及一个边长为c的正方形。外面正方形的面积为:
$$ (a+b)^2 = a^2+b^2+2ab $$
内部四个直角三角形和正方形的面积之和为:
$$ c^2+2ab $$
由于同一个正方形(外面的)的面积一定相等,因此:
$$ a^2+b^2+2ab = c^2+2ab $$
即:
$$ a^2 + b^2 = c^2 $$