原文链接:http://tecdat.cn/?p=3429
BART是贝叶斯非参数模型,可以使用Backfitting MCMC进行拟合 。
我不使用任何软件包...... MCMC是从头开始实现的。
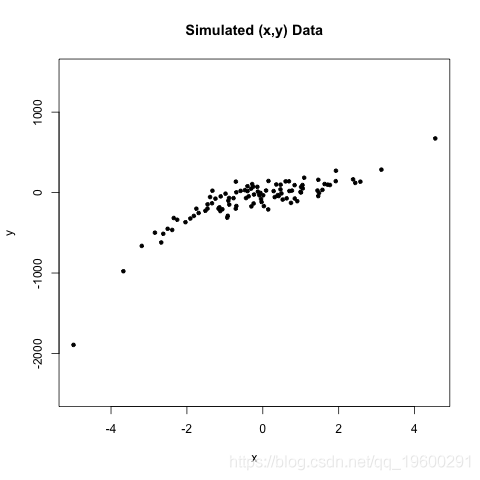
考虑协变量数据
我们可能会考虑以下概率模型
基本上我们使用三次多项式对条件均值进行建模。请注意,这是更一般的添加剂模型的特例
在这种情况下
每个条件后验
直观地,
在正常之前
Backfitting MCMC如下进行。首先,初始化所有测试版除外
- 计算
- 计算
- 对所有beta参数继续此过程。
术语反向拟合似乎是合适的,因为在每次迭代中,我们都“退出”
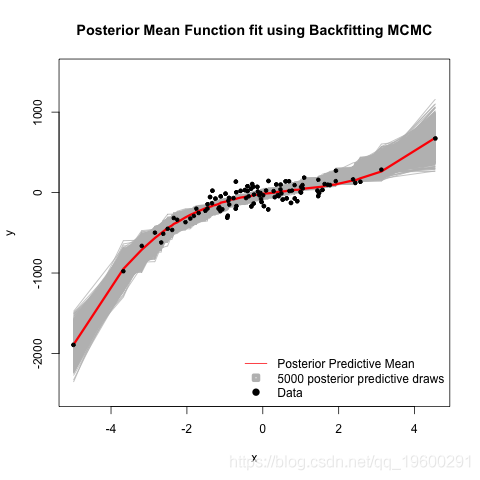
为了获得拟合的回归线,我们需要从后验预测分布中进行采样。我们在每个Gibbs迭代中的步骤4之后通过绘制
上标