原文链接:http://tecdat.cn/?p=9529
目录
怎么做测试
具有两个类别和II型平方和的协方差示例的分析
本示例使用II型平方和 。参数估计值在R中的计算方式不同,
Data = read.table(textConnection(Input),header=TRUE)
plot(x = Data$Temp,
y = Data$Pulse,
col = Data$Species,
pch = 16,
xlab = "Temperature",
ylab = "Pulse")
legend('bottomright',
legend = levels(Data$Species),
col = 1:2,
cex = 1,
pch = 16)协方差分析
Anova Table (Type II tests)
Sum Sq Df F value Pr(>F)
Temp 4376.1 1 1388.839 < 2.2e-16 ***
Species 598.0 1 189.789 9.907e-14 ***
Temp:Species 4.3 1 1.357 0.2542
### Interaction is not significant, so the slope across groups
### is not different.
model.2 = lm (Pulse ~ Temp + Species,
data = Data)
library(car)
Anova(model.2, type="II")
Anova Table (Type II tests)
Sum Sq Df F value Pr(>F)
Temp 4376.1 1 1371.4 < 2.2e-16 ***
Species 598.0 1 187.4 6.272e-14 ***
### The category variable (Species) is significant,
### so the intercepts among groups are different
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7.21091 2.55094 -2.827 0.00858 **
Temp 3.60275 0.09729 37.032 < 2e-16 ***
Speciesniv -10.06529 0.73526 -13.689 6.27e-14 ***
### but the calculated results will be identical.
### The slope estimate is the same.
### The intercept for species 1 (ex) is (intercept).
### The intercept for species 2 (niv) is (intercept) + Speciesniv.
### This is determined from the contrast coding of the Species
### variable shown below, and the fact that Speciesniv is shown in
### coefficient table above.
niv
ex 0
niv 1拟合线的简单图解
plot(x = Data$Temp,
y = Data$Pulse,
col = Data$Species,
pch = 16,
xlab = "Temperature",
ylab = "Pulse")
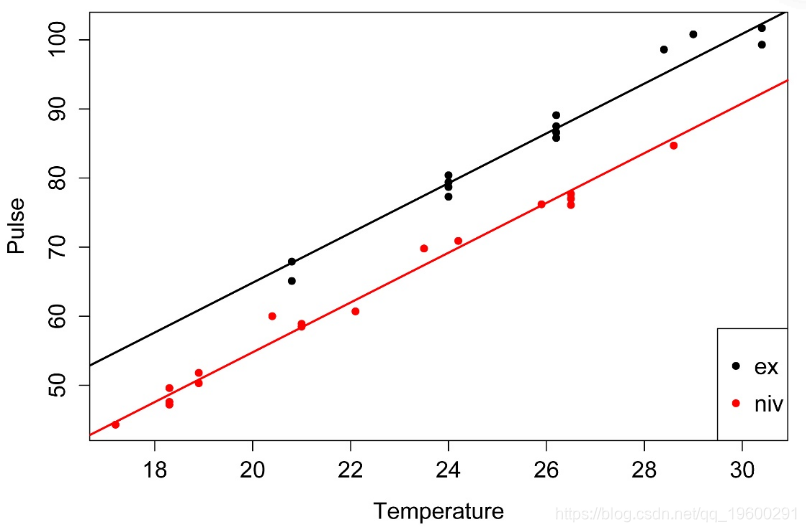
模型的p值和R平方
Multiple R-squared: 0.9896, Adjusted R-squared: 0.9888
F-statistic: 1331 on 2 and 28 DF, p-value: < 2.2e-16检查模型的假设
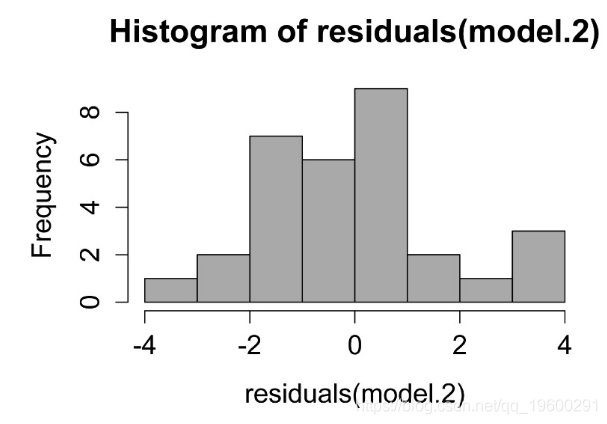
线性模型中残差的直方图。这些残差的分布应近似正态。
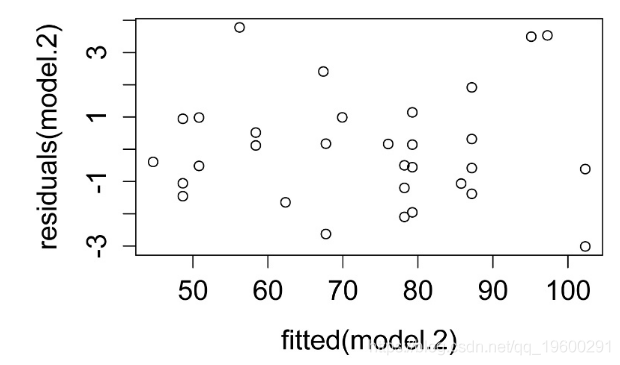
残差与预测值的关系图。残差应无偏且均等。
### additional model checking plots with: plot(model.2)
### alternative: library(FSA); residPlot(model.2)
具有三类和II型平方和的协方差示例分析
本示例使用II型平方和,并考虑具有三个组的情况。
### --------------------------------------------------------------
### Analysis of covariance, hypothetical data
### --------------------------------------------------------------
Data = read.table(textConnection(Input),header=TRUE)plot(x = Data$Temp,
y = Data$Pulse,
col = Data$Species,
pch = 16,
xlab = "Temperature",
ylab = "Pulse")
legend('bottomright',
legend = levels(Data$Species),
col = 1:3,
cex = 1,
pch = 16)协方差分析
options(contrasts = c("contr.treatment", "contr.poly"))
### These are the default contrasts in R
Anova(model.1, type="II")
Sum Sq Df F value Pr(>F)
Temp 7026.0 1 2452.4187 <2e-16 ***
Species 7835.7 2 1367.5377 <2e-16 ***
Temp:Species 5.2 2 0.9126 0.4093
### Interaction is not significant, so the slope among groups
### is not different.
Anova(model.2, type="II")
Sum Sq Df F value Pr(>F)
Temp 7026.0 1 2462.2 < 2.2e-16 ***
Species 7835.7 2 1373.0 < 2.2e-16 ***
Residuals 125.6 44
### The category variable (Species) is significant,
### so the intercepts among groups are different
summary(model.2)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.35729 1.90713 -3.333 0.00175 **
Temp 3.56961 0.07194 49.621 < 2e-16 ***
Speciesfake 19.81429 0.66333 29.871 < 2e-16 ***
Speciesniv -10.18571 0.66333 -15.355 < 2e-16 ***
### The slope estimate is the Temp coefficient.
### The intercept for species 1 (ex) is (intercept).
### The intercept for species 2 (fake) is (intercept) + Speciesfake.
### The intercept for species 3 (niv) is (intercept) + Speciesniv.
### This is determined from the contrast coding of the Species
### variable shown below.
contrasts(Data$Species)
fake niv
ex 0 0
fake 1 0
niv 0 1拟合线的简单图解
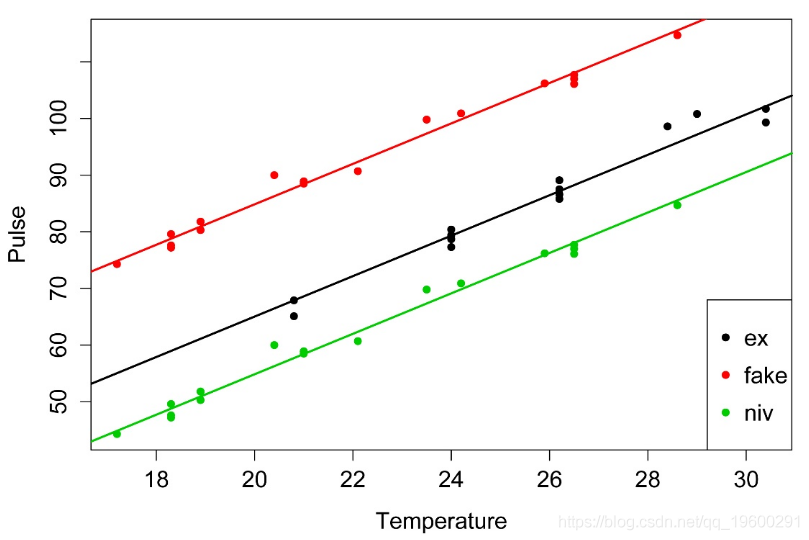
组合模型的p值和R平方
Multiple R-squared: 0.9919, Adjusted R-squared: 0.9913
F-statistic: 1791 on 3 and 44 DF, p-value: < 2.2e-16检查模型的假设
hist(residuals(model.2),
col="darkgray") 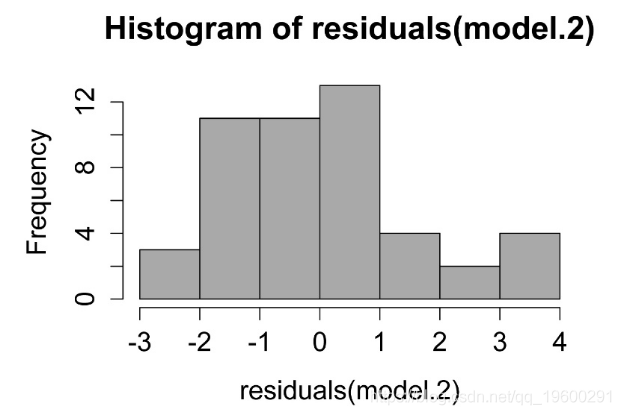
线性模型中残差的直方图。这些残差的分布应近似正态。
plot(fitted(model.2),
residuals(model.2)) 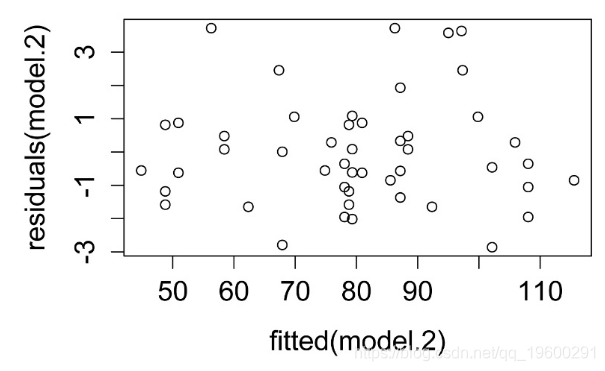
残差与预测值的关系图。残差应无偏且均等。
### additional model checking plots with: plot(model.2)
### alternative: library(FSA); residPlot(model.2)