原文链接：http://tecdat.cn/?p=10148
今天的主题是Stata中的治疗效果功能。
治疗效果估算器根据观察数据估算治疗对结果的因果关系。
我们将讨论四种治疗效果估计量：
- RA：回归调整
- IPW：逆概率加权
- IPWRA：具有回归调整的逆概率加权
- AIPW：增强的逆概率加权
我们将保存第2部分的匹配估算器。
与对观测数据进行的任何回归分析一样，因果关系的解释必须基于合理的基础科学原理。
介绍
我们将讨论治疗方法和结果。
一种治疗可能是新药，其结果是血压或胆固醇水平升高。治疗可以是外科手术，也可以是患者活动的结局。治疗可以是职业培训计划以及结果就业或工资。待遇甚至可以是旨在提高产品销量的广告系列。
考虑一下母亲吸烟是否会影响婴儿出生时的体重。只能使用观测数据来回答这样的问题。
观察数据的问题是受试者选择是否接受治疗。例如，母亲决定吸烟还是不吸烟。据说这些受试者已自我选择进入治疗组和未治疗组。
在理想的世界中，我们将设计一个实验来测试因果关系和治疗结局之间的关系。我们将受试者随机分配到治疗组或未治疗组。随机分配治疗方法可确保治疗方法与结果无关，从而大大简化了分析。
因果推论要求对每个治疗水平的结果的无条件估计。无论数据是观察性的还是实验性的，我们仅观察以接受治疗为条件的每个受试者的结局。对于实验数据，治疗的随机分配保证了治疗与结果无关。因此，以观察到的治疗为条件的平均结果可估算出无条件的关注手段。对于观察数据，我们对治疗分配过程进行建模。如果我们的模型是正确的，则根据我们模型中的协变量，治疗分配过程被认为与随机条件一样好。
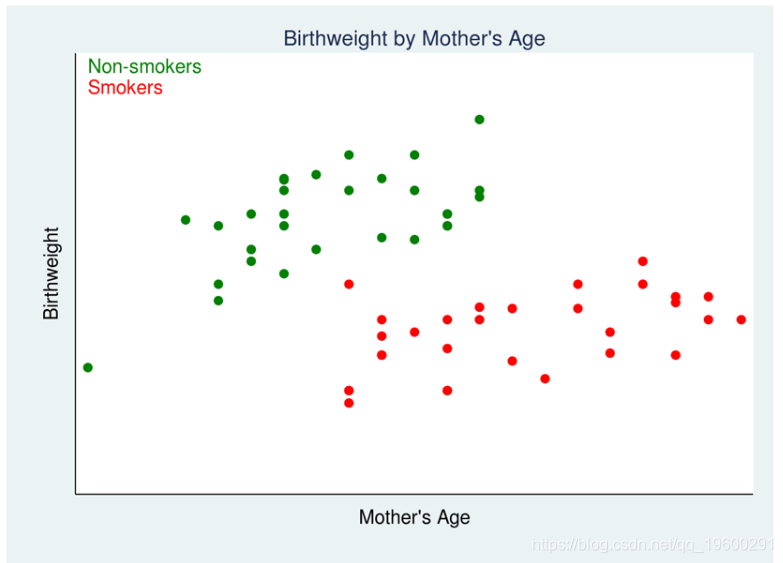
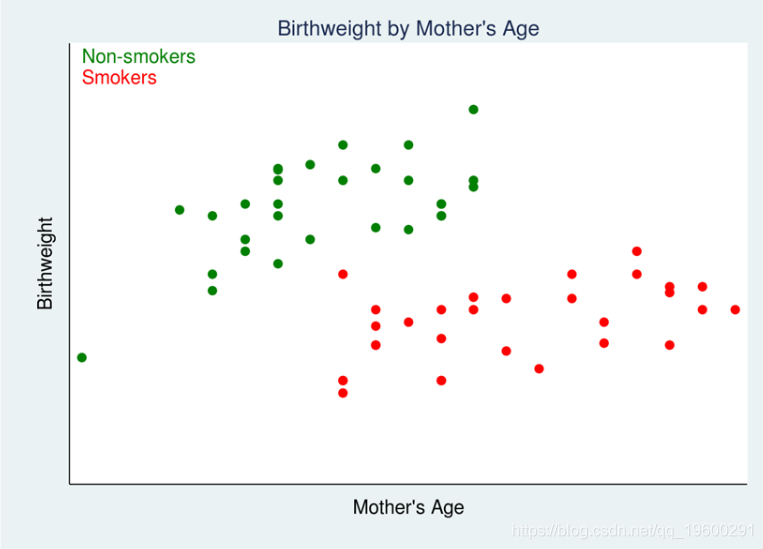
让我们考虑一个例子。图1是类似于Cattaneo（2010）使用的观测数据的散点图。治疗变量是母亲在怀孕期间的吸烟状况，结果是婴儿的出生体重。
红点表示怀孕期间吸烟的母亲，而绿点表示未怀孕的母亲。母亲自己选择是否吸烟，这使分析变得复杂。
我们不能通过比较吸烟和不吸烟的母亲的平均出生体重来估计吸烟对出生体重的影响。为什么不？再看一下我们的图表。年龄较大的母亲往往体重较重，无论怀孕时是否吸烟。在这些数据中，年龄较大的母亲也更有可能吸烟。因此，母亲的年龄与治疗状况和结局有关。那么我们应该如何进行呢？
RA：回归调整估计量
RA估计量对结果进行建模，以说明非随机治疗分配。
我们可能会问：“如果吸烟的母亲选择不吸烟，结果将如何改变？”或“如果不吸烟的母亲选择吸烟，结果将会如何改变？”。如果我们知道这些反事实问题的答案，那么分析将很容易：我们只需从反事实结果中减去观察到的结果即可。
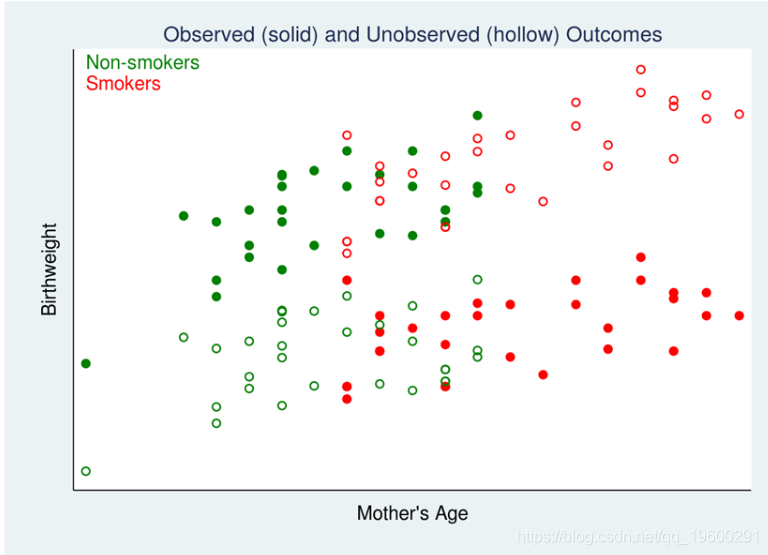
我们可以构建对这些未观察到的潜在结果的度量，我们的数据可能看起来像这样：
在图2中，使用实心点显示观察到的数据，而使用空心点显示未观察到的潜在结果。空心的红点代表吸烟者不吸烟的潜在后果。空心的绿色点代表不吸烟者吸烟的潜在后果。
我们可以通过将单独的线性回归模型与观察到的数据（实点）拟合到两个治疗组，从而估计未观察到的潜在结果。
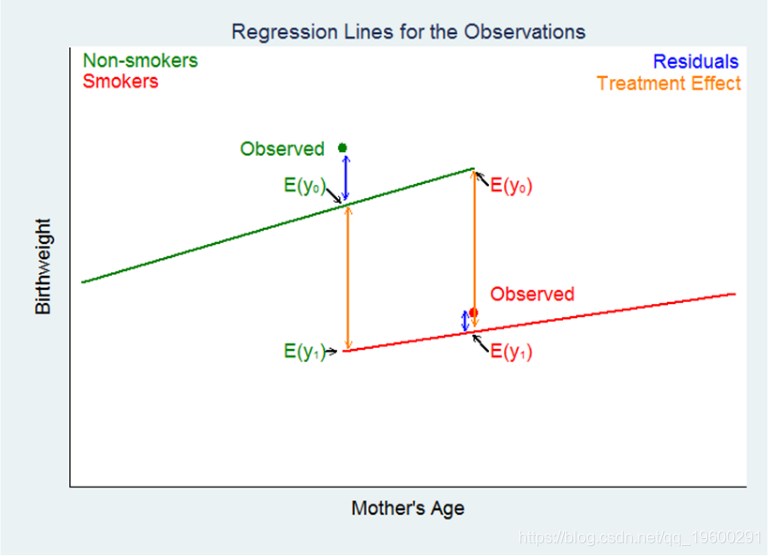
在图3中，我们为不吸烟者提供了一条回归线（绿线），为吸烟者提供了一条单独的回归线（红线）。
让我们了解这两行的含义：
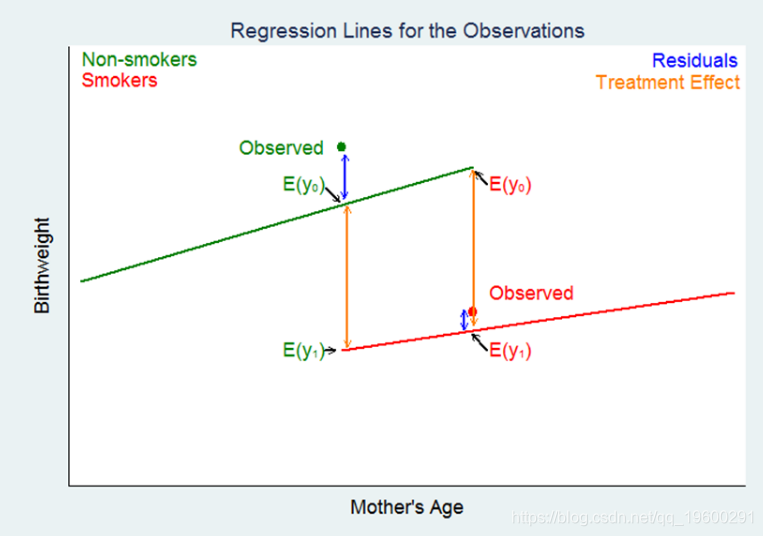
图4左侧标记为“已观察 ”的绿点是对不吸烟的母亲的观察。绿色回归线上标有E（y0）的点是考虑到母亲的年龄并且不吸烟的婴儿的预期出生体重。红色回归线上标有E（y1）的点是同一名母亲吸烟后婴儿的预期出生体重。
这些期望之间的差异估计了未接受治疗者的协变量特异性治疗效果。
现在，让我们看看另一个反事实问题。
图4右侧的红色标记为“ 观察到的红色”是对怀孕期间吸烟的母亲的观察。绿色和红色回归线上的点再次表示在两种治疗条件下母亲婴儿的预期出生体重（潜在的结局）。
这些期望之间的差异估计了接受治疗者的协变量特异性治疗效果。
请注意，我们根据每个变量的协变量值来估计平均治疗效果（ATE）。此外，无论实际接受哪种治疗，我们都对每位受试者估计这种效果。数据中所有受试者的这些效应的平均值估计了ATE。
我们还可以使用图4来激发对每个受试者在每种治疗水平下可获得的结果的预测，而与所接受的治疗无关。这个故事类似于上面的故事。数据中所有受试者的这些预测值的平均值估计每个治疗水平的潜在结果均值（POM）。
估计的POM的差异与上述ATE的估计相同。
被治疗者（ATET）上的ATE与ATE相似，但仅使用在治疗组中观察到的受试者。这种计算治疗效果的方法称为回归调整（RA）。
. webuse cattaneo2.dta, clear
(Excerpt from Cattaneo (2010) Journal of Econometrics 155: 138-154)
To estimate the POMs in the two treatment groups, we type
. teffects ra (bweight mage) (mbsmoke), pomeans 我们在第一组括号中指定结果模型，并带有结果变量及其后的协变量。在此示例中，结果变量为bweight，唯一的协变量为mage。
我们在第二组括号中指定处理模型（仅是处理变量）。在此示例中，我们仅指定处理变量mbsmoke。我们将在下一节中讨论协变量。
键入命令的结果是
Iteration 0: EE criterion = 7.878e-24
Iteration 1: EE criterion = 8.468e-26
Treatment-effects estimation Number of obs = 4642
Estimator : regression adjustment
Outcome model : linear
Treatment model: none
------------------------------------------------------------------------------
| Robust
bweight | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
POmeans |
mbsmoke |
nonsmoker | 3409.435 9.294101 366.84 0.000 3391.219 3427.651
smoker | 3132.374 20.61936 151.91 0.000 3091.961 3172.787
------------------------------------------------------------------------------输出报告说，如果所有母亲吸烟，平均出生体重将为3132克，如果没有母亲吸烟，则平均出生体重将为3409克。
我们可以通过减去POM来估算出生体重时吸烟的ATE：3132.374 – 3409.435 = -277.061。或者，我们可以使用ate选项重新发出teffects ra命令，并获取标准错误和置信区间：
Iteration 0: EE criterion = 7.878e-24
Iteration 1: EE criterion = 5.185e-26
Treatment-effects estimation Number of obs = 4642
Estimator : regression adjustment
Outcome model : linear
Treatment model: none
-------------------------------------------------------------------------------
| Robust
bweight | Coef. Std. Err. z P>|z| [95% Conf. Interval]
--------------+----------------------------------------------------------------
ATE |
mbsmoke |
(smoker vs |
nonsmoker) | -277.0611 22.62844 -12.24 0.000 -321.4121 -232.7102
--------------+----------------------------------------------------------------
POmean |
mbsmoke |
nonsmoker | 3409.435 9.294101 366.84 0.000 3391.219 3427.651
-------------------------------------------------------------------------------输出报告的是我们手动计算的相同ATE：-277.061。ATE是每个母亲吸烟时出生体重与没有母亲吸烟时出生体重之间差异的平均值。
IPW：逆概率加权估计器
RA估计量对结果进行建模，以说明非随机治疗分配。一些研究人员更喜欢为治疗分配过程建模，而不为结果指定模型。
我们知道，在我们的数据中，吸烟者往往比不吸烟者年龄大。我们还假设母亲的年龄直接影响出生体重。我们在图1中观察到了这一点 。
该图显示治疗分配取决于母亲的年龄。我们希望有一种调整这种依赖性的方法。特别是，我们希望我们有更多的较高年龄的绿色点和较低年龄的红色点。如果这样做的话，每组的平均出生体重将会改变。我们不知道这将如何影响均值差异，但是我们知道这将是对差异的更好估计。
为了获得类似的结果，我们将对较低年龄段的吸烟者和较高年龄段的不吸烟者进行加权，而对较高年龄段的吸烟者和较低年龄段中的不吸烟者进行加权。
我们将采用以下形式的概率模型或logit模型
Pr（女人抽烟）= F（a + b *年龄）
teffects默认使用logit，但是我们将指定probit选项进行说明。
一旦我们拟合了该模型，就可以为数据中的每个观察获得预测Pr（女人抽烟）。我们称这个为p i。然后，在进行POM计算（这只是平均值计算）时，我们将使用这些概率对观测值进行加权。我们将对吸烟者的观测值加权为1 / p i，以便当成为吸烟者的可能性较小时，权重将较大。我们将对不吸烟者的观察加权1 /（1- p i），以便当不吸烟者的概率较小时，权重将较大。
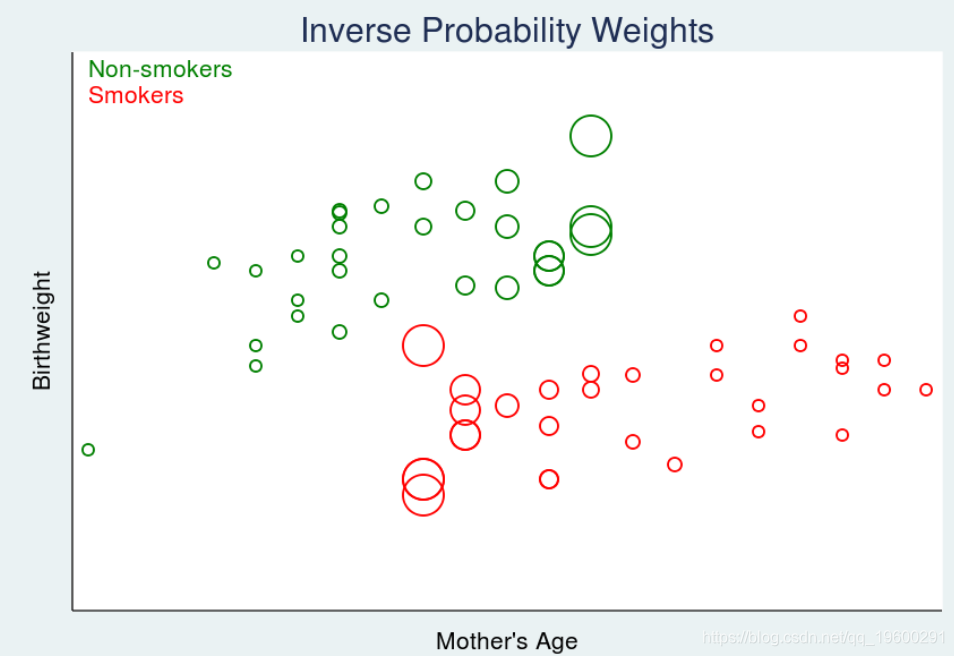
结果是下图替换了图1：
在图5中，较大的圆圈表示较大的权重。
要使用此IPW估算器估算POM，我们可以输入
第一组括号指定结果模型，在这种情况下，它只是结果变量。没有协变量。第二组括号指定处理模型，其中包括结果变量（mbsmoke），后跟协变量（在这种情况下，仅是mage）和模型的类型（probit）。
结果是
Iteration 0: EE criterion = 3.615e-15
Iteration 1: EE criterion = 4.381e-25
Treatment-effects estimation Number of obs = 4642
Estimator : inverse-probability weights
Outcome model : weighted mean
Treatment model: probit
------------------------------------------------------------------------------
| Robust
bweight | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
POmeans |
mbsmoke |
nonsmoker | 3408.979 9.307838 366.25 0.000 3390.736 3427.222
smoker | 3133.479 20.66762 151.61 0.000 3092.971 3173.986
------------------------------------------------------------------------------我们的输出报告说，如果所有母亲吸烟，平均出生体重将为3133克，如果没有母亲吸烟，则平均出生体重将为3409克。
这次，ATE是-275.5，如果我们键入
(Output omitted)我们将了解到标准误为22.68，95％置信区间为[-319.9,231.0]。
就像使用teffects ra一样，如果我们需要ATET，则可以使用atet选项指定teffects ipw命令。
IPWRA：具有回归调整估计量的IPW
RA估计量对结果进行建模，以说明非随机治疗分配。IPW估算器对处理进行建模以说明非随机处理分配。IPWRA估算器对结果和治疗方法进行建模，以说明非随机治疗方案。
IPWRA使用IPW权重来估计校正后的回归系数，随后将其用于执行回归调整。
结局模型和治疗模型中的协变量不必相同，它们常常不是因为影响受试者选择治疗组的变量通常不同于与结果相关的变量。IPWRA估算器具有双重鲁棒性，这意味着如果错误指定了治疗模型或结果模型（而不是两者），则效果的估算将保持一致。
让我们考虑具有更复杂的结果和治疗模型但仍使用我们的低体重数据的情况。
结果模型将包括
- 母亲的年龄
- 孕早期产前检查的指标
- 母亲婚姻状况的指标
- ：第一胎的指标
治疗模式将包括
- 结果模型的所有协变量
- 母亲的年龄 ^ 2
- 方法：孕产妇教育年限
我们还将指定aequations选项，以报告结果和治疗模型的系数。
Iteration 0: EE criterion = 1.001e-20
Iteration 1: EE criterion = 1.134e-25
Treatment-effects estimation Number of obs = 4642
Estimator : IPW regression adjustment
Outcome model : linear
Treatment model: probit
-------------------------------------------------------------------------------
| Robust
bweight | Coef. Std. Err. z P>|z| [95% Conf. Interval]
--------------+----------------------------------------------------------------
POmeans |
mbsmoke |
nonsmoker | 3403.336 9.57126 355.58 0.000 3384.576 3422.095
smoker | 3173.369 24.86997 127.60 0.000 3124.624 3222.113
--------------+----------------------------------------------------------------
OME0 |
mage | 2.893051 2.134788 1.36 0.175 -1.291056 7.077158
prenatal1 | 67.98549 28.78428 2.36 0.018 11.56933 124.4017
mmarried | 155.5893 26.46903 5.88 0.000 103.711 207.4677
fbaby | -71.9215 20.39317 -3.53 0.000 -111.8914 -31.95162
_cons | 3194.808 55.04911 58.04 0.000 3086.913 3302.702
--------------+----------------------------------------------------------------
OME1 |
mage | -5.068833 5.954425 -0.85 0.395 -16.73929 6.601626
prenatal1 | 34.76923 43.18534 0.81 0.421 -49.87248 119.4109
mmarried | 124.0941 40.29775 3.08 0.002 45.11193 203.0762
fbaby | 39.89692 56.82072 0.70 0.483 -71.46966 151.2635
_cons | 3175.551 153.8312 20.64 0.000 2874.047 3477.054
--------------+----------------------------------------------------------------
TME1 |
mmarried | -.6484821 .0554173 -11.70 0.000 -.757098 -.5398663
mage | .1744327 .0363718 4.80 0.000 .1031452 .2457202
|
c.mage#c.mage | -.0032559 .0006678 -4.88 0.000 -.0045647 -.0019471
|
fbaby | -.2175962 .0495604 -4.39 0.000 -.3147328 -.1204595
medu | -.0863631 .0100148 -8.62 0.000 -.1059917 -.0667345
_cons | -1.558255 .4639691 -3.36 0.001 -2.467618 -.6488926
-------------------------------------------------------------------------------输出的POmeans部分显示两个治疗组的POM。ATE现在计算为3173.369 – 3403.336 = -229.967。
OME0和OME1部分分别显示未处理组和已处理组的RA系数。
输出的TME1部分显示概率处理模型的系数。
与前两种情况一样，如果我们希望ATE出现标准错误等，我们将指定ate选项。如果我们需要ATET，则可以指定atet选项。
AIPW：增强型IPW估算器
IPWRA估算器对结果和治疗方法进行建模，以说明非随机治疗方案。AIPW估算器也是如此。
AIPW估算器向IPW估算器添加偏差校正项。如果正确指定了处理模型，则偏差校正项为0，并且将模型简化为IPW估计量。如果治疗模型指定不正确，但结果模型指定正确，则偏差校正项会校正估计量。因此，偏差校正项使AIPW估计器具有与IPWRA估计器相同的双重鲁棒性。
AIPW估计器的语法和输出与IPWRA估计器的语法和输出几乎相同。
Iteration 0: EE criterion = 4.632e-21
Iteration 1: EE criterion = 5.810e-26
Treatment-effects estimation Number of obs = 4642
Estimator : augmented IPW
Outcome model : linear by ML
Treatment model: probit
-------------------------------------------------------------------------------
| Robust
bweight | Coef. Std. Err. z P>|z| [95% Conf. Interval]
--------------+----------------------------------------------------------------
POmeans |
mbsmoke |
nonsmoker | 3403.355 9.568472 355.68 0.000 3384.601 3422.109
smoker | 3172.366 24.42456 129.88 0.000 3124.495 3220.237
--------------+----------------------------------------------------------------
OME0 |
mage | 2.546828 2.084324 1.22 0.222 -1.538373 6.632028
prenatal1 | 64.40859 27.52699 2.34 0.019 10.45669 118.3605
mmarried | 160.9513 26.6162 6.05 0.000 108.7845 213.1181
fbaby | -71.3286 19.64701 -3.63 0.000 -109.836 -32.82117
_cons | 3202.746 54.01082 59.30 0.000 3096.886 3308.605
--------------+----------------------------------------------------------------
OME1 |
mage | -7.370881 4.21817 -1.75 0.081 -15.63834 .8965804
prenatal1 | 25.11133 40.37541 0.62 0.534 -54.02302 104.2457
mmarried | 133.6617 40.86443 3.27 0.001 53.5689 213.7545
fbaby | 41.43991 39.70712 1.04 0.297 -36.38461 119.2644
_cons | 3227.169 104.4059 30.91 0.000 3022.537 3431.801
--------------+----------------------------------------------------------------
TME1 |
mmarried | -.6484821 .0554173 -11.70 0.000 -.757098 -.5398663
mage | .1744327 .0363718 4.80 0.000 .1031452 .2457202
|
c.mage#c.mage | -.0032559 .0006678 -4.88 0.000 -.0045647 -.0019471
|
fbaby | -.2175962 .0495604 -4.39 0.000 -.3147328 -.1204595
medu | -.0863631 .0100148 -8.62 0.000 -.1059917 -.0667345
_cons | -1.558255 .4639691 -3.36 0.001 -2.467618 -.6488926
-------------------------------------------------------------------------------ATE为3172.366 – 3403.355 = -230.989。
最后的想法
上面的示例使用了一个连续的结果：出生体重。 teffects也可以用于二进制，计数和非负连续结果。
估计量还允许多个治疗类别。
参考文献：
【1】 Cattaneo, M. D. 2010. Efficient semiparametric estimation of multi-valued treatment effects under ignorability. Journal of Econometrics 155: 138–154.
【2】 stata博客