R语言Markowitz马克维茨投资组合理论分析和可视化

原文链接： http://tecdat.cn/?p=14200

之前我们在关于投资组合优化相关的内容中已经看到了Markowitz的理论，其中给出了预期收益和协方差矩阵

1.  
   > pzoo = zoo ( StockIndex , order.by = rownames ( StockIndex ) )
2.  
   > rzoo = ( pzoo / lag ( pzoo , k = -1) - 1 ) * 100
3.  
   >
4.  
    
5.  
   ans <- do.call ( method , list ( x = x , ... ) ) + return ( getCov ( ans ) )} > covmat=Moments(as.matrix(rzoo),"CovClassic")
6.  
   > (covmat=round(covmat,1))
7.  
   SP500 N225 FTSE100 CAC40 GDAX HSI
8.  
   SP500   17.8 12.7 13.8 17.8 19.5 18.9
9.  
   N225    12.7 36.6 10.8 15.0 16.2 16.7
10.  
    FTSE100 13.8 10.8 17.3 18.8 19.4 19.1
11.  
    CAC40   17.8 15.0 18.8 30.9 29.9 22.8
12.  
    GDAX    19.5 16.2 19.4 29.9 38.0 26.1
13.  
    HSI     18.9 16.7 19.1 22.8 26.1 58.1

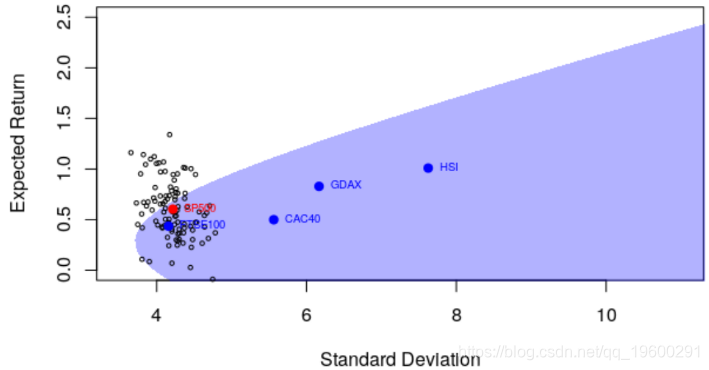
现在，我们可以可视化下面的有效边界（和可接受的投资组合）

1.  
    
2.  
    
3.  
    
4.  
    
5.  
    
6.  
   > points(sqrt(diag(covmat)),er,pch=19,col="blue")
7.  
   > text(sqrt(diag(covmat)),er,names(er),pos=4, col="blue",cex=.6)
8.  
   > polygon(u,v,border=NA,col=rgb(0,0,1,.3))

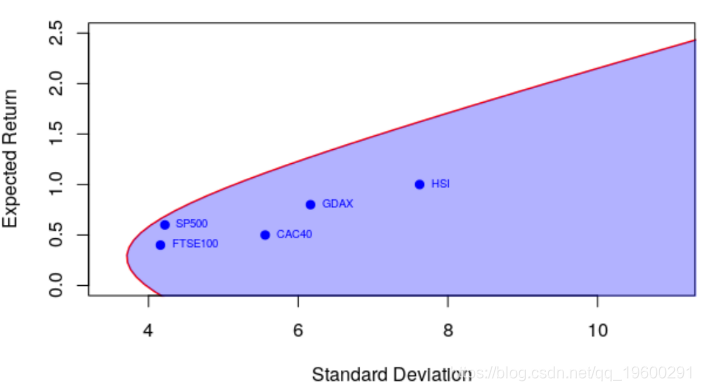
实际上很难在该图上将重要的东西可视化：收益之间的相关性。它不是点（单变量，具有预期收益和标准差），而是有效边界。例如，这是我们的相关矩阵

1.  
    
2.  
    
3.  
   SP500 N225 FTSE100 CAC40 GDAX HSI
4.  
   SP500   1.00 0.50 0.79 0.76 0.75 0.59
5.  
   N225    0.50 1.00 0.43 0.45 0.43 0.36
6.  
   FTSE100 0.79 0.43 1.00 0.81 0.76 0.60
7.  
   CAC40   0.76 0.45 0.81 1.00 0.87 0.54
8.  
   GDAX    0.75 0.43 0.76 0.87 1.00 0.56
9.  
   HSI     0.59 0.36 0.60 0.54 0.56 1.00

我们实际上可以更改FT500和FTSE100之间的相关性（此处为.786）

1.  
   courbe=function(r=.786){
2.  
    
3.  
   ef
4.  
   plot(ef$sd,ef$er,type="l",xlab="Standard Deviation",ylab="Expected Return",
5.  
   points(sqrt(diag(covmat)),er,pch=19,col=c("blue","red")[c(2,1,2,1,1,1)])
6.  
    
7.  
   polygon(u,v,border=NA,col=rgb(0,0,1,.3))
8.  
   }

例如，相关系数为0.6，我们得到以下有效边界

> courbe(.6)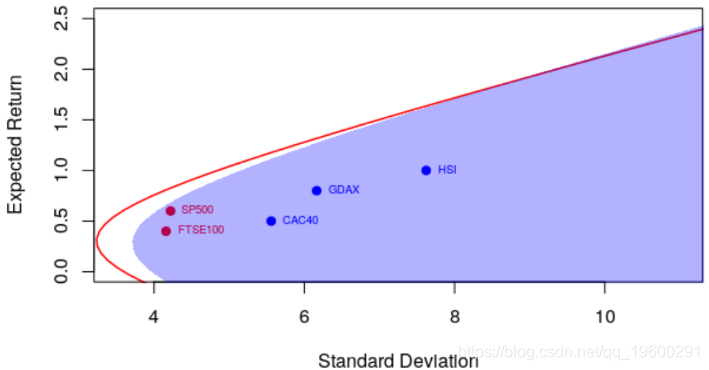

并具有更强的相关性

> courbe(.9)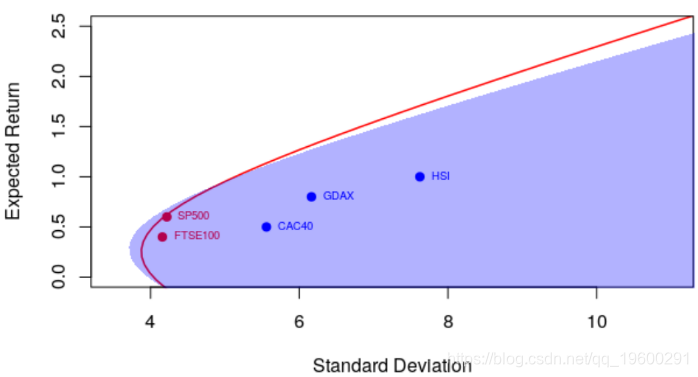

很明显，相关性很重要。但更重要的是，期望收益和协方差不是给出而是估计的。以前，我们确实将标准估计量用于方差矩阵。但是可以考虑使用另一个更可靠的估计器

1.  
   covmat=Moments(as.matrix(rzoo),"CovSde")
2.  
    
3.  
    
4.  
    
5.  
    
6.  
    
7.  
   points(sqrt(diag(covmat)),er,pch=19,col="blue")
8.  
   text(sqrt(diag(covmat)),er,names(er),pos=4,col="blue",cex=.6)
9.  
   polygon(u,v,border=NA,col=rgb(0,0,1,.3))

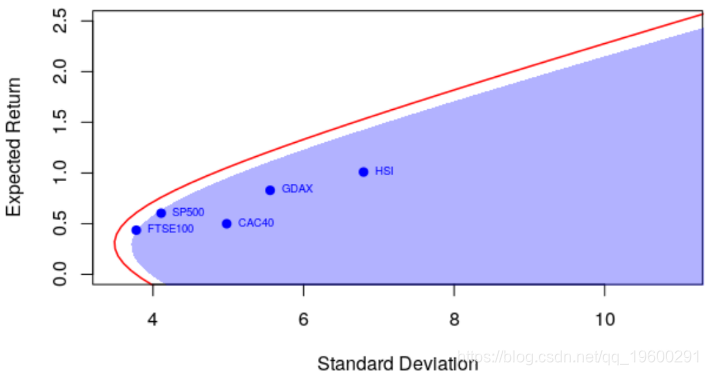
它确实影响了点的（水平）位置，因为方差现在以及有效边界都不同，而方差明显更低。

为了说明最后一点，说明我们确实有基于观察到的收益的估计量，如果我们观察到不同的收益怎么办？了解可能发生的情况的一种方法是使用引导程序，例如每日收益。

1.  
    
2.  
    
3.  
    
4.  
    
5.  
    
6.  
    
7.  
   > plot(ef$sd,ef$er,type="l",xlab="Standard Deviation",ylab="Expected Return", xlim=c(3.5,11),ylim=c(0,2.5),col="white",lwd=1.5)
8.  
   > polygon(u,v,border=NA,col=rgb(0,0,1,.3))
9.  
   > for(i in 1:100){
10.  
    +
11.  
    +
12.  
    + er=apply(as.matrix(rzoo)[id,],2,mean)
13.  
    + points(sqrt(diag(covmat))[k],er[k],cex=.5)
14.  
    + }

或其他资产

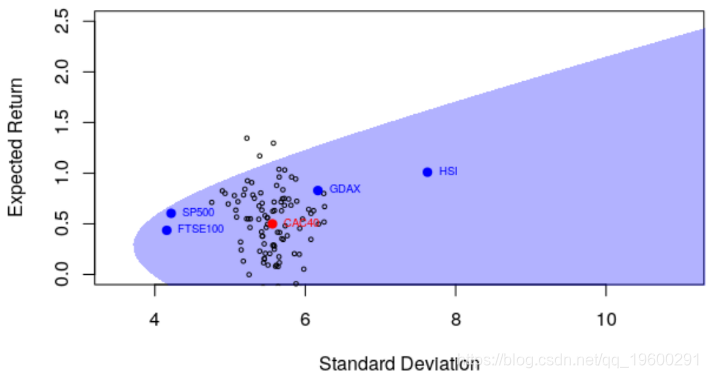
这是我们在（估计的）有效边界上得到的

1.  
    
2.  
    
3.  
    
4.  
    
5.  
    
6.  
    
7.  
    
8.  
   > polygon(u,v,border=NA,col=rgb(0,0,1,.3))
9.  
   > for(i in 1:100){
10.  
    +
11.  
    +
12.  
    +
13.  
    + ef <- efficient.frontier(er, covmat, alpha.min=-2.5, alpha.max=2.5, nport=50)
14.  
    + lines(ef$sd,ef$er,col="red")
15.  
    + }

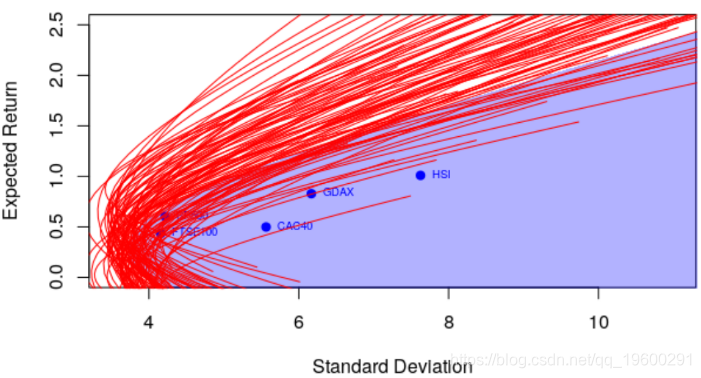
因此，至少在统计学的角度上，要评估一个投资组合是否最优是很困难的。

---

参考文献

1.用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)的应用

2.R语言GARCH-DCC模型和DCC（MVT）建模估计

3.R语言实现 Copula 算法建模依赖性案例分析报告

4.R语言使用ARIMA模型预测股票收益

5.r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

6.用R语言实现神经网络预测股票实例

7.r语言预测波动率的实现：ARCH模型与HAR-RV模型

8.R语言如何做马尔科夫转换模型markov switching model