拓端tecdat|R语言Lee-Carter模型对年死亡率建模预测预期寿命

原文链接：http://tecdat.cn/?p=17347

昨天上午，我们获得了分娩产妇的平均年龄两个图表，根据孩子的出生顺序排序，区间是1905-1965年：

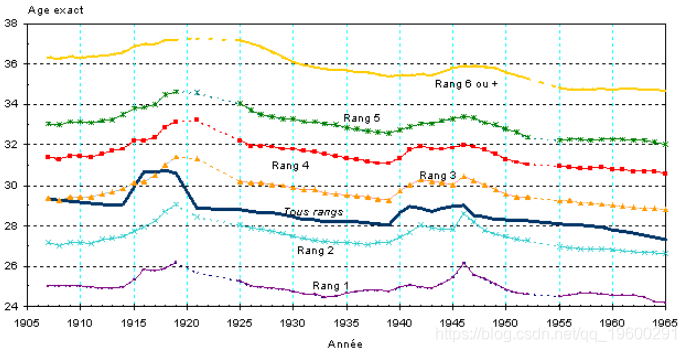
然后是1960-2000年：

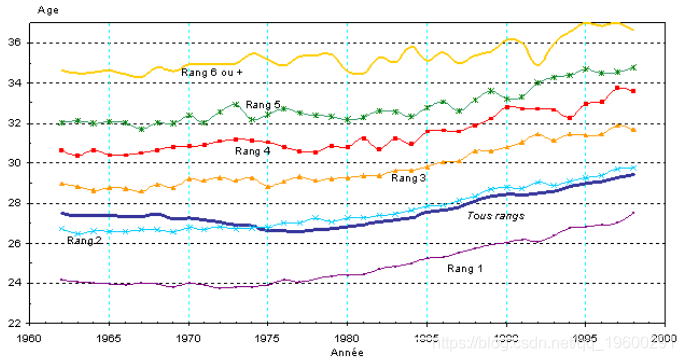
这些图形令人兴奋，特别是在过去30年中观察到的增长方面，这使我想到了寿命的增长趋势。我们可以找到其他有趣的数据（在这种情况下为平均 出生年龄 ）。

1.  
    
2.  
   > age$Age=as.character(age$AGE)
3.  
   > age$AGE=as.numeric(substr(age$Age,1,2))+
4.  
   + as.numeric(substr(age$Age,4,4))/10
5.  
   > plot(age$ANNEE+.5,age$AGE,
6.  
   + type="l",lwd=2,col="blue")

我们在上面的图中发现深蓝色的曲线，

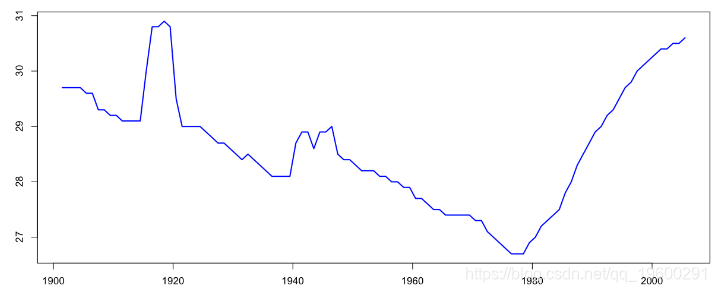
获取祖母的平均年龄，我们进一步分析

1.  
    
2.  
   > tail(age)
3.  
   AGE Age NAIS.MERE NAIS.GRD.MERE age.GRD.MERE
4.  
   2000 2000 30.3 30,3 1970.2 1942.87 57.63
5.  
   2001 2001 30.4 30,4 1971.1 1943.80 57.70
6.  
   2002 2002 30.4 30,4 1972.1 1944.92 57.58
7.  
   2003 2003 30.5 30,5 1973.0 1945.95 57.55
8.  
   2004 2004 30.5 30,5 1974.0 1947.05 57.45
9.  
   2005 2005 30.6 30,6 1974.9 1948.04 57.46
10.  
    > plot(age$ANNEE+.5,age$age.GRD.MERE,
11.  
    + type="l",lwd=2,col="red")

再一次，我们可以形象地看到外婆的出生年龄

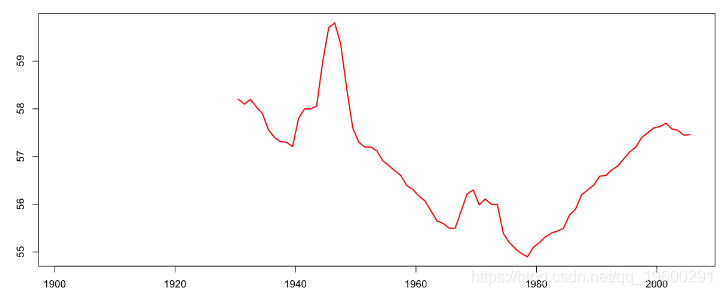
我们可以通过使用Lee-Carter模型对年死亡率进行建模，并推断到当前世纪，我们可以推断出剩余预期寿命。

1.  
   > Deces <- read.table("Dec.txt",header=TRUE)
2.  
   > Expo <- read.table("Expo.txt",header=TRUE,skip=2)
3.  
   > Deces$Age <- as.nu
4.  
   > Expo$Age <- as.numeric(as.character(Expo$Age))
5.  
   > Expo$Age[is.n
6.  
   Deces$Female/Expo$Female,nL,nC)
7.  
   > POPF <- matrix(Expo$Female,nL,nC)
8.  
   > BASEF <- demogdata(data=MUF, pop=POPF,ages=AGE,
9.  
   + years=YEAR, t
10.  
    > K1 <- LCF$kt
11.  
    nction(xentier,T){
12.  
     
13.  
    + return(ext) }
14.  
    > EVIE = function(x,T){
15.  
    + x1 <- trunc(x)
16.  
    > tail(age)
17.  
    AGE Age NAIS.MERE NAIS.GRD.MERE age.GRD.MERE EV
18.  
    2000 30.3 30,3 1970.2 1942.87 57.63 29.13876
19.  
    2001 30.4 30,4 1971.1 1943.80 57.70 29.17047
20.  
    2002 30.4 30,4 1972.1 1944.92 57.58 29.39027
21.  
    2003 30.5 30,5 1973.0 1945.95 57.55 29.52041
22.  
    2004 30.5 30,5 1974.0 1947.05 57.45 29.72511
23.  
    2005 30.6 30,6 1974.9 1948.04 57.46 29.80398

换句话说，在最后一行，2005年，一名57.46岁女性的（剩余）预期寿命约为29.80岁。然后，我们不仅可以看到他祖母的平均年龄，还可以看到她的剩余预期寿命，

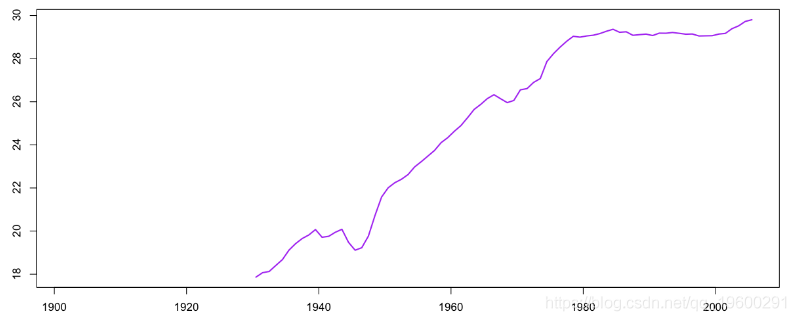
然后我们就可以确定曾祖母的（平均）年龄，

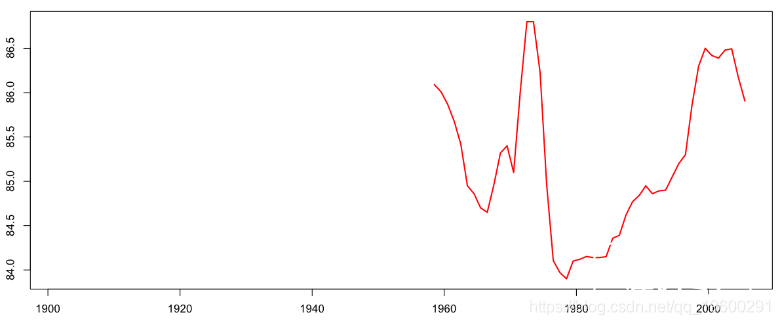
以及曾祖母的（剩余）寿命

现在我们也可以对这项快速研究的局限性感到疑惑。特别是，正如有配偶的寿命之间存在很强的相关性，我们可能会问，孩子和孙子的出生是否具有对一个人的剩余生命的影响（或者我们是否可以像这样假设独立性）。

---

专栏

精算科学

关于结合数学、统计方法以及程序语言对经济活动来做风险分析、评估的见解。

探索专栏 ➔