拓端tecdat|R语言最大流最小割定理和最短路径算法分析交通网络流量拥堵问题

 原文链接：http://tecdat.cn/?p=17635 

今天早上，我们使用一些论文中提到的示例，使用最大流最小割定理将流量拥塞降至最低， 并应用了最短路径分析了交通瓶颈。

我们可以在下面看到

1.  
    
2.  
   map=openp(map)
3.  
   plot(map)
4.  
   points(t(m[3:2,]),col="black", pch=19, cex=3

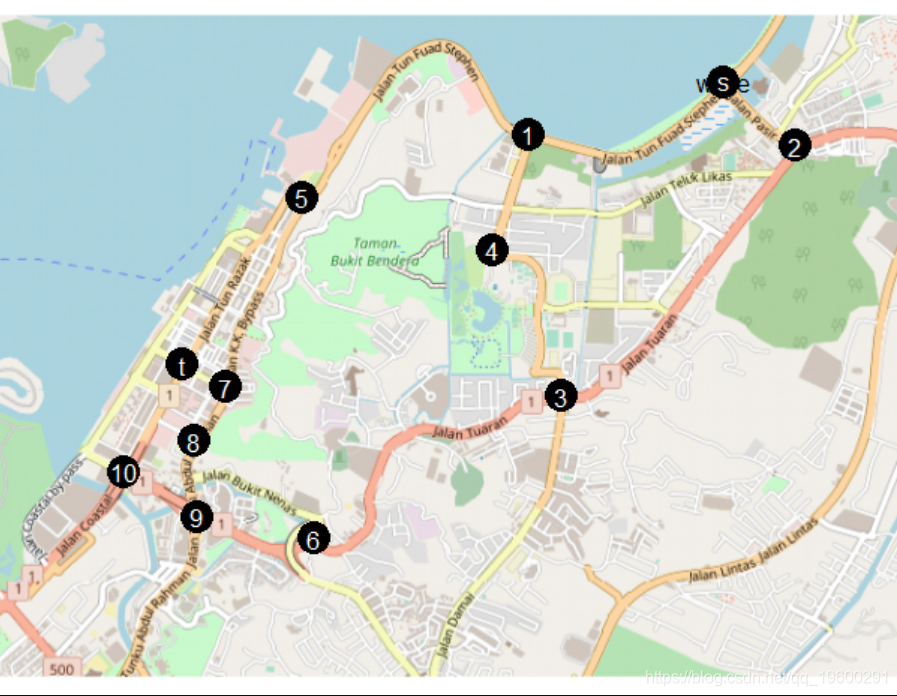
要提取有关边缘容量的信息，在该网络上使用以下代码，该代码将从论文中提取三个表

1.  
    
2.  
   extract_tab(location)

在Windows中，要先下载另一个软件包

1.  
   library(devtools)
2.  
    
3.  
   extract_tab(locatio

现在我们可以得出具有容量的数据框

1.  
   B1=as.data.frame(out[[2]])
2.  
   B2=as.data.frame(out[[3
3.  
    
4.  
   capacity=as.character(B2$V3[-1])
5.  
   capacity[6]="843"
6.  
   ic(capacity)

我们可以在地图上添加这些边

1.  
   plot(map)
2.  
   points(t(m[3:2,]),col="black", pch=1
3.  
    
4.  
   for(i in 1:nrow(E)){
5.  
   i1=which(B$i==as.character(E$from
6.  
   ]))
7.  
   segments(B[i1,"x"],B[i1,"y"],B[i2,
8.  
    
9.  
   text(t(m[3:2,]),c("s",1:10,"t"),col="white")

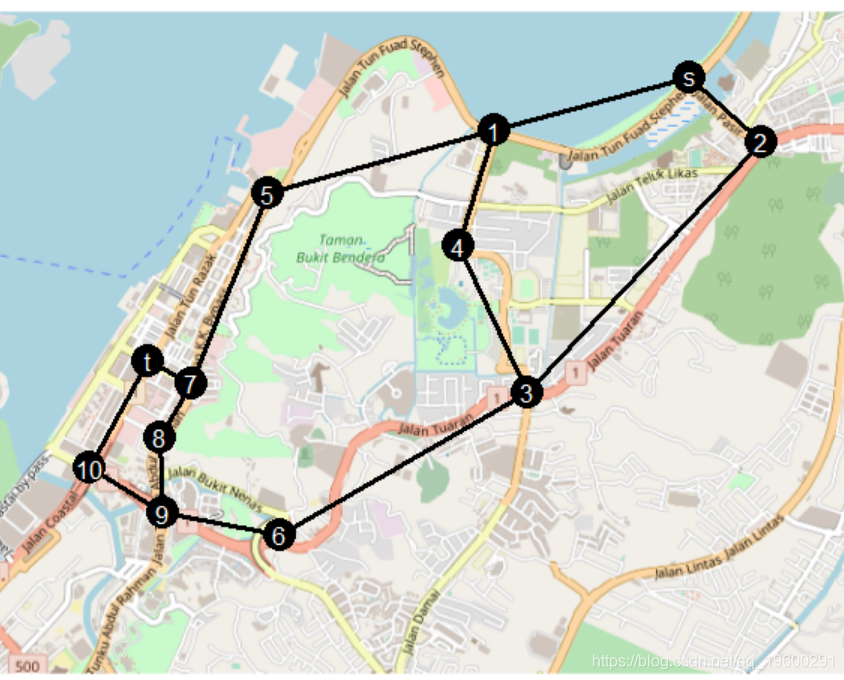
要获得具有容量的图形，可以使用另一种方法

1.  
   g=graph_from_data_frame(E)
2.  
   E(g)$label=E$capacity
3.  
   plot(g)

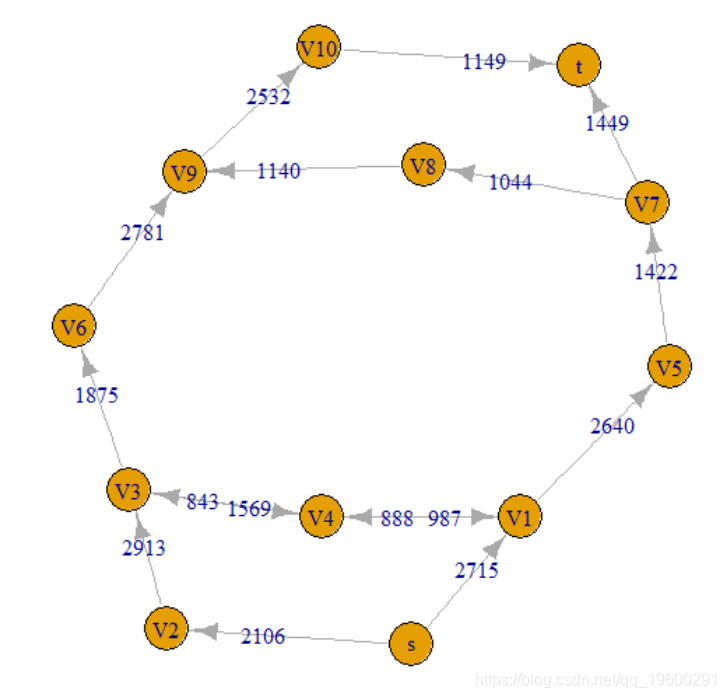
但是它不考虑节点的地理位置。可以使用

1.  
   plot(g, layout=as.matrix(B[,c("x","y")]))
2.  
    

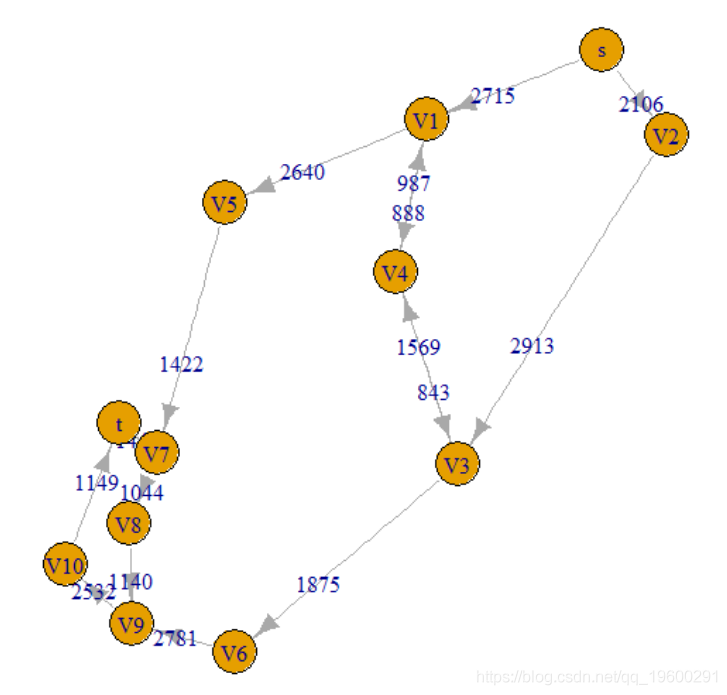
为了更好地了解道路通行能力，使用

1.  
   plot(g, layout=as.matrix(B[,c("x","y")]),
2.  
   edge.width=E$capacity/200)

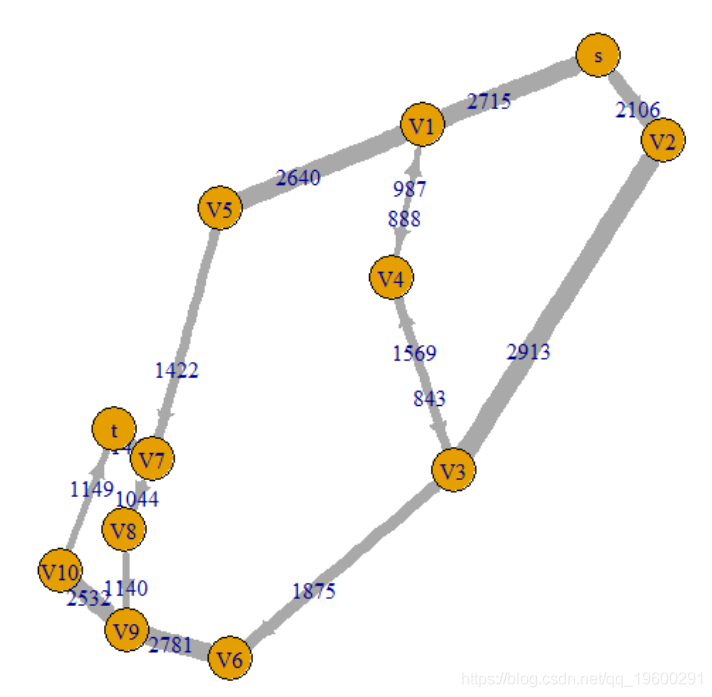
通过具有容量的网络，目标是确定该网络上从源到宿的最大流量。可以使用R

1.  
   $value
2.  
   [1] 2571
3.  
    
4.  
   $flow
5.  
   [1] 10 142 130 23 0 2

我们的最大流量为2571，这与两篇论文中的最大流量最小割定理以及 最短路径的应用中都实际要求的不同   ，因为表格和图表上的值不同。

1.  
   E$flux1=m$flow
2.  
   plot(g, layout=as.matrix(B[,c("x","y")]),

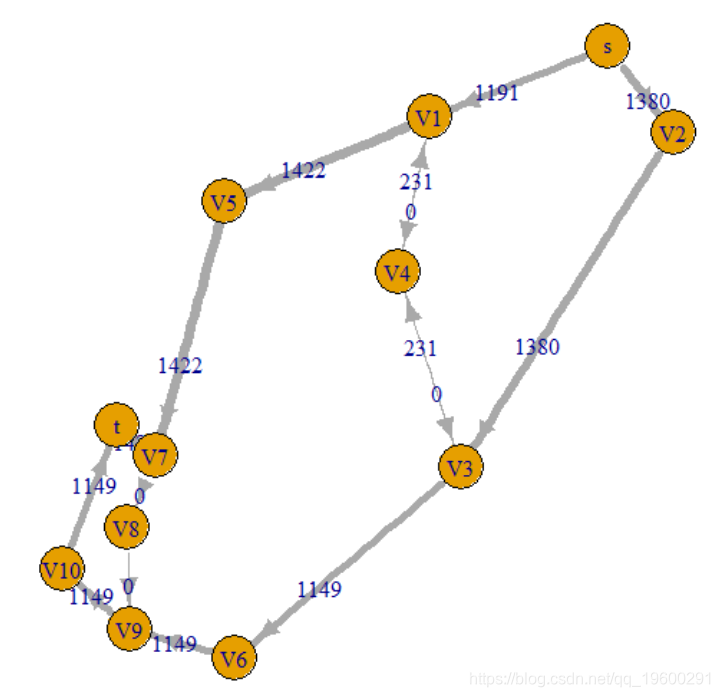
考虑采用更简单的流程，但是相同的全局值

1.  
    
2.  
    
3.  
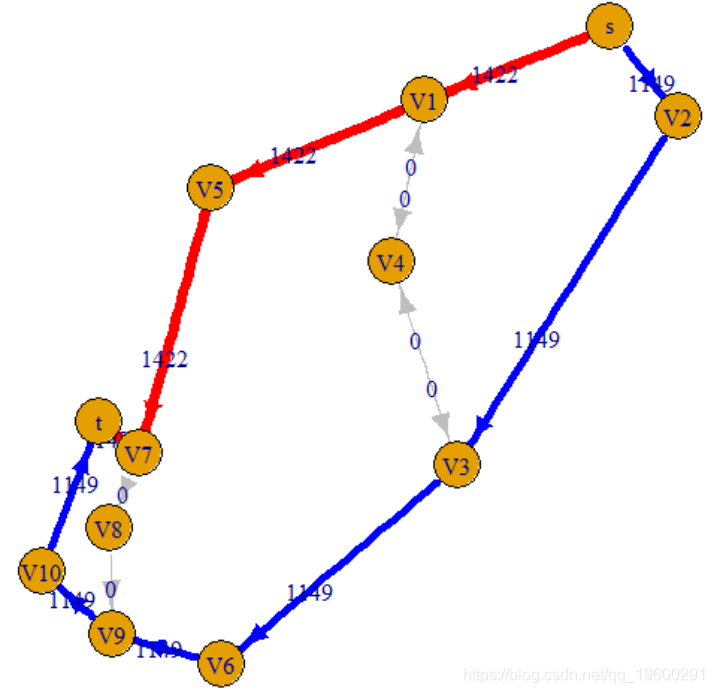
   E(g)$label=E$flux2
4.  
   plot(g, layout=as.matrix(B[,c("x","y")]),
5.  
   edge.width=E$flux2/200)

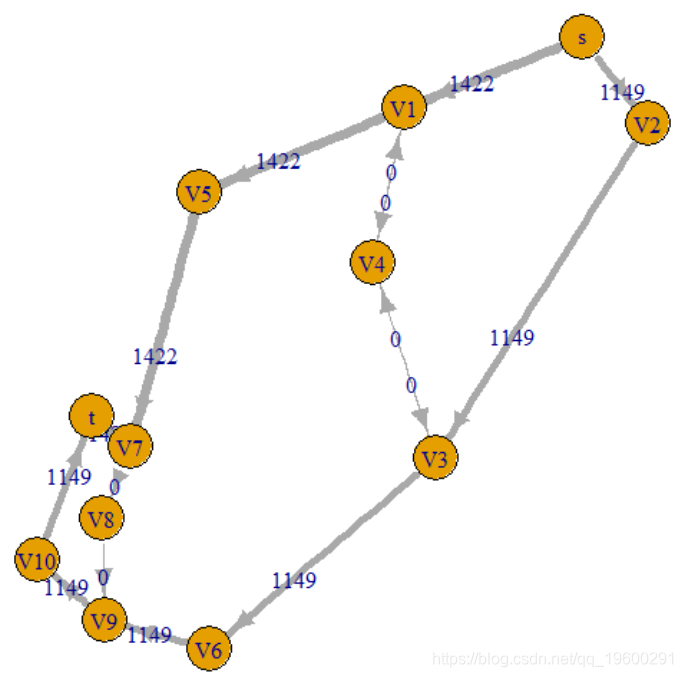
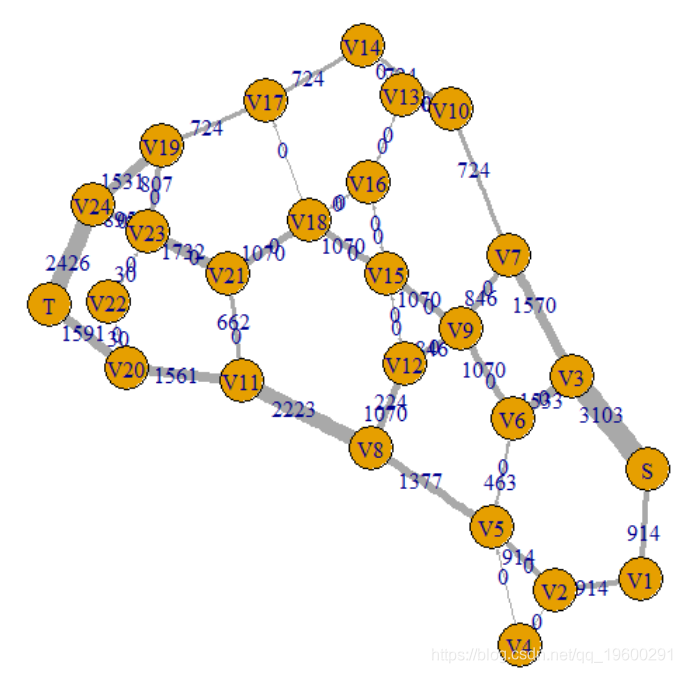
实际上，有可能在同一城市的另一篇论文中做同样的事情，这是道路网络的交通拥堵问题。

1.  
    
2.  
    
3.  
   dim(out[[3]])
4.  
   B1=a
5.  
   ame(from=B1[2:61,"V2"],
6.  
   to=B1[2:6
7.  
   as.numeric(
8.  
   as.characte
9.  
   data_frame(E)
10.  
    m=max_flow(graph=g,
11.  
    source="S",
12.  
     
13.  
    E$flux1=m$flow
14.  
    E(g)$label=E
15.  
     
16.  
    edge.width=E$flux1/200,
17.  
    edge.arrow.size=0.15)

此处的最大流量值为4017，就像原始论文中发现的那样

---

最受欢迎的见解 

1.R语言动态图可视化：如何、创建具有精美动画的图

2.TABLEAU的骑行路线地理数据可视化

3.用数据告诉你出租车资源配置是否合理

4.R语言GGMAP空间可视化机动车交通事故地图

5.用R语言制作交互式图表和地图

6.基于出租车GPS轨迹数据的研究：出租车行程的数据分析

7.R语言动态可视化：制作历史全球平均温度的累积动态折线图动画gif视频图

8.把握出租车的数据脉搏

9.共享单车大数据报告