R语言动量和马科维茨Markowitz投资组合(Portfolio)模型实现

原文链接：http://tecdat.cn/?p=17931 

动量和马科维茨投资组合模型使 均值方差优化 组合成为可行的解决方案。通过建议并测试：

• 增加最大权重限制
• 增加目标波动率约束

来控制 均值方差最优化的解。

下面，我将查看8个资产的结果：

首先，让我们加载所有历史数据

1.  
   #*****************************************************************
2.  
   # 加载历史数据
3.  
    
4.  
   #*****************************************************************
5.  
    
6.  
   load.packages('quantmod')
7.  
    
8.  
   # 加载保存的原始数据
9.  
   #
10.  
    load('raw.Rdata')
11.  
     
12.  
     
13.  
     
14.  
    getSymbols.extra(N8.tickers, src = 'yahoo', from = '1970-01-01', env = data, raw.data =
15.  
    for(i in data$symbolnames) data[[i]] = adjustOHLC(data[[i]]
16.  
     

接下来，让我们测试函数

1.  
   #*****************************************************************
2.  
   # 运行测试，每月数据
3.  
   #*****************************************************************
4.  
    
5.  
   plot(scale.one(data$prices))

1.  
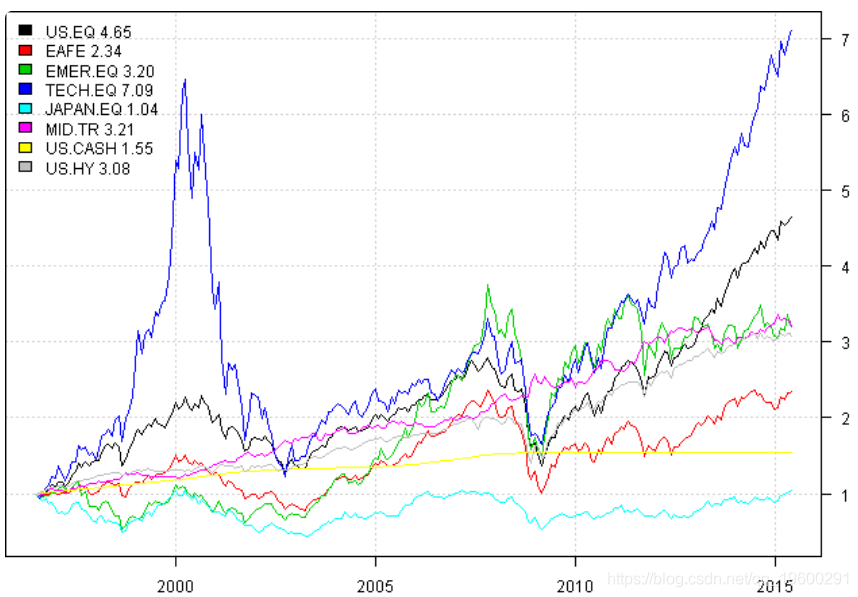
   prices = data$prices
2.  
    
3.  
   plotransition(res[[1]]['2013::'])

 

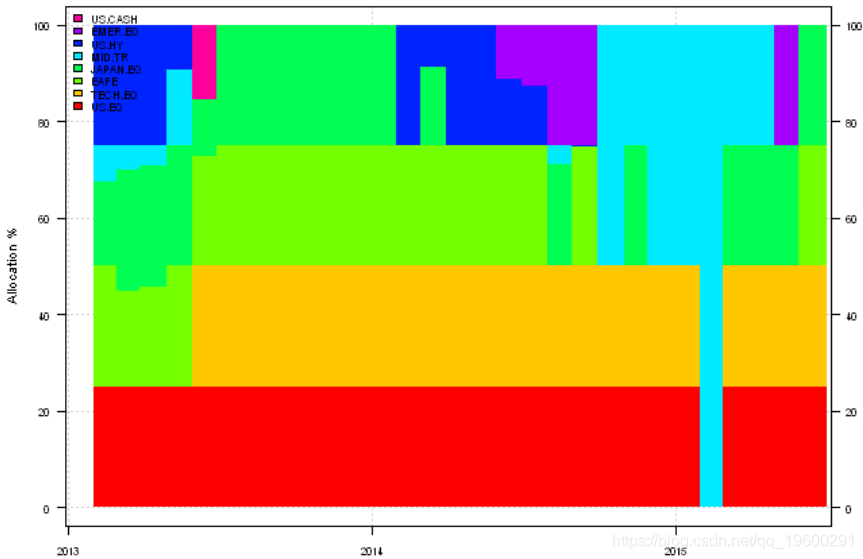
接下来，让我们创建一个基准并设置用于所有测试。

1.  
   #*****************************************************************
2.  
   # 建立基准
3.  
   #*****************************************************************
4.  
   models = list()
5.  
    
6.  
   commission = list(cps = 0.01, fixed = 10.0, percentage = 0.0)
7.  
    
8.  
   data$weight[] = NA
9.  
    
10.  
    model = brun(data, clean.signal=T,

接下来，让我们获取权重，并使用它们来进行回测

1.  
   #*****************************************************************
2.  
   # 转换为模型结果
3.  
   #*****************************************************************
4.  
   CLA = list(weight = res[[1]], ret = res[[2]], equity = cumprod(1 + res[[2]]), type = "weight")
5.  
    
6.  
   obj = list(weights = list(CLA = res[[1]]), period.ends

我们可以复制相同的结果

1.  
   #*****************************************************************
2.  
   #进行复制
3.  
   #*****************************************************************
4.  
   weight.limit = data.frame(last(pric
5.  
   obj = portfoli(data$prices,
6.  
   periodicity = 'months', lookback.len = 12, silent=T,
7.  
   const.ub = weight.limit,urns,1) + colSums(last(hist.returns,3)) +
8.  
   colSums(last(hist.returns,6)) + colSums(last(hist.returns,12))) / 22
9.  
   ia
10.  
    },
11.  
    min.risk.fns = list(
12.  
    )
13.  
     
14.  
     

另一个想法是使用Pierre Chretien的平均输入假设

1.  
   #*****************************************************************
2.  
   # 让我们使用Pierre的平均输入假设
3.  
   #*****************************************************************
4.  
   obj = portfolio(data$prices,
5.  
   periodicity = 'months', lookback.len = 12, si
6.  
   create.ia.fn = create.(c(1,3,6,12), 0),
7.  
   min.risk.fns = list(
8.  
   TRISK.AVG = target.risk.portfolio(target.r
9.  
   )
10.  
     

最后，我们准备看一下结果

1.  
   #*****************************************************************
2.  
   #进行回测
3.  
   #*****************************************************************
4.  
    
5.  
   plotb(models, plotX = T, log = 'y', Left

1.  
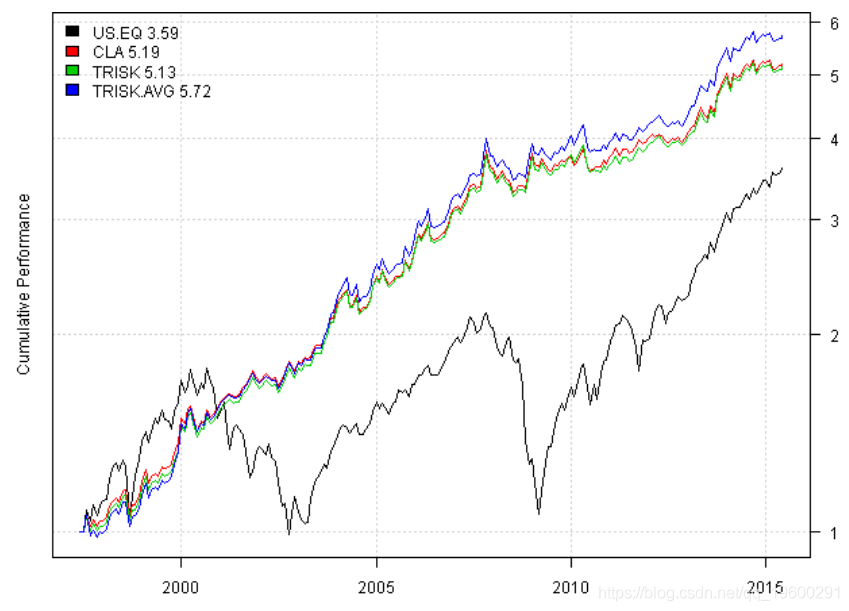
   layout(1)
2.  
   barplot(sapply(models, turnover, data)

使用平均输入假设会产生更好的结果。

我想应该注意的主要观点是：避免盲目使用优化。相反，您应该使解决方案更具有稳健性。

---

最受欢迎的见解

1.用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)的应用

2.R语言GARCH-DCC模型和DCC（MVT）建模估计

3.R语言实现 Copula 算法建模依赖性案例分析报告

4.R语言COPULAS和金融时间序列数据VaR分析

5.R语言多元COPULA GARCH 模型时间序列预测

6.用R语言实现神经网络预测股票实例

7.r语言预测波动率的实现：ARCH模型与HAR-RV模型

8.R语言如何做马尔科夫转换模型markov switching model

9.matlab使用Copula仿真优化市场风险