拓端数据tecdat|R语言ARIMA，SARIMA预测道路交通流量时间序列:季节性、周期性

原文链接：http://tecdat.cn/?p=20434

本文从实践角度讨论了季节性单位根。我们考虑一些时间序列 ，例如道路上的交通流量，

1.  
    
2.  
   > plot(T,X,type="l")
3.  
   > reg=lm(X~T)
4.  
   > abline(reg,col="red")

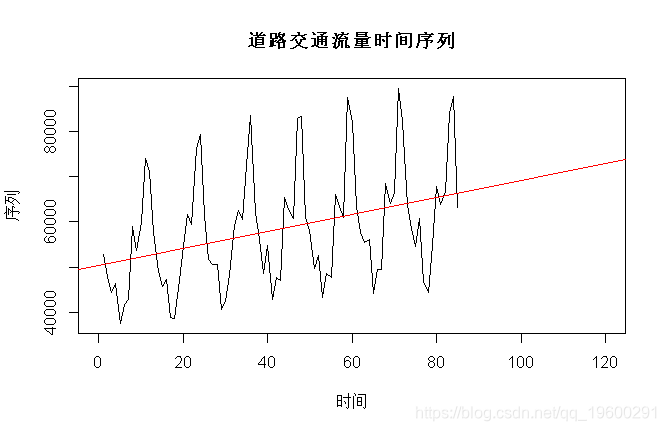
如果存在趋势，我们应该将其删除，然后处理残差 

1.  
   > Y=residuals(reg)
2.  
   > acf(Y,lag=36,lwd=3)

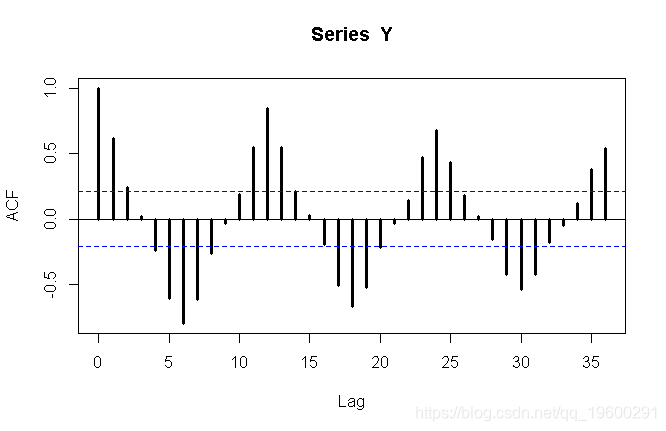
我们可以看到这里有一些季节性。第一个策略可能是假设存在季节性单位根，因此我们考虑 ，我们尝试找到ARMA模型。考虑时间序列的自相关函数，

1.  
   > Z=diff(Y,12)
2.  
   > acf(Z,lag=36,lwd=3)

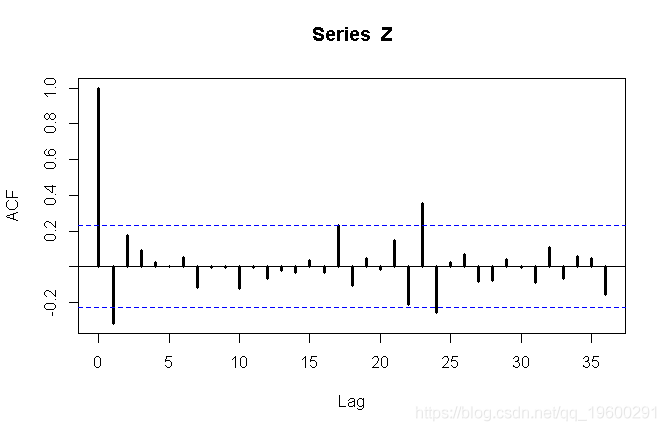
或偏自相关函数

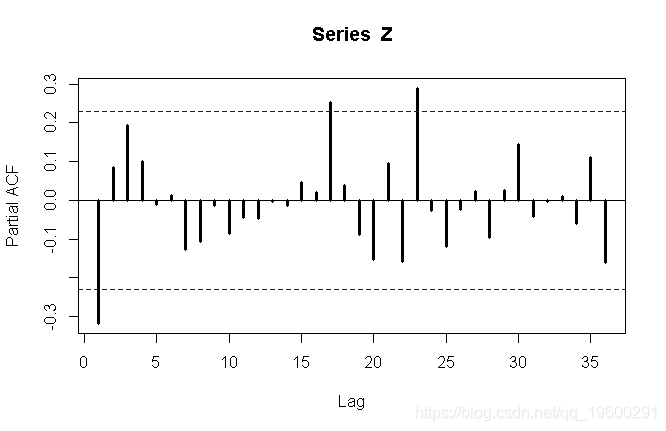
第一个图可能建议MA（1），而第二个图可能建议AR（1）时间序列。我们都尝试。

1.  
    
2.  
   arima
3.  
   Coefficients:
4.  
   ma1 intercept
5.  
   -0.2367 -583.7761
6.  
   s.e. 0.0916 254.8805
7.  
    
8.  
   sigma^2 estimated as 8071255: log likelihood = -684.1, aic = 1374.2

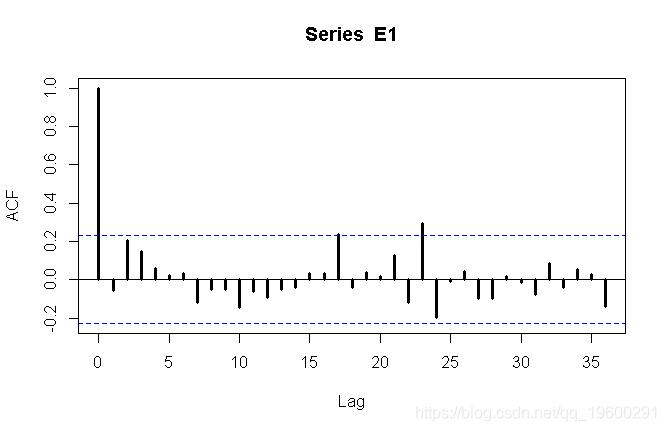
可以认为是白噪声（如果您不确定，请尝试 Box-Pierce或Ljung-Box 测试）。

1.  
    
2.  
   arima
3.  
   Coefficients:
4.  
   ar1 intercept
5.  
   -0.3214 -583.0943
6.  
   s.e. 0.1112 248.8735
7.  
    
8.  
   sigma^2 estimated as 7842043: log likelihood = -683.07, aic = 1372.15

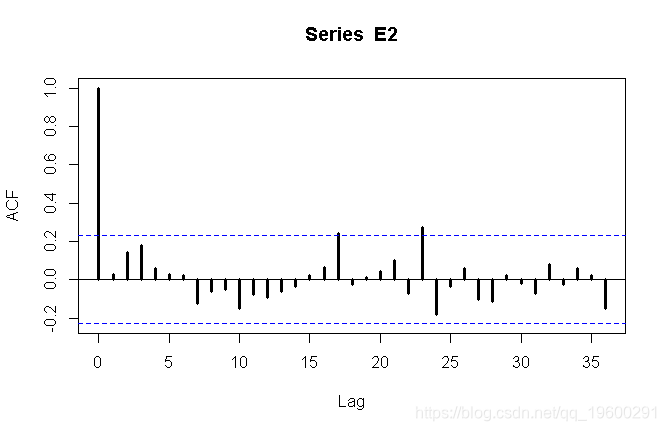
也可以视为白噪声。到目前为止，我们有

对于一些白噪声 。这表明以下的SARIMA结构 ，

1.  
    
2.  
   arima
3.  
   Coefficients:
4.  
   ar1
5.  
   -0.2715
6.  
   s.e. 0.1130
7.  
    
8.  
   sigma^2 estimated as 8412999: log likelihood = -685.62, aic = 1375.25

现在，如果我们认为我们没有季节性单位根，而在AR结构中只是一个大的自回归系数。让我们尝试类似

自然而然的猜测是该系数应该（可能）接近于1。让我们尝试一下

1.  
    
2.  
   arima
3.  
   Coefficients:
4.  
   ar1 sar1 intercept
5.  
   -0.1629 0.9741 -684.9455
6.  
   s.e. 0.1170 0.0115 3064.4040
7.  
    
8.  
   sigma^2 estimated as 8406080: log likelihood = -816.11, aic = 1640.21

这与我们先前（以某种方式）获得的结果具有可比性，因此我们可以假设该模型是一个有趣的模型。我们将进一步讨论：第一个系数可能是不重要的。

这两个模型有什么区别？

从（非常）长期的角度来看，模型是完全不同的：一个模型是平稳的，因此预测将趋向于平均值，而另一个模型则是按季节的，因此置信区间将增加。我们得到

> pre(model2,600,b=60000)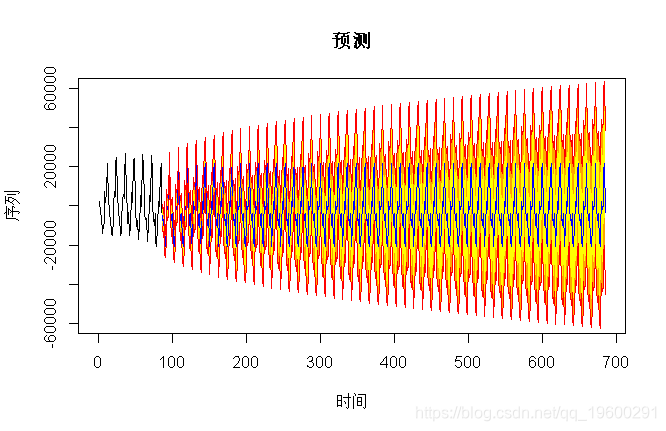

对于平稳的

> prev(model3,600,b=60000)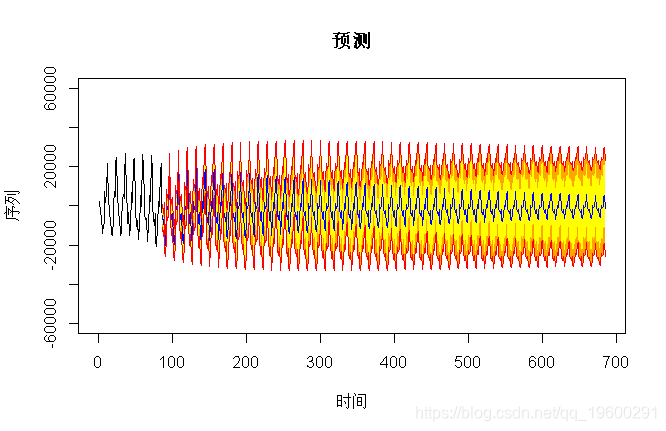

但是，使用这些模型进行的预测仅适用于短期范围。在这种情况下，这里的预测几乎相同，

> pre(model2,36,b=60000)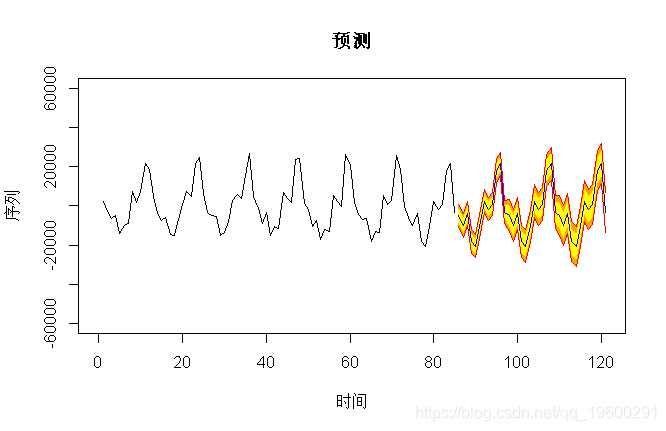

> pre(model3,36,b=60000)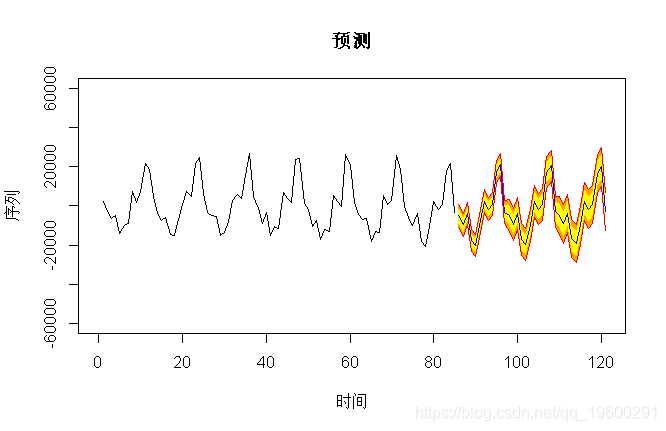

现在，如果我们回到第二个模型，自回归系数可能被认为是不重要的。如果我们将其删除怎么样？

1.  
    
2.  
   Call:
3.  
   seasonal = list(order = c(1, 0, 0)
4.  
   Coefficients:
5.  
   sar1 intercept
6.  
   0.9662 -696.5661
7.  
   s.e. 0.0134 3182.3017
8.  
    
9.  
   sigma^2 estimated as 8918630: log likelihood = -817.03, aic = 1640.07

如果我们看一下（短期）预测，我们得到

> pre(model,36,b=32000)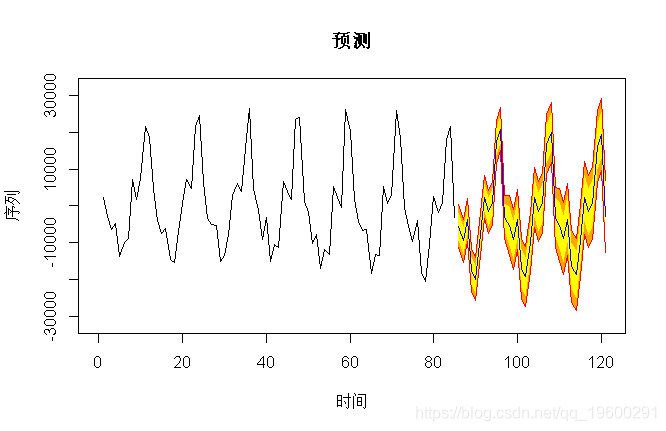

有什么区别吗？如果我们看一下预测结果数字，我们会得到

数字不同，但差异不大（请注意置信区间的大小）。这可以解释为什么在R中，当我们在自回归过程时 ，得到一个模型要估计的参数，即使其中不重要，我们通常也会保留它们来预测。

---

最受欢迎的见解

1.用于NLP的Python：使用Keras的多标签文本LSTM神经网络分类

2.Python中利用长短期记忆模型LSTM进行时间序列预测分析 – 预测电力消耗数据

3.python在Keras中使用LSTM解决序列问题

4.Python中用PyTorch机器学习分类预测银行客户流失模型

5.R语言多元Copula GARCH 模型时间序列预测

6.在r语言中使用GAM（广义相加模型）进行电力负荷时间序列分析

7.R语言中ARMA，ARIMA（Box-Jenkins），SARIMA和ARIMAX模型用于预测时间序列数

8.R语言估计时变VAR模型时间序列的实证研究分析案例

9.用广义加性模型GAM进行时间序列分析