原文链接:http://tecdat.cn/?p=20953
序言
本文演示了在时间序列分析中应用分布滞后线性和非线性模型(DLMs和DLNMs)。Gasparrini等人[2010]和Gasparrini[2011]阐述了DLMs和DLNMs的发展以及时间序列数据的实现。本文描述的示例涵盖了时间序列数据DLNM方法的大多数标准应用,并探讨了DLNM包用于指定、总结和绘制此类模型。尽管这些例子在空气污染和温度对健康的影响方面有具体的应用,但它们很容易被推广到不同的主题,并为分析这些数据集或其他时间序列数据源奠定了基础。
数据
示例使用时间序列数据集(包括1987-2000年期间每日观测数据)探索了空气污染和温度与死亡率之间的关系。在R会话中加载后,让我们看一下前三个观察结果:
-
-
date time year month doy dow death cvd resp temp dptp
-
1 1987-01-01 1 1987 1 1 Thursday 130 65 13 -0.2777778 31.500
-
2 1987-01-02 2 1987 1 2 Friday 150 73 14 0.5555556 29.875
-
3 1987-01-03 3 1987 1 3 Saturday 101 43 11 0.5555556 27.375
-
rhum pm10 o3
-
1 95.50 26.95607 4.376079
-
2 88.25 NA 4.929803
-
3 89.50 32.83869 3.751079
数据集由1987-2000年期间每天进行观测的序列组成。
示例1:一个简单的DLM
在第一个例子中,我指定了一个简单的DLM,评估PM10对死亡率的影响,同时调整温度的影响。我首先为这两个预测值建立两个交叉基矩阵,然后将它们包含在回归函数的模型公式中。假设PM10的影响在预测因子的维度上是线性的,因此,从这个角度来看,我们可以将其定义为一个简单的DLM,即使回归模型也估计了温度的分布滞后函数,这是一个非线性项。首先,我运行crossbasis()来构建两个交叉基矩阵,将它们保存在两个对象中。两个对象的名称必须不同,以便分别预测它们之间的关联。代码如下:
-
cb(pm10, lag=15, argvar=list(fun="lin",
-
arglag=list(fun="poly",degree=4
在具有时间序列数据的程序中,第一个参数x用于指定向量序列。在这种情况下,我们假设PM10的影响是线性的(fun=“lin”),同时通过一个具有5个自由度的自然三次样条曲线(fun=“ns”,默认选择)来模拟与温度的关系。内部结点(如果未提供)由ns()放置在默认的等距分位数处,而边界节点位于温度范围处。关于滞后空间的基数,我用4次多项式函数(设置次数=4)指定PM10长达15天的滞后效应(最小滞后默认为0)。温度的滞后效应由两个滞后层(0和1-3)定义,假设每个层内的效应为常数。参数breaks=1定义了第二个区间的下边界。此类的方法函数summary()提供了交叉基(以及二维中的相关基)的概述:
-
-
CROSSBASIS FUNCTIONS
-
observations: 5114
-
range: -3.049835 to 356.1768
-
lag period: 0 15
-
total df: 5
-
BASIS FOR VAR:
-
fun: lin
-
intercept: FALSE
-
BASIS FOR LAG:
-
fun: poly
-
degree: 4
-
scale: 15
-
intercept: TRUE
现在,在回归模型的模型公式中可以包含这两个交叉基对象。在这种情况下,我拟合时间序列模型,假设泊松分布,时间的光滑函数,7 df/年(为了校正季节性和长时间趋势)和星期几作为因子:
-
glm(death ~ cb1.pm + cb1.temp + ns(time, 7*14) + dow,
-
family=quasipoisson()
通过上述模型预测的PM10与死亡率的特定水平的估计关联可通过函数crosspred()进行总结,并保存在具有相同类的对象中:
pred(cb1.pm, model1, at=0:20, bylag=0.2, cumul=TRUE)
该函数包括用来估计参数的base1.pm和model1对象作为前两个参数,而at = 0:20表示必须为从0到20 µgr / m3的每个整数值计算预测。通过设置by lag = 0.2,沿着滞后空间以0.2的增量计算预测。绘制结果时,此更精细的网格产生更平滑的滞后曲线。参数cumul(默认为FALSE)指示还必须包括沿滞后的增量累积关联。没有通过参数cen定义中心,因此默认情况下将参考值设置为0(这种情况发生在函数lin()上)。现在,这些预测已存储在pred1.pm中,可以通过特定的方法对其进行绘制。例如:
-
> plot(pred1, "slices",
-
main="与PM10增加10个单位的关联性")
-
> plot(pred1,ylab="累计RR",
-
main="PM10增加10个单位的累积关联")
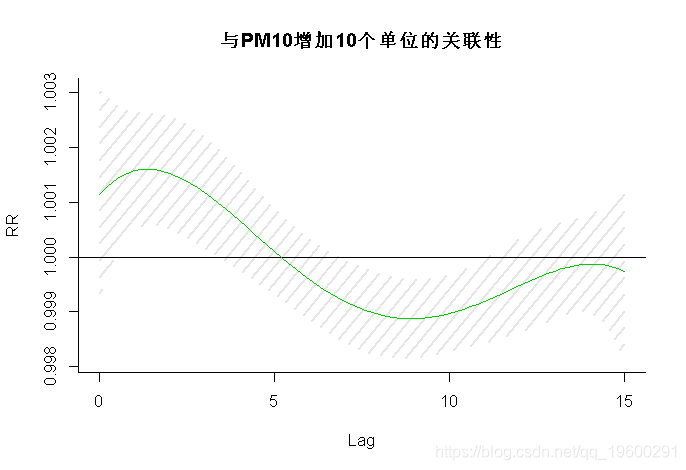
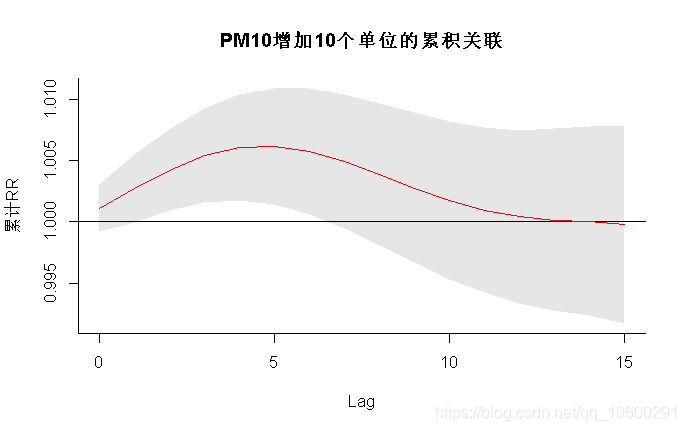
该函数包含带有存储结果的pred1.pm对象,参数“slices”定义了我们要绘制对应于相关维度中predictor和lag的特定值的关系图。var=10时,我显示PM10特定值的滞后响应关系,即10µgr/m3。该关联使用0µgr/m3的参考值来定义,从而为10个单位的增加提供预测特定关联。我还为第一个图选择了不同的颜色。PM10的特定值,即10 µgr / m3。使用0 µgr / m3的参考值定义此关联,从而为增加10个单位提供了特定于预测变量的关联。我还为第一个图选择了不同的颜色。参数cumul指示是否必须绘制以前保存在pred1.pm中的增量累积关联。结果如图1a-1b所示。置信区间被设置为参数ci的默认值“ area”。在左面板中,其他参数通过ci.arg传递给绘图函数polygon(),绘制阴影线作为置信区间。对这些曲线图的解释有两个方面:滞后曲线表示特定日期PM10增加10µgr/m3后未来每一天的风险增加(正向解释),或者过去每一天相同PM10对特定日期风险增加的贡献(反向解释)。图1a-1b中的曲线图表明,PM10风险的初始增加在较长的滞后时间被逆转。PM10在15天滞后时间内增加10个单位的总体累积效应(即将所有贡献相加至最大滞后时间)及其95%置信区间可通过pred1.pm中包含的对象allRRfit、allRRhigh和allRRlow提取,键入:
-
> pred1
-
10
-
0.9997563
-
> cbind(pred1.p
-
[1] 0.9916871 1.0078911
例2:季节分析
第二个例子的目的是说明数据仅限于特定季节的分析。这种分析的独特之处在于,假设数据是由不同年份的多个等距有序的多个季节序列组成,而不是一个单一的连续序列。在本例中,我使用第3节中已经看到的相同步骤,分别评估了臭氧浓度和温度对滞后5天和10天死亡率的影响。首先,我创建一个季节性时间序列数据集,只取夏季的区间,并将其保存在数据框ChicagonMaps中:
Sseas <- subset(NMMAPS, month %in% 6:9)
同样,我首先创建交叉基矩阵:
-
cb(o3, lag=5,
-
argvar=list(fun="thr",thr=40.3), arglag=list(fun="integer"),
-
group=year)
参数组指示定义多个序列的变量。每个序列必须是连续的、完整的和有序的。在这里,我假设O3的影响在达到40.3 µgr / m3之前为零,然后呈线性,并应用了高阈值参数化(fun =“ thr”)。对于温度,我使用一个双阈值,并假设在低于15°C且高于25°C时效果是线性的,并且在两者之间为零。阈值使用自变量thr.value(缩写为thr)进行选择,而未指定的自变量侧则将第一个交叉基准的默认值设置为“ h”,将第二个交叉基准的默认值设置为“ d”(给定)提供了两个阈值)。关于滞后维度,我为O3指定了一个不受约束的函数,为最多5天的每个滞后(fun =“ integer”)应用一个整数(默认情况下,最小滞后等于0)。对于温度,我定义了滞后0-1、2-5、6-10的3个区间。回归模型包括一年中某天和某天的自然样条,以便分别描述每年的季节性影响和长期趋势。特别是,与以前的分析相比,后者的自由度要小得多,因为它只需要捕获平稳的年度趋势即可。除此之外,以相同的方式进行估计和预测。代码为:
-
glm(death ~ cb2.o3 + cb2.temp + ns(doy, 4) + ns(time,3) + dow,
-
family=quasipoisson())
必须在其中指定要进行预测的值:在这里,我定义了0到65 µgr / m3(大约是臭氧分布范围)的整数,加上阈值和50.3µgr/m3的值,对应于阈值以上10个单位的增加。向量将自动排序。将自动选择由thr()建模的参考-反应曲线,并且可以不定义中心参数。我绘制了O3增加10个单位的预测因子特定滞后反应关系,但置信区间为80%,并且还绘制了总体累积暴露反应关系。
-
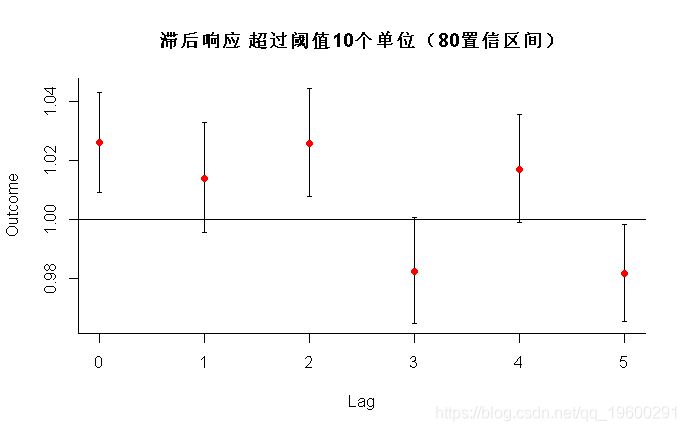
> plot(pred2.o3, "slices", main="滞后响应 超过阈值10个单位"(80置信区间))
-
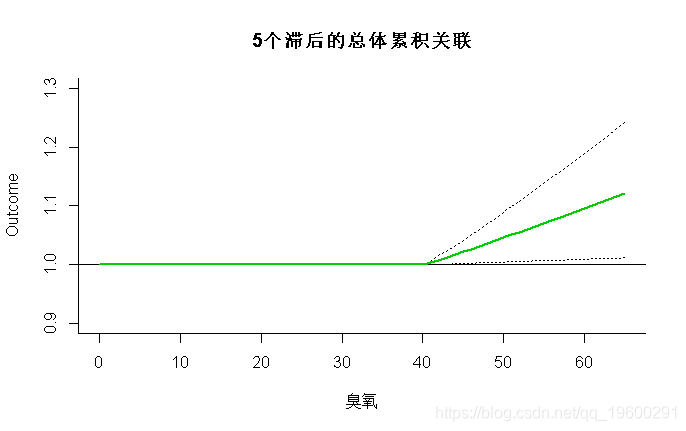
> plot(pred2.o3,"overall",xlab="臭氧", ci="l", main="5个滞后的总体累积关联")
在第一个语句中,参数ci =“ bars”指示与图1a-1b中的默认“区域”不同,置信区间用条形图表示。此外,参数ci.level = 0.80指出绘制80%的置信区间。最后,我根据参数类型和pch选择了带有特定符号的点。在第二个语句中,参数type =“ overall”表示必须绘制整体累积关联,置信区间为线,ylim定义y轴的范围,lwd表示直线的厚度。与前面的示例类似,通过ci.arg指定的参数列表来完善置信区间的显示,在这种情况下,将其传递给低级函数lines()。与上一个示例类似,我们可以从pred2.o3中提取臭氧浓度超过阈值(50.3−40.3µgr/m3)10个单位时的估计总体累积效应,以及95%置信区间:
-
> pred2.o3$allRRfit["50.3"]
-
50.3
-
1.047313
-
> cbind(allRRlow, allRRhigh)["50.3",]
-
[1] 1.004775 1.091652
可以将相同的图和计算应用于温度的冷热效应。例如,我们可以描述超过低阈值或高阈值1°C的风险增加。用户可以重复上述步骤执行此分析。
示例3:二维DLNM
在前面的例子中,空气污染(分别为PM10和O3)的影响被假定为完全线性或高于阈值的线性。这一假设有助于解释和表示这种关系:从不考虑预测因子的维度,并且很容易绘制出10个单位增加的特定或总体累积关联。相反,当考虑到温度的非线性相关性时,我们需要采用二维透视图来表示沿预测变量空间和滞后量非线性变化的关联。在此示例中,我指定了一个更复杂的DLNM,其中使用两个维度的平滑非线性函数来估计相关性。尽管关系的复杂性更高,但我们将看到指定和拟合模型以及预测结果所需的步骤与之前看到的简单模型完全相同,只需要选择不同的绘图即可。用户可以采用相同的步骤来研究先前示例中的温度影响,并扩展PM10和O3的图。在这种情况下,我运行DLNM来研究温度和PM10对死亡率的影响,分别达到滞后30和1。首先,我定义了交叉基矩阵。特别是,温度的交叉基是通过自然和非自然样条曲线指定的,使用来自软件包样条曲线的函数ns()和bs()。代码如下:
-
-
> varknots <- equalknots(temp,fun="bs",df=5,degree=2)
-
> lagknots <- logknots(30, 3)
-
-
预测空间的选择基函数是PM10效应的线性函数和温度5自由度的二次B样条(fun=“bs”),通过函数equalknots()选择,默认情况下,节点放置在预测器空间中的等间距值。关于滞后空间,我假设PM10的简单滞后0-1参数化(即直到滞后1的单个层,最小滞后默认等于0,保持默认值df=1),而我定义了另一个三次样条曲线,这一次温度滞后维度具有自然约束(fun=“ns”默认)。使用函数logknots(),将滞后样条曲线的节点放置在滞后对数比例中的等间距值处。温度和死亡率之间关系的估计、预测和绘图通过以下方式进行:
-
-
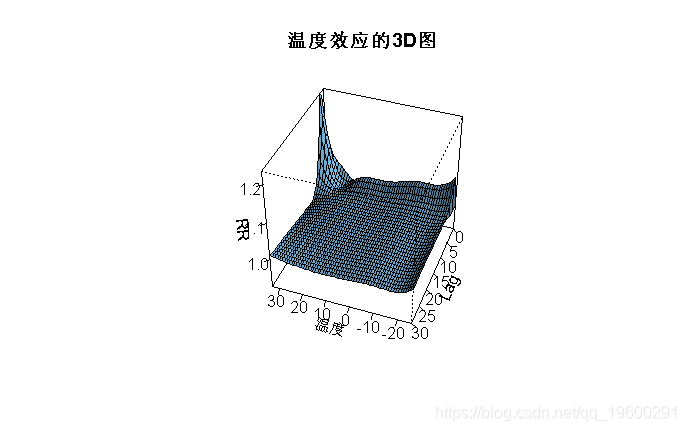
> plot(pred3.temp, xlab="温度" lphi=30,
-
main="温度效应的3D图")
-
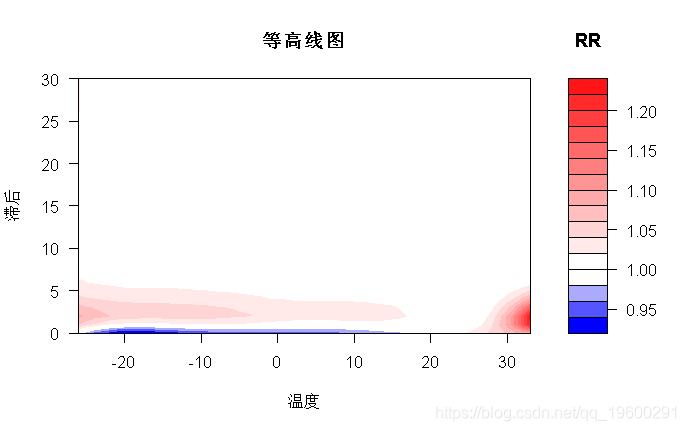
> plot(pred3.temp, "contour", xlab="温度",
-
plot.title=title("等高线图",xlab="温度",ylab="滞后"))
请注意,此处的预测值以21°C为中心,该点代表解释估计效应的参考。这里需要执行此步骤,因为该关系是使用没有明显参考值的非线性函数建模的。仅在crosspred()中使用参数by = 1来选择值,这些值定义了预测变量范围内的所有整数值。第一个绘图表达式生成一个3D绘图,如图3a所示,其中通过参数theta-phi-lphi获得了非默认的视角选项。第二个绘图表达式指定图3b中的轮廓图,其中标题和轴标签由参数plot.title和key.title选择。图3a-3b中的曲线图提供了二维暴露-滞后-反应关联的综合总结,但其在预测值或滞后的特定值下提供关联信息的能力有限。此外,由于三维图和等高线图中未报告估计关联的不确定性,因此它们也仅限于推理目的。通过绘制特定预测值和滞后值的效应面“切片”来提供更详细的分析。代码是:
-
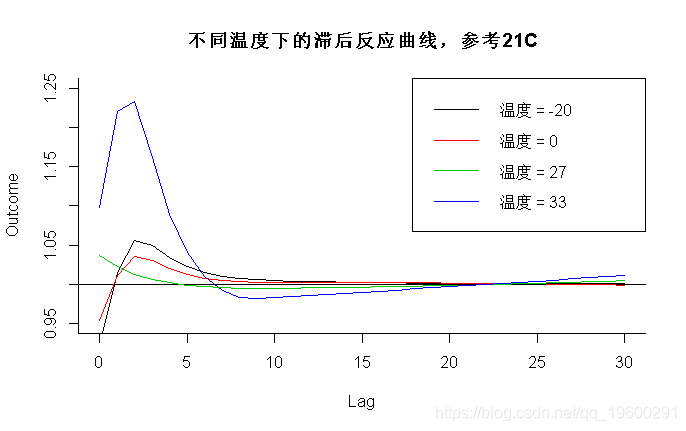
> plot(pred3.temp, "slices", var=-20,
-
main="不同温度下的滞后反应曲线,参考21C")
-
> for(i in 1:3) lines(pred3.temp, "slices", var=c(0,27,33)[i]
-
> legend("topright",paste("温度 ="
-
结果如图4a-4b所示。图4a说明了特定于-20℃、0℃、27℃和33℃的温和和极端冷热温度(参考21℃)的滞后反应曲线。图4b
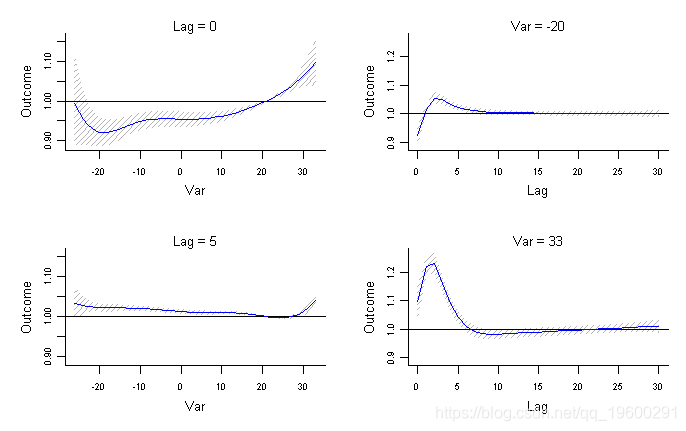
描述了滞后0和滞后5的暴露-反应关系(左列)以及温度-20℃和33℃下的滞后-反应关系(右列)。参数var和lag定义了要在图3a-3b中的效果表面上切割的“切片”的温度和滞后值。第一个表达式中的参数ci =“ n”表示不能绘制置信区间。在多面板图4b中,列表参数ci.arg用于绘制置信区间,将其作为阴影线增加灰色对比度,在此处更加明显。初步解释表明,低温比高温具有更长的死亡风险,但不是立即的,在滞后0时显示出“保护”效应。这种分析能力很难用更简单的模型实现,可能会丢失关联的重要细节。
示例4:降维DLNM
在最后一个例子中,我展示了如何使用函数crossreduce()将二维DLNM的拟合度降低到由一维基的参数表示的摘要。首先,我指定一个新的交叉基矩阵,运行模型并以通常的方式进行预测
指定的温度交叉基由双阈值函数和自然三次样条组成,分别以10°C和25°C的截止点作为预测器的维数,以对数标度中相等间距的节点值作为滞后量,如前一示例所示。可以对3个特定的摘要进行归约,即总的累积,滞后特定和预测变量特定的关联。前两个代表暴露-反应关系,而第三个代表滞后-反应关系。代码如下:
credu(cb4, model4)
在滞后5℃和33℃时,分别在两个空间中计算关联的减少。“crossreduce”类的3个对象包含相关空间中一维基的修改缩减参数,可与原始模型进行比较:
-
> length(coef(pred4))
-
[1] 10
-
> length(coef(redall)) ; length(coef(redlag))
-
[1] 2
-
[1] 2
-
> length(coef(redvar))
正如预期的那样,对于预测变量的空间,参数数量已减少到2(与双阈值参数化一致),对于滞后空间,参数数量已减少到5(与自然三次样条曲线基的维度一致)。但是,原始拟合和简化拟合的预测是相同的,如图5a所示:
-
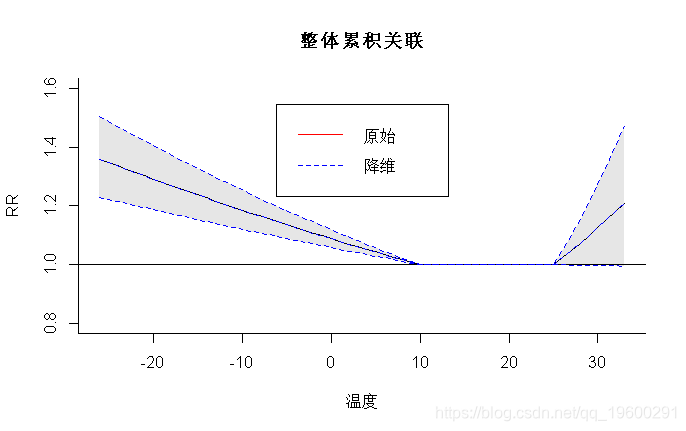
> plot(pred4, "overall", xlab="温度", ylab="RR",
-
ylim=c(0.8,1.6), main="整体累积关联")
-
> lines(redall, ci="lines",col=4,lty=2)
-
> legend("top",c("原始","降维"),col=c(2,4),lty=1:2,ins=0.1)
这个过程也可以通过重新构造原始的一维基和预测给定修正参数的关联来阐明。作为一个例子,我使用onebasis()为滞后空间再现了自然三次样条曲线,并预测结果:
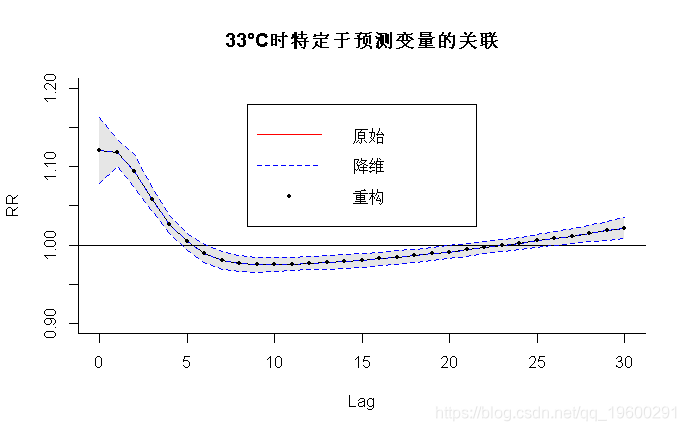
样条基是基于对应于滞后0:30的整数值计算的,节点与原始交叉基的值相同,并且不居中,以截距作为滞后基的默认值。使用修正后的参数对33℃的预测值进行计算。原始、简化和重建预测值的相同拟合如图5b所示,由以下公式得出:
-
> plot(pred4, "slices", var=33,
-
main="33°C时特定于预测变量的关联")
-
-
> legend("top",c("原始","降维","重构"),

最受欢迎的见解
1.在python中使用lstm和pytorch进行时间序列预测
2.python中利用长短期记忆模型lstm进行时间序列预测分析