原文链接:http://tecdat.cn/?p=21825
原文出处:拓端数据部落公众号
假设检验的基本原理是小概率原理,即我们认为小概率事件在一次试验中实际上不可能发生。
多重比较的问题
当同一研究问题下进行多次假设检验时,不再符合小概率原理所说的“一次试验”。如果在该研究问题下只要有检验是阳性的,就对该问题下阳性结论的话,对该问题的检验的犯一类错误的概率就会增大。如果同一问题下进行n次检验,每次的检验水准为α(每次假阳性概率为α),则n次检验至少出现一次假阳性的概率会比α大。假设每次检验独立的条件下该概率可增加至
![]()
常见的多重比较情景包括:
- 多组间比较
- 多个主要指标
- 临床试验中期中分析
- 亚组分析
控制多重比较谬误(Familywise error rate):Bonferroni矫正
Bonferroni法得到的矫正P值=P×n
Bonferroni法非常简单,它的缺点在于非常保守(大概是各种方法中最保守的了),尤其当n很大时,经过Bonferroni法矫正后总的一类错误可能会远远小于既定α。
控制错误发现率:Benjamini & Hochberg法
简称BH法。首先将各P值从小到大排序,生成顺序数
排第k的矫正P值=P×n/k
另外要保证矫正后的各检验的P值大小顺序不发生变化。
怎么做检验
R内置了一些方法来调整一系列p值,以控制多重比较谬误(Familywise error rate)或控制错误发现率。
Holm、Hochberg、Hommel和Bonferroni方法控制了多重比较谬误(Familywise error rate)。这些方法试图限制错误发现的概率(I型错误,在没有实际效果时错误地拒绝无效假设),因此都是相对较保守的。
方法BH(Benjamini-Hochberg,与R中的FDR相同)和BY(Benjamini & Yekutieli)控制错误发现率,这些方法试图控制错误发现的期望比例。
请注意,这些方法只需要调整p值和要比较的p值的数量。这与Tukey或Dunnett等方法不同,Tukey和Dunnett也需要基础数据的变异性。Tukey和Dunnett被认为是多重比较谬误(Familywise error rate)方法。
要了解这些不同调整的保守程度,请参阅本文下面的两个图。
关于使用哪种p值调整度量没有明确的建议。一般来说,你应该选择一种你的研究领域熟悉的方法。此外,可能有一些逻辑允许你选择如何平衡犯I型错误和犯II型错误的概率。例如,在一项初步研究中,你可能希望保留尽可能多的显著值,来避免在未来的研究中排除潜在的显著因素。另一方面,在危及生命并且治疗费用昂贵的医学研究中,得出一种治疗方法优于另一种治疗方法的结论之前,你应该有很高的把握。
具有25个p值的多重比较示例
-
### --------------------------------------------------------------
-
### 多重比较示例
-
### --------------------------------------------------------------
-
-
Data = read.table(Input,header=TRUE)
按p值排序数据
Data = Data[order(Data$Raw.p),]
检查数据是否按预期的方式排序

执行p值调整并添加到数据框
-
Data$Bonferroni =
-
p.adjust(Data$Raw.p,
-
method = "bonferroni")
-
-
Data$BH =
-
p.adjust(Data$Raw.p,
-
method = "BH")
-
-
Data$Holm =
-
p.adjust(Data$ Raw.p,
-
method = "holm")
-
-
Data$Hochberg =
-
p.adjust(Data$ Raw.p,
-
method = "hochberg")
-
-
Data$Hommel =
-
p.adjust(Data$ Raw.p,
-
method = "hommel")
-
-
Data$BY =
-
p.adjust(Data$ Raw.p,
-
method = "BY")
-
-
Data
-
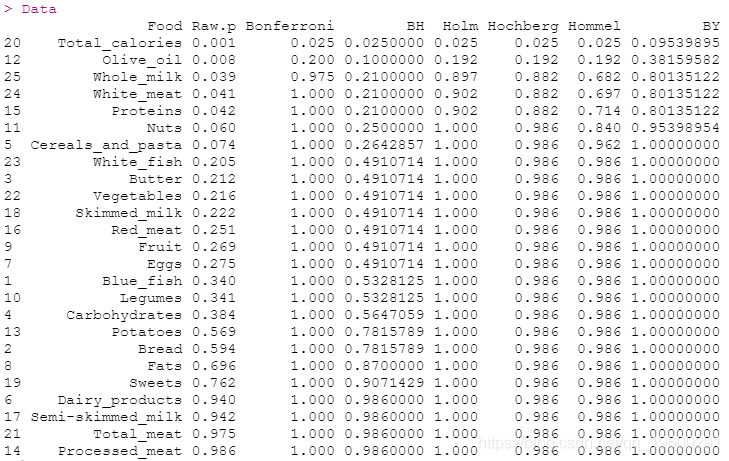
绘制图表
-
plot(X, Y,
-
xlab="原始的p值",
-
ylab="矫正后的P值"
-
lty=1,
-
lwd=2
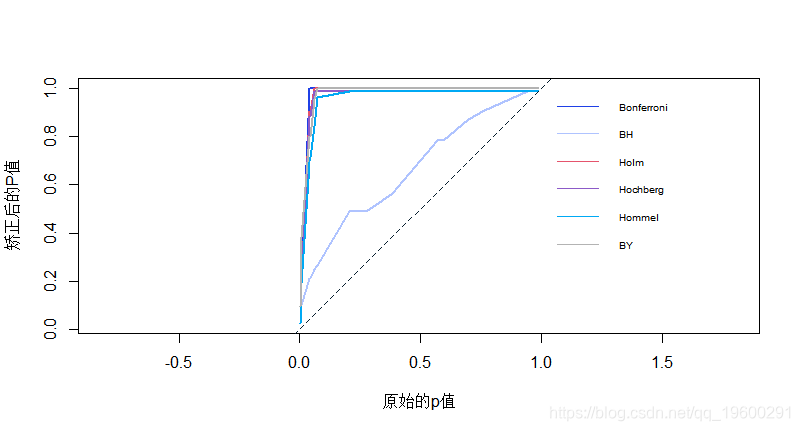
调整后的p值与原始的p值的图为一系列的25个p值。虚线表示一对一的线。
5个p值的多重比较示例
-
### --------------------------------------------------------------
-
### 多重比较示例,假设示例
-
### --------------------------------------------------------------
-
Data = read.table(Input,header=TRUE)
执行p值调整并添加到数据帧
-
Data$Bonferroni =
-
p.adjust(Data$Raw.p,
-
method = "bonferroni")
-
-
Data$BH =
-
signif(p.adjust(Data$Raw.p,
-
method = "BH"),
-
4)
-
-
Data$Holm =
-
p.adjust(Data$ Raw.p,
-
method = "holm")
-
-
Data$Hochberg =
-
p.adjust(Data$ Raw.p,
-
method = "hochberg")
-
-
Data$Hommel =
-
p.adjust(Data$ Raw.p,
-
method = "hommel")
-
-
Data$BY =
-
signif(p.adjust(Data$ Raw.p,
-
method = "BY"),
-
4)
-
-
Data
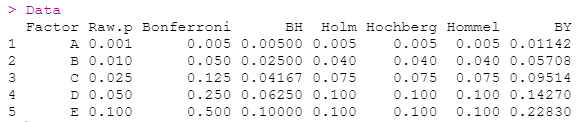
绘制(图表)
-
-
-
plot(X, Y,
-
type="l",
-
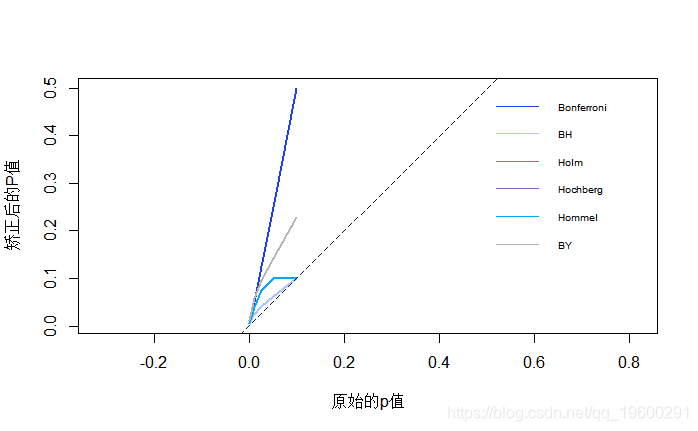
调整后的p值与原始p值在0到0.1之间的一系列5个p值的绘图。请注意,Holm和Hochberg的值与Hommel相同,因此被Hommel隐藏。虚线表示一对一的线。

最受欢迎的见解
1.Matlab马尔可夫链蒙特卡罗法(MCMC)估计随机波动率(SV,Stochastic Volatility) 模型
3.WinBUGS对多元随机波动率模型:贝叶斯估计与模型比较
4.R语言回归中的hosmer-lemeshow拟合优度检验