拓端tecdat：R语言BUGS序列蒙特卡罗SMC、马尔可夫转换随机波动率SV模型、粒子滤波、METROPOLIS HASTINGS采样时间序列分析

原文链接：http://tecdat.cn/?p=24162

原文出处：拓端数据部落公众号

在这个例子中，我们考虑马尔可夫转换随机波动率模型。

统计模型

设 yt为因变量，xt 为 yt 未观察到的对数波动率。对于 t≤tmax，随机波动率模型定义如下

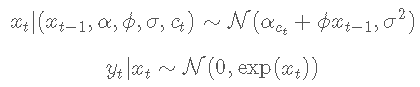
状态变量 ct 遵循具有转移概率的二状态马尔可夫过程

N(m,σ2)表示均值 m 和方差 σ2的正态分布。

BUGS语言统计模型

文件内容 'vol.bug'：

dlfie = 'vol.bug' #BUGS模型文件名

设置

设置随机数生成器种子以实现可重复性

set.seed(0)

加载模型和数据

模型参数

1.  
    
2.  
   dt = lst(t_mx=t_mx, sa=sima,
3.  
   alha=alpa, phi=pi, pi=pi, c0=c0, x0=x0)

解析编译BUGS模型，以及样本数据

modl(mol_le, ata,sl_da=T)

绘制数据

plot(1:tmx, y, tpe='l',xx = 'n')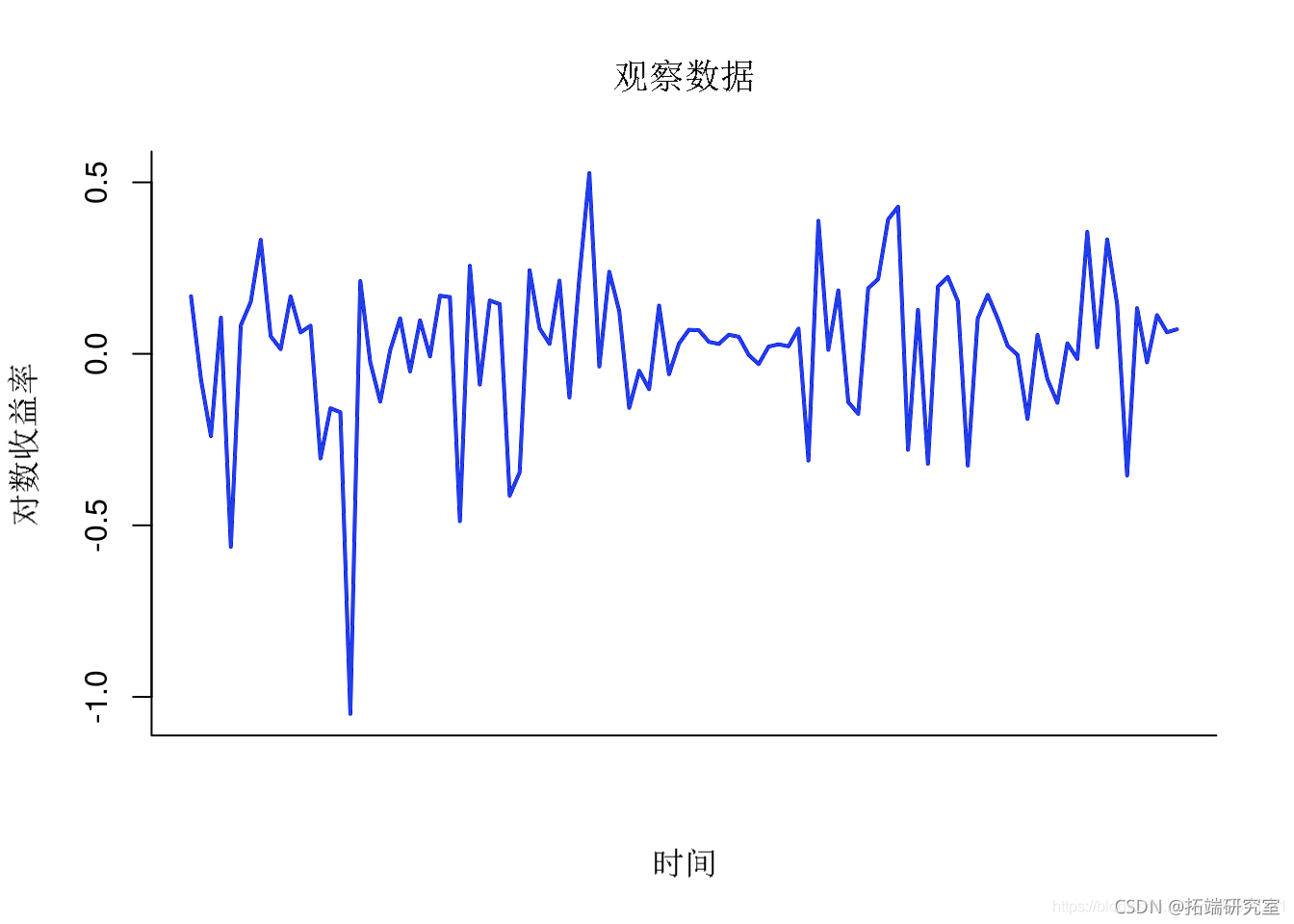

对数收益率

序列蒙特卡罗Sequential Monte Carlo

运行

1.  
   n= 5000 # 粒子的数量
2.  
   var= c('x') # 要监测的变量
3.  
   out = smc(moe, vra, n)

模型诊断

diagnosis(out)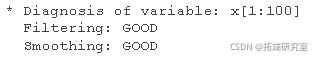

绘图平滑 ESS

1.  
   plt(ess, tpe='l')
2.  
   lins(1:ta, ep(0,tmx))

SMC：SESS

绘制加权粒子

1.  
   plt(1:tax, out,)
2.  
   for (t in 1:_ax) {
3.  
   vl = uiq(valest,])
4.  
   wit = sply(vl, UN=(x) {
5.  
   id = utm$$sles[t,] == x
6.  
   rtrn(sm(wiht[t,ind]))
7.  
   })
8.  
   pints(va)
9.  
   }
10.  
    lies(1t_x, at$xue)
11.  
     

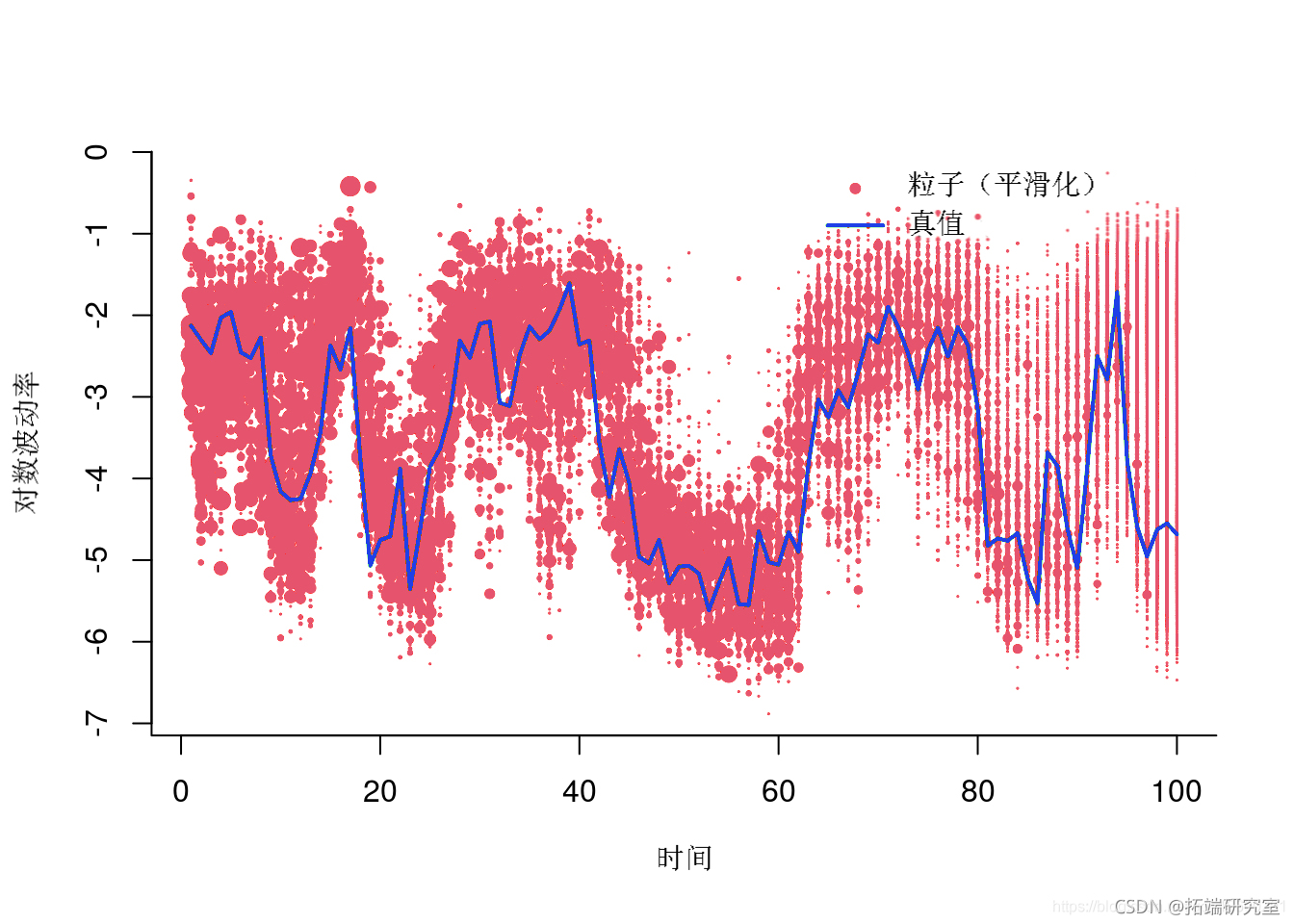
粒子（平滑）

汇总统计

summary(out)

绘图滤波估计

1.  
   men = mean
2.  
   qan = quant
3.  
    
4.  
   x = c(1:tmx, _a:1)
5.  
   y = c(fnt, ev(x__qat))
6.  
   plot(x, y)
7.  
   pln(x, y, col)
8.  
   lines(1:tma,x_ean)
9.  
    

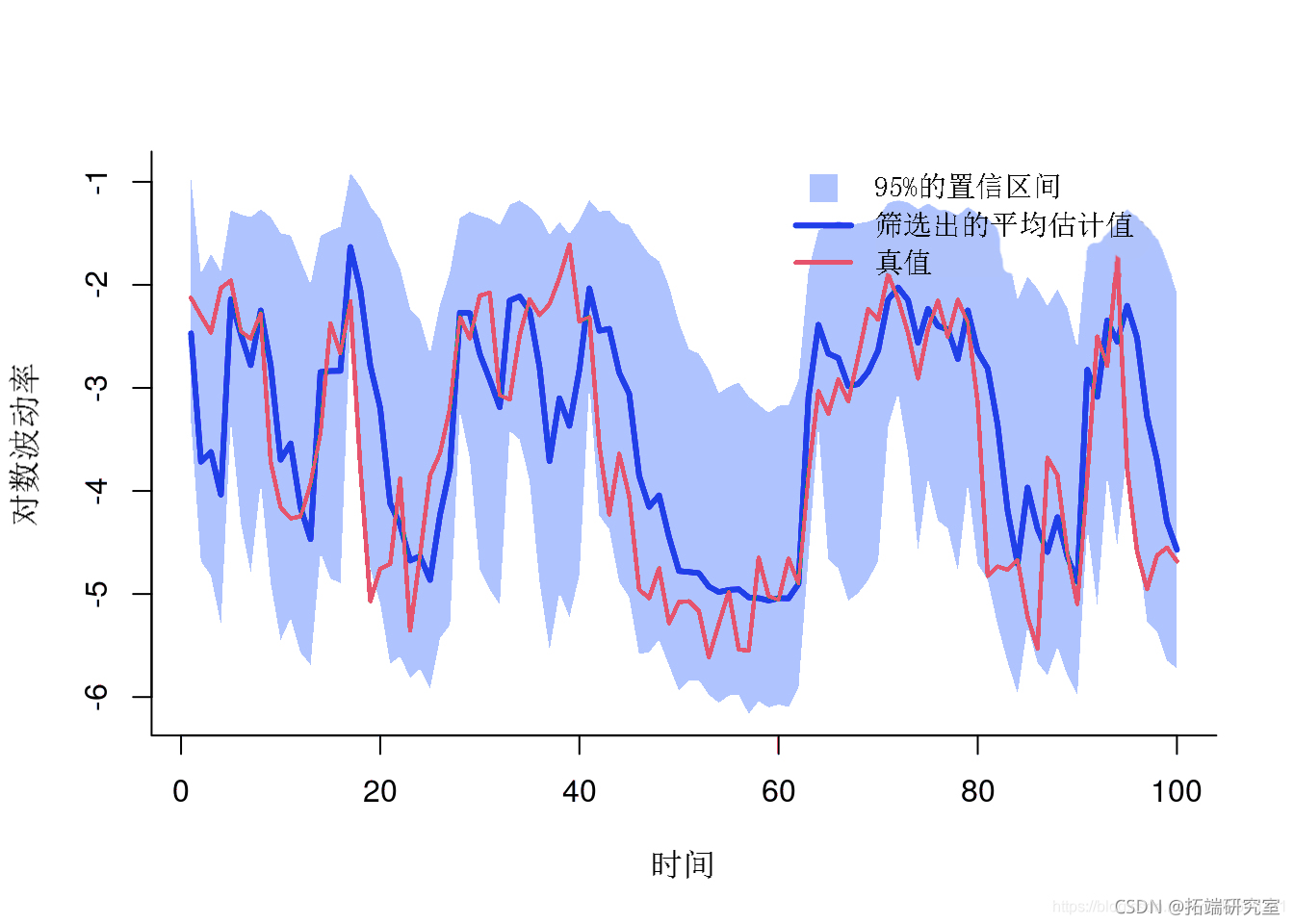
滤波估计

绘图平滑估计

1.  
    
2.  
   plt(x,y, type='')
3.  
    
4.  
   polgon(x, y)
5.  
   lins(1:tmx, mean)
6.  
    

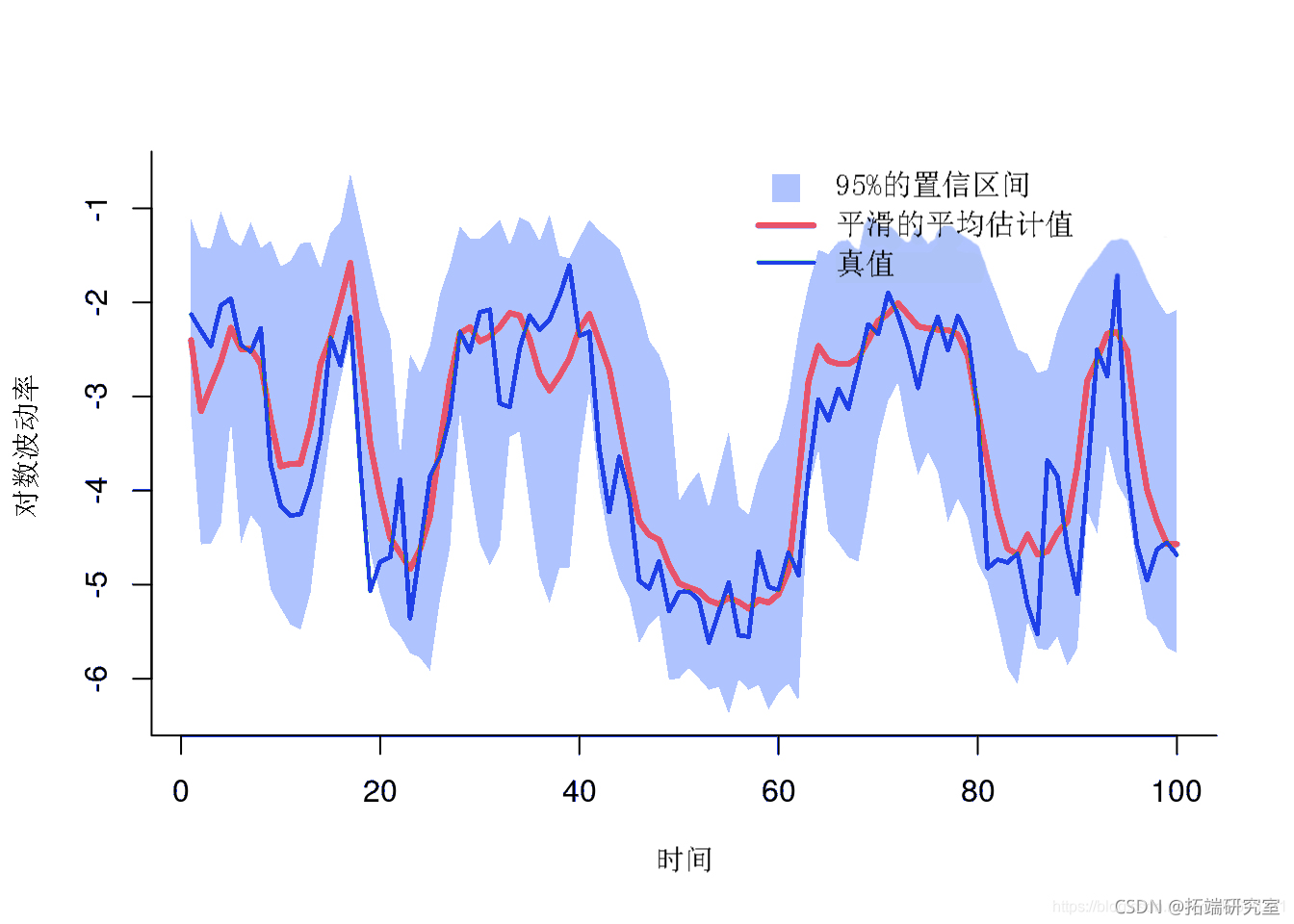
平滑估计

边缘滤波和平滑密度

1.  
   denty(out)
2.  
   indx = c(5, 10, 15)
3.  
    
4.  
   for (k in 1:legh) {
5.  
   inex
6.  
   plt(x)
7.  
   pints(xtrue[k])
8.  
   }
9.  
    

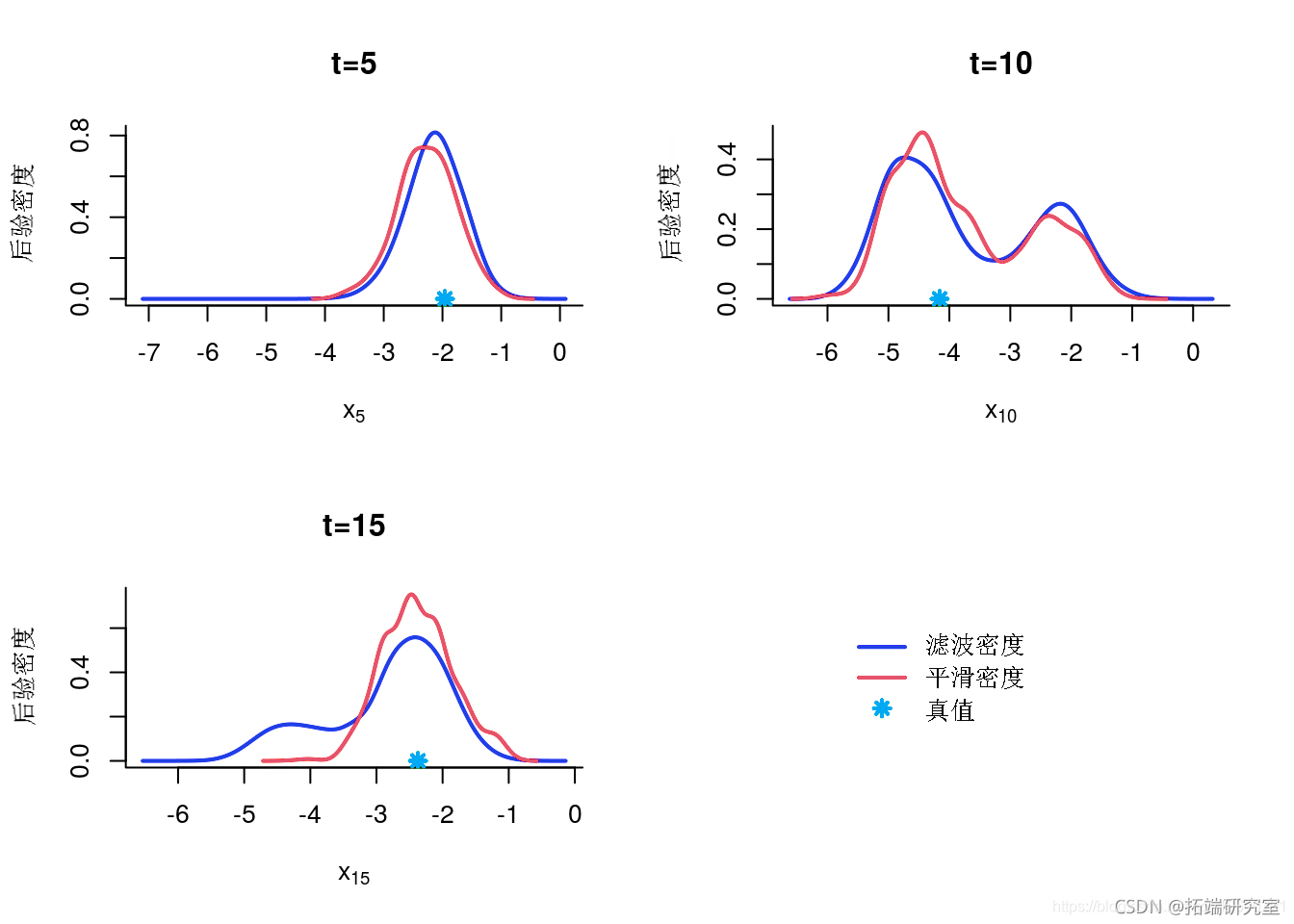
边缘后验

粒子独立 Metropolis-Hastings

运行

mh = mit(mol, vre)

mh(bm, brn, prt) # 预烧迭代

mh(bh, ni, n_at, hn=tn) # 返回样本

一些汇总统计

smay(otmh, pro=c(.025, .975))

后验均值和分位数

1.  
   mean
2.  
   quant
3.  
   plot(x, y)
4.  
    
5.  
   polo(x, y, border=NA)
6.  
   lis(1:tax, mean)
7.  
    

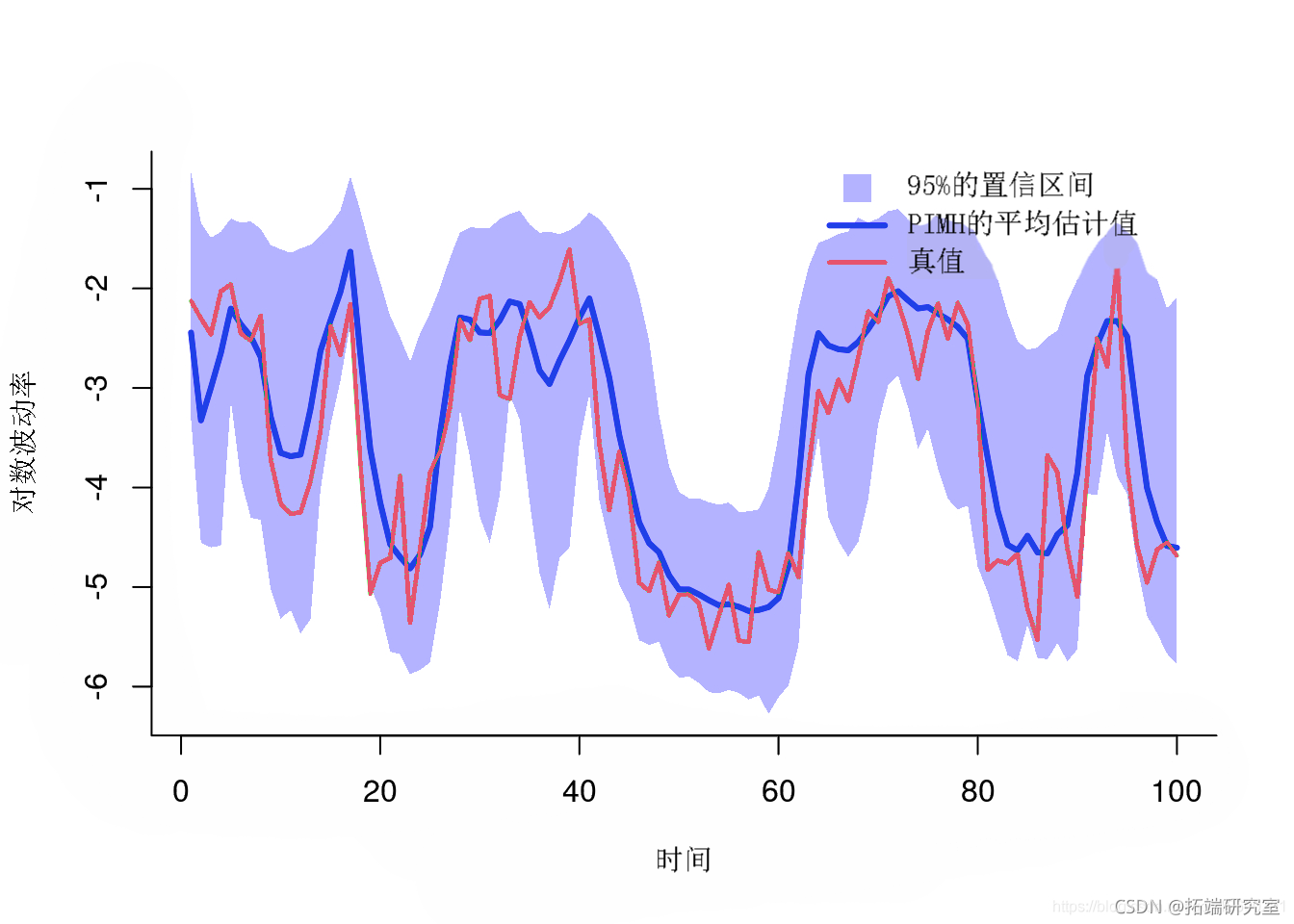
后验均值和分位数

MCMC 样本的踪迹图

1.  
    
2.  
   for (k in 1:length {
3.  
   tk = idx[k]
4.  
   plot(out[tk,]
5.  
   )
6.  
   points(0, xtetk)
7.  
   }

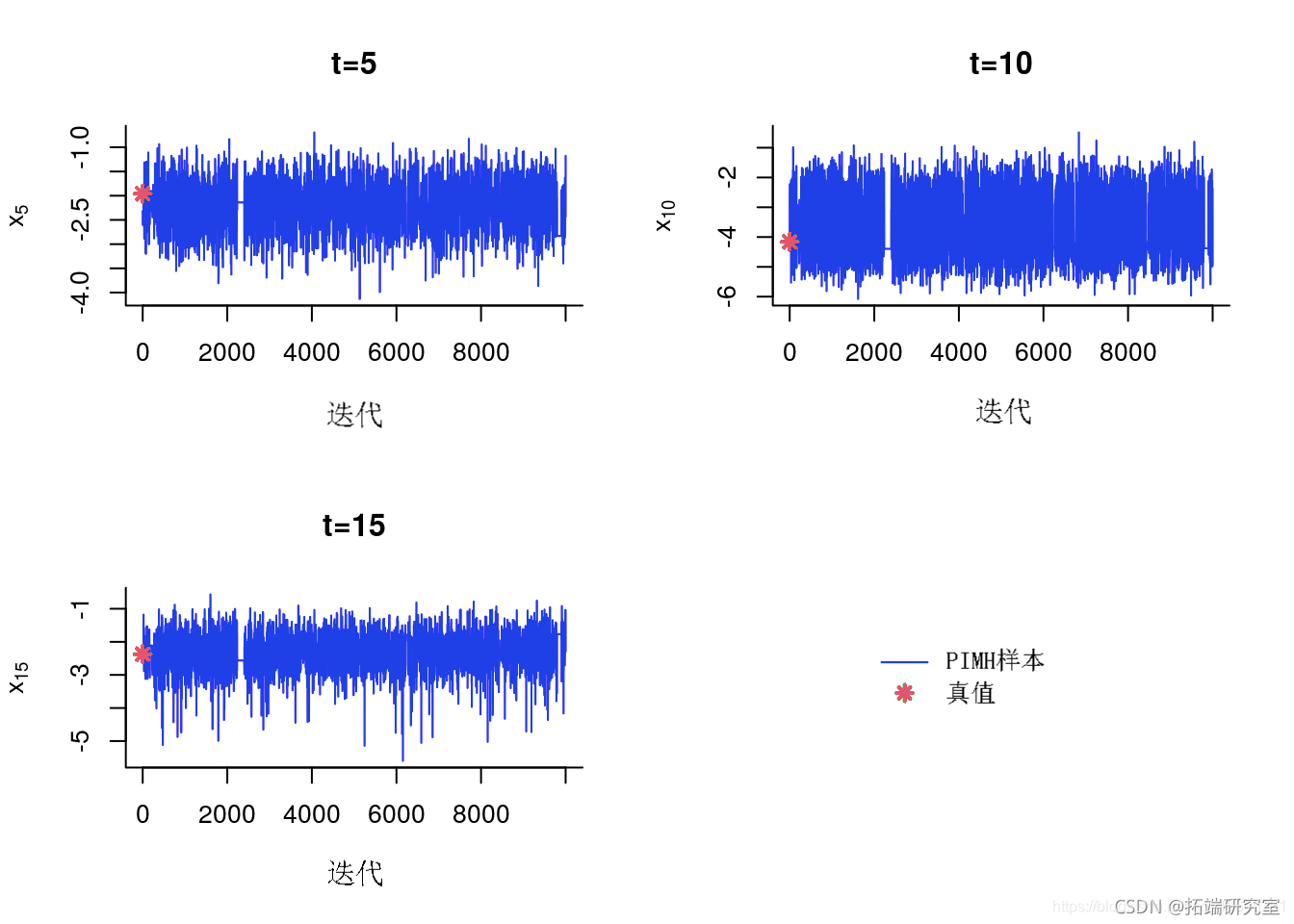
跟踪样本

后验直方图

1.  
    
2.  
   for (k in 1:lngh) {
3.  
   k = inex[k]
4.  
   hit(mh$x[t,])
5.  
   poits(true[t])
6.  
   }

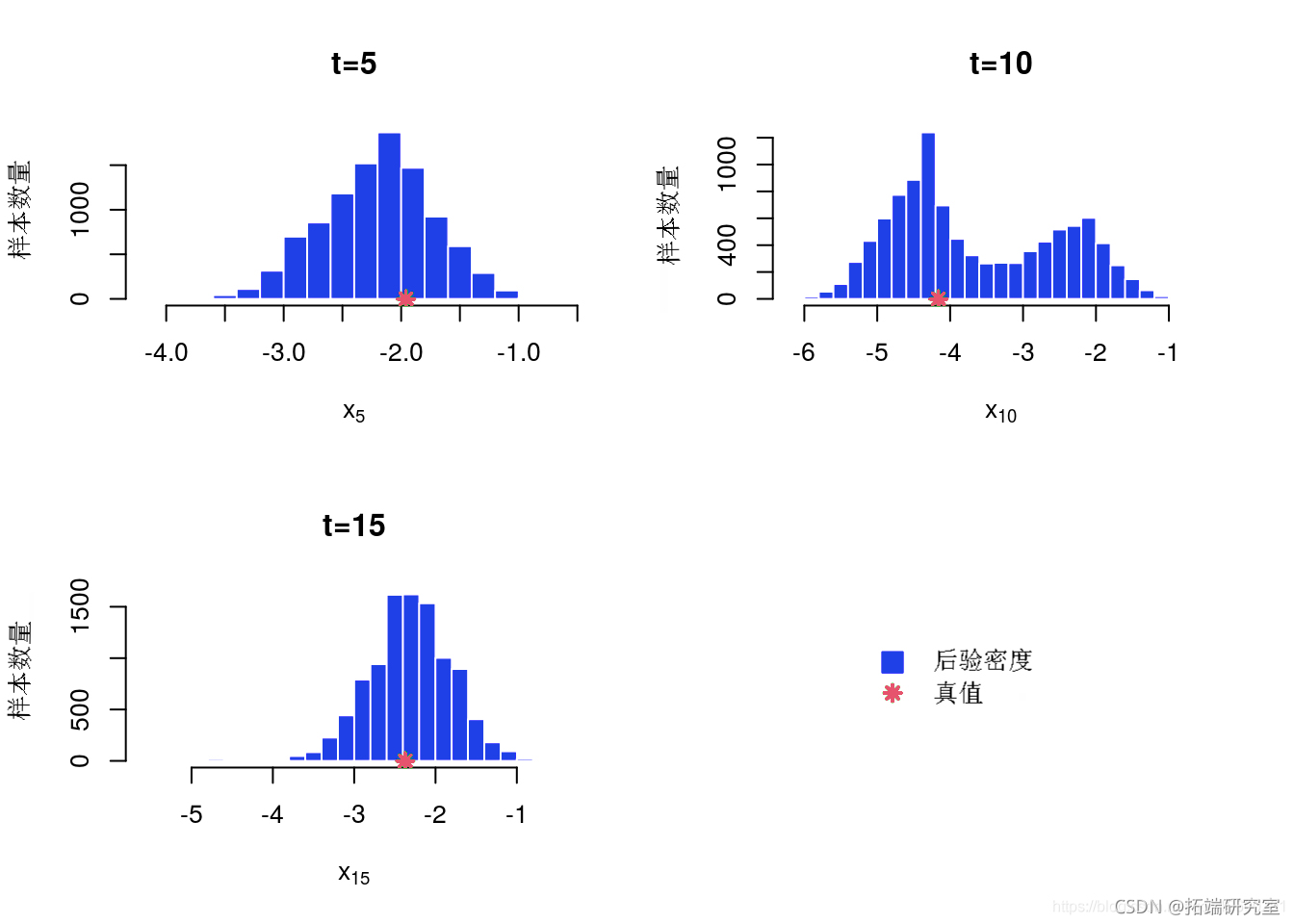
后边缘直方图

后验的核密度估计

1.  
   for (k in 1:lnth(ie)) {
2.  
   idx[k]
3.  
   desty(out[t,])
4.  
   plt(eim)
5.  
   poit(xtu[t])
6.  
   }

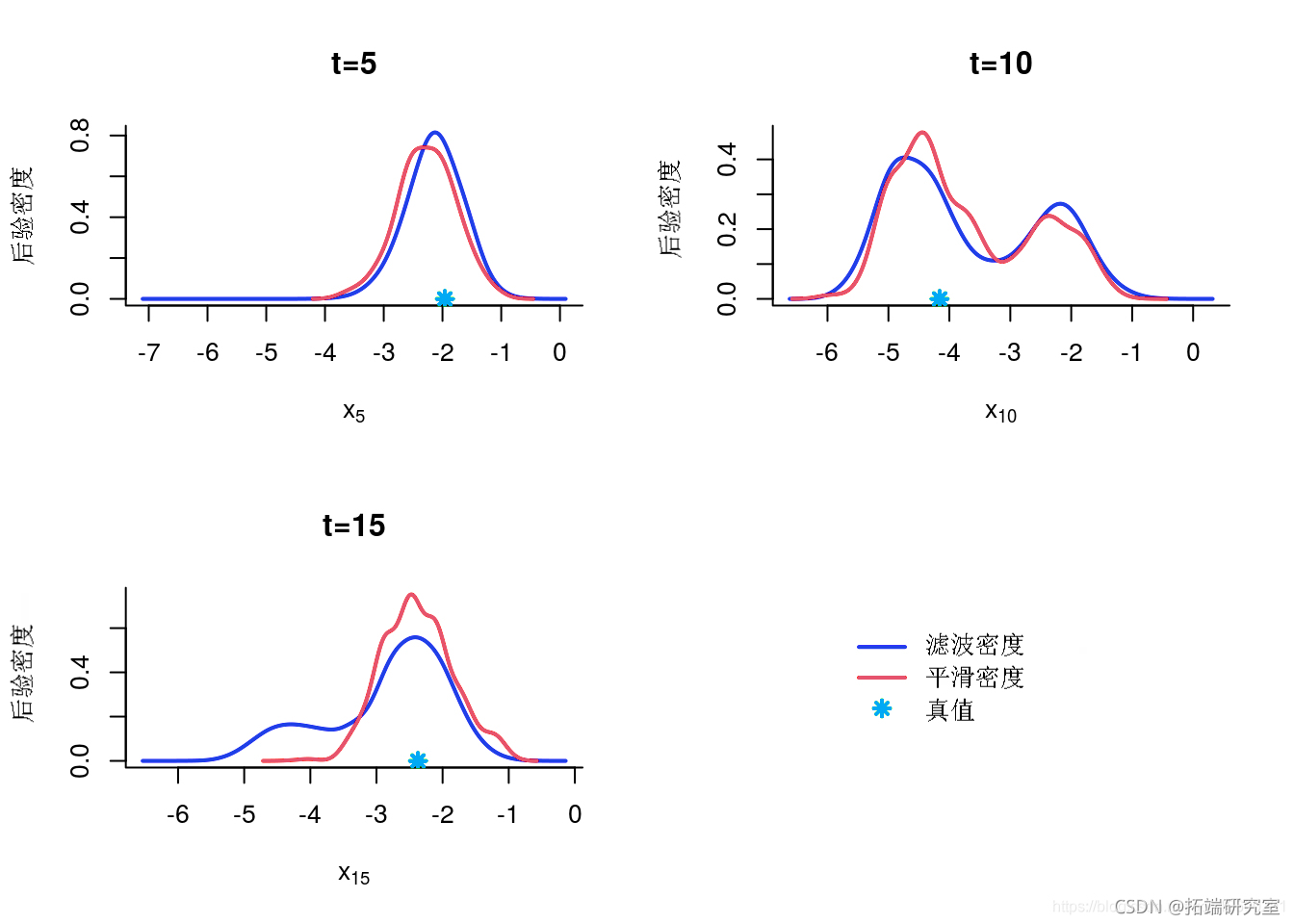
KDE 后验边缘估计

敏感性分析

我们想研究对参数 α 值的敏感性

算法参数

1.  
   nr = 50 # 粒子的数量
2.  
   gd <- seq(-5,2,.2) # 一个成分的数值网格
3.  
   A = rep(grd, tes=leg) # 第一个成分的值
4.  
   B = rep(grd, eah=lnh) # 第二个成分的值
5.  
   vaue = ist('lph' = rid(A, B))

运行灵敏度分析

sny(oel,aaval, ar)

绘制对数边缘似然和惩罚对数边缘似然

1.  
    
2.  
   # 通过阈值处理避免标准化问题
3.  
   thr = -40
4.  
   z = atx(mx(thr, utike), row=enth(rd))
5.  
    

1.  
   plot(z, row=grd, col=grd,
2.  
   at=sq(thr))

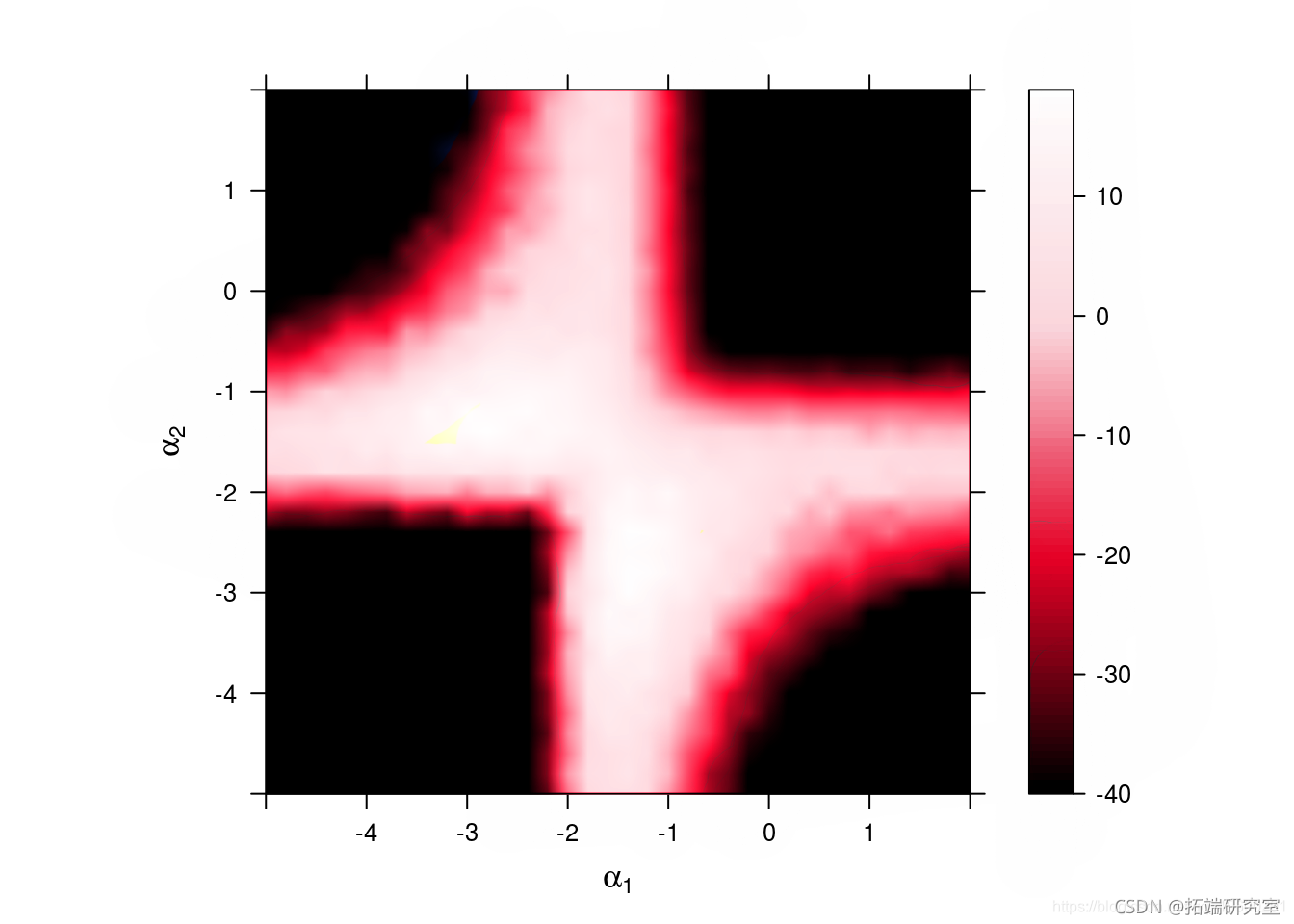
敏感性：对数似然

---

最受欢迎的见解

1.HAR-RV-J与递归神经网络（RNN）混合模型预测和交易大型股票指数的高频波动率

2.WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

3.波动率的实现：ARCH模型与HAR-RV模型

4.R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测

5.使用R语言随机波动模型SV处理时间序列中的随机波动率

6.R语言多元COPULA GARCH 模型时间序列预测

7.R语言基于ARMA-GARCH过程的VAR拟合和预测

8.R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型

9.R语言对S＆P500股票指数进行ARIMA + GARCH交易策略