色差应该控制在多少范围之类呢

CMF设计军团 · 中国设计界最为专注的CMF原创型研究平台
endlessring CMF设计军团
CMF | 如果要两个物体没有色差,它们的色坐标之差应该控制在多少范围内?麦克亚当圈就专门讨论这个问题~
我们在上三期介绍了CIE 1931色度图(文末有链接),一个新的问题就来了:如果要两个物体没有色差,它们的色坐标之差应该控制在多少范围内?
麦克亚当圈就专门讨论这个问题。
这个东西其实背景略复杂。。。
简单点说,就是,以麦克亚当为代表的科学家,他们针对颜色宽容度做了一系列实验。其结论就是,以圈圈里面的这个点为中心(目标色),一旦待对比的样品色品坐标超出了这个圈圈的范围,99%以上都会认为有色差。
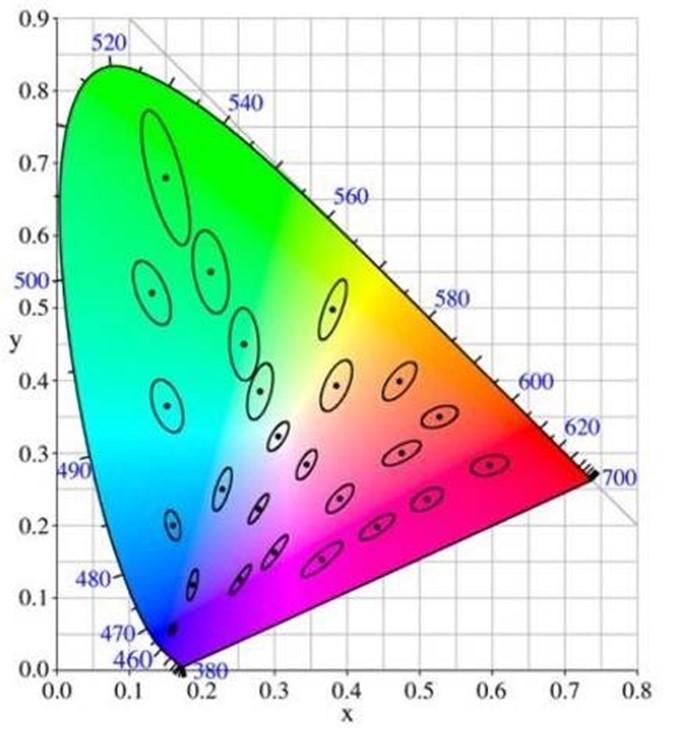
图里的这些圈圈就是所谓的"麦克亚当圈",因为是椭圆形的,所以也叫麦克亚当椭圆,MacAdam ellipse)
这个图告诉我们两件事:
1. CIE 1931色空间是一个不均匀的色空间;
2. 人对颜色宽容度的判断,跟我们一般的直觉不同,它并不是一个确定事件,而是一个服从概率分布的随机事件(不能稳定的复现实验结果,而是有波动)。
❶ 首先说说第一点:色空间不均匀。
麦克亚当圈在色度图不同的位置大小会不同,这就意味着在不同颜色区域颜色宽容度*不一样。比如,绿色部分的圈比较大,而蓝色部分很小。这意味着,在绿色区域,即使Δx和Δy很大,也可能看起来是差不多的绿。而在蓝色区域,即便Δx和Δy只有一丢丢,也是不同的蓝色。因此CIE 1931是个不均匀的色空间。
颜色宽容度* ,color tolerance
色度图上,人眼感觉不到颜色差异的变化范围,被称为颜色宽容度。
当我们要复现某一个颜色的时候,要完全准确的复现色度图上的某一个点其实是非常困难的,但在一定的误差(tolerance)范围内的复现则是可行的。
对颜色宽容度的研究,是颜色复现工作的重要理论基础。
❷ 这些圈圈并不是圆,而是椭圆。也就是说,x和y方向上的颜色宽容度也不一样。
并且,有的地方是x方向的宽容度高,有的地方是y方向的宽容度高。因为这些椭圆的方向角也是随位置不同而不同的。
▌ 这会带来什么问题呢?
现在假设我们有一个颜色A和颜色B。它们的色品坐标都已经测出来了,那么Δx和Δy都知道了。
如果CIE 1931是个均匀的色空间,那么麦克亚当圈就应该是一个正圆形。假如Δx和Δy在某个阈值范围之内,就可以知道它们看起来应该是一个颜色。反之,两个颜色就是有色差的。
可是,事实上CIE 1931却是不均匀的。。。所以即便是我们已经知道颜色A和B的色坐标,它们看起来有没有差别也还是没法确定。。。
▌ 那么我们费这么大劲,把测量颜色的量化工作做到如此地步*,又意义何在呢?!
*精确测量色坐标,需要用带标准光源的分光式光谱仪,设备又贵又笨重,还需要经常校准(校准也是一大笔钱哇!),测起来速度也慢,测试数据还要精确到小数点后四位。。。
即便是专门为某些特定应用场合设计的、轻便型、分色式色度计,也不便宜。。。玩过校色仪的同志都懂 。。。( ̄▽ ̄)"
所以,CIE一系列的后续发展,基本都是为了要解决这个问题。
一切的一切,就是要让麦克亚当圈从椭圆变成正圆!
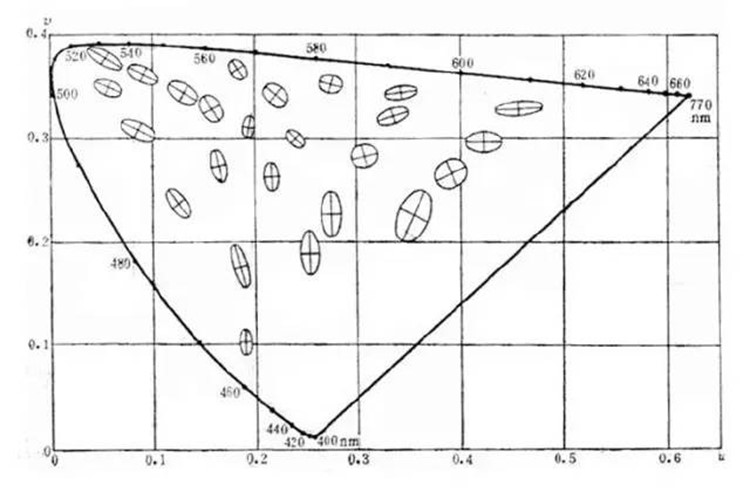
CIE 1960 UCS图上的麦克亚当椭圆
圆了不少,但也还是不完美。
因为真正(理论上)理想的均匀色品图是一个曲面,而不是一个平面。所以在平面上只能找到一个近似均匀的色品图(有点类似要在地图上画地球仪的感觉)。
唉,将就一下咯。。。
由此,在均匀的色空间里,更容易得到有效的色差公式。
以更均匀的L*a*b*色空间为例,颜色(L*1a*1b*1)和颜色(L*2a*2b*2)之间的色差ΔE*ab(CIE LAB色差)就是简单的算一下两点之间的距离就可以了:
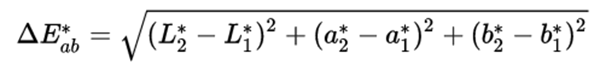
ΔE,读作Delta E。
Δ是希腊字母,念作delta,经常用来表示"差值"的意思。
而这个E,则来自于德语的Empfindung,意思是"感知"。
用ΔE来标注色差的传统,源自色度学的两位先驱,亥姆霍兹(Hermann von Helmholtz)和赫林(Ewald Hering),他们都是德国人。。。
当然,色度学作为一门发展中的学科,对色差的计算也还在升级打怪中(怎么可能这么简单就结束了,呵呵。。。)
考虑到麦克亚当圈在Lab空间里其实也是椭圆,所以即便是ΔE的值都是1(单位NBS),人感受到的色差大小也会略有差异。因此ΔE*ab引入了代表椭圆的大小和偏心率的权重函数,升级为ΔE*cmc(CMC(l:c)色差)。
进一步,由于观察条件的不同,色差的主观感受也不同。因此又引入了代表观察条件的参数因子,色差公式升级为ΔE*94(CIE 94色差,1995年公布)。
现在的终极版本则是考虑得更细致、参数更多的ΔE*00(CIE 2000色差,2000年公布)。这里就不放公式长什么样了,反正就是很长很长很长的一串。。。有机会再详细介绍(啊,也许吧。。。
▌ 啰嗦了这么长一段,我想表达的重点就是:
大家以后看到ΔE这个色差参数的时候,还需要留意一下具体用的是哪一个算法。
如果没有特别说明,就应该是目前应用最广泛的ΔE*ab,它的色差单位是NBS(美国国家标准局的英文缩写,National Bureau of Standards)。然而并不是所有的色差值单位都是NBS,不同的公式,单位就不一样,不同体系下的色差值也没法简单地换算。。。
而在CIE LAB色差ΔE*ab的值都一样的情况下,人对色差的感受也不一定一样。它是一个相对准确、而非绝对准确的值,一个年轻的、还在发展完善中的色度学参数。。。
至于第二点,人对色差感受的随机性,则更难理解了。。。
首先,麦克亚当圈是分阶数的,我们在上图看到的麦克亚当圈示意图其实是个五阶的图,是一阶麦克亚当圈的十倍大!
可是这个"阶"是什么意思呢?
所谓的一阶,就是统计学上说的标准差。
那这个标准差又是什么意思呢?
简单说就是,色坐标一旦超过这个一阶的圈,会有大概七成(68.3%)的概率被判定为有色差。
▌ 简单回顾一下相关统计学背景知识
正态分布(Normal distribution),也称"常态分布",又名高斯分布(Gaussian distribution)。它是应用最广泛的一种连续型分布,大部分的自然现象及人为程序是呈现正态分布的,或是经由转换后可以用正态分布的形式来表现。
若随机变量X服从一个位置参数为μ、尺度参数为σ 的概率分布,且其概率密度函数为
则这个随机变量X就称为正态随机变量,称为X服从正态分布。
它的分布曲线呈钟形,因此又被称为"钟形曲线"。
长这样:

在曲线下的区段面积可用来估计一特定事件发生之累计概率。
当样本值和样本平均值的误差在一个标准差σ以内时,发生的概率为68.3%;而在一个标准差σ以外的发生概率则为1-68.3%=31.7%.
依此类推,误差超出的标准差个数越多,概率迅速减少。
当样本值和均值的误差在6个σ以上时,发生概率只有百万分之三左右。这就是六西格玛管理的理论基础。
一阶麦克亚当圈的"一阶",就是指+/-1 s.d.(正负两个方向的标准差σ,standard deviations)。
每一个字都能看懂,可是这到底是什么意思。。。
我们先来看一下麦克亚当的实验是怎么做的。
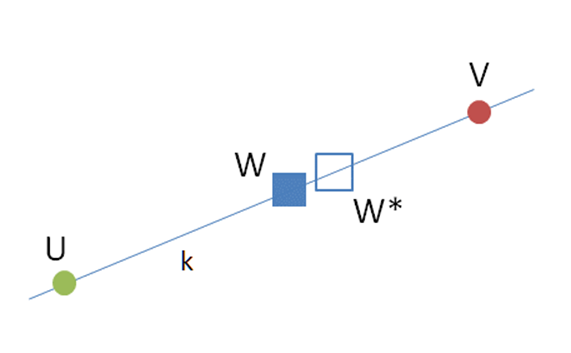
首先,在色度图上选一个待对比的标准颜色W;
然后,在某一个方向上画一条线k,在上面选出两个颜色U和V,这样就可以用适当的方法混合U和V,生成颜色W;
再然后,稍微"干扰"一下U和V的混合条件,改变配比值,从而生成一个和W稍有偏差的新颜色W'(这个偏差方向一定在k线上);
最后,由参与实验的观察者重新调整U和V的混合条件,使得W'回到W上来。而W'其实并不需要和原来的W完全重合,只要是看起来没有色差就行了,所以最后就得到了和W没有色差的W*。
最后的最后,对比一下W和W*的色坐标,就可以知道W附近的颜色宽容度有多大了。
经过这个试验(以及其它的一系列实验),科学家们发现,颜色宽容度并没有一个明确的边界,因为W跟W*的数据是这个样子的:

这是一个假设k线是水平线的示意图。
把W*的x数据画成直方图大概就长这样(其实没有数据,是我随便画的,看个意思):
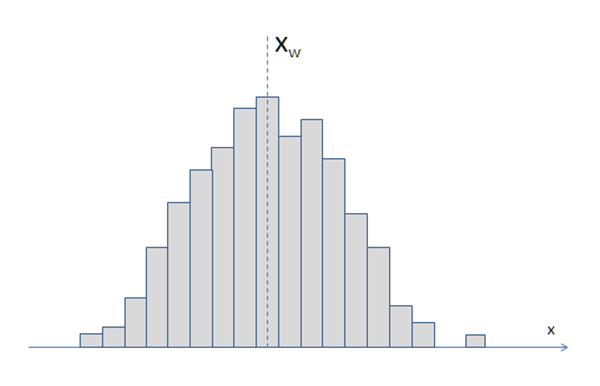
所以,跟我们一般的直觉不同,人眼对色差的判断,有一定的随机性,应该用统计学的眼光来看待这个问题。(怪不得我之前看色差样品的时候老觉得自己眼神不好,为什么色差一会儿有一会儿没有...原来这事儿不能怪我...谁看都一样...
根据正态分布的特点,W*落在三倍标准差以内的概率高达99.7%。也就是说,距离W点三倍标准差以上(三阶麦克亚当圈以外)的点,几乎百分之百会被判定有色差。因此三倍的标准差就被称为恰可察觉差(Just Noticeable Difference,也可译作刚辨差)。
但是!这并不意味着小于恰可察觉差的颜色感觉不到色差!
我们可以说"色坐标一旦超过三阶的圈,一定会有色差",但不能说"没超过三阶的圈就不会有色差"。注意这两者的区别!
当W*的色坐标进入W的三阶圈的范围之内,(被判定为)有色差的概率从99.7%一路下降,直到W*和中心点W重合、概率下降为0为止。
所以,重点就是!即便是色坐标的差值在一个标准差之内,也不一定是没有色差的!虽然概率小,但也不是没有!
因此,在实际应用中,对色差的管控应该具体情况具体分析,根据具体需求来设置一个合理的色差标准(并没有那种放之四海而皆准的阈值来判定有没有色差)。
在麦克亚当的实验中,选择了25个常见的颜色作为待对比的标准颜色。每一个颜色都进行了多个k线方向的测试。而每一个方向,则进行了50次采样,从而计算出标准差,再把这个标准差的大小以线段长度的形式标注在k线上。最后用一个圈把它们连起来,就是一阶的麦克亚当圈。
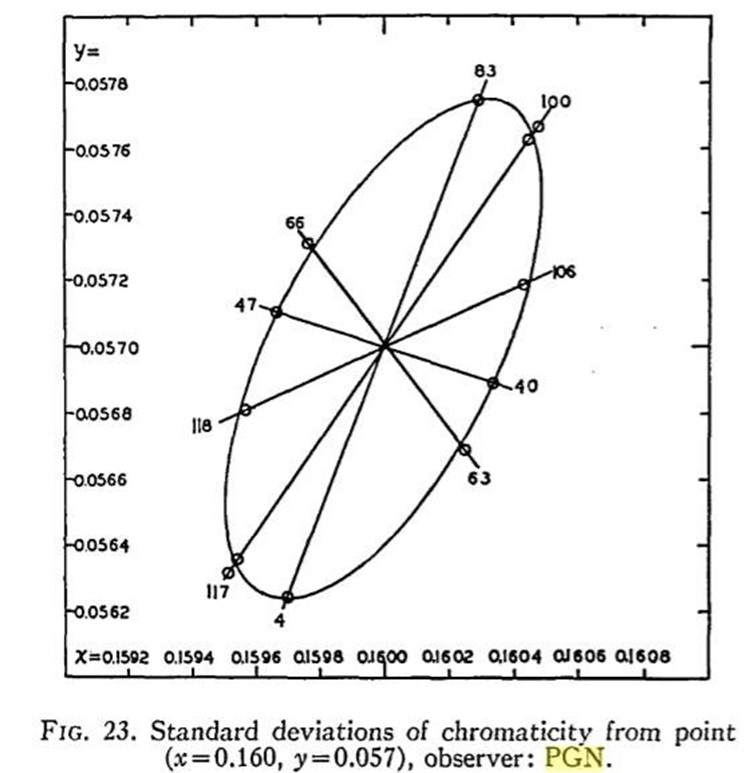
PGN是测试者 Perley G. Nutting 的名字缩写,麦克亚当实验的主要数据都来源于他的观察结果。
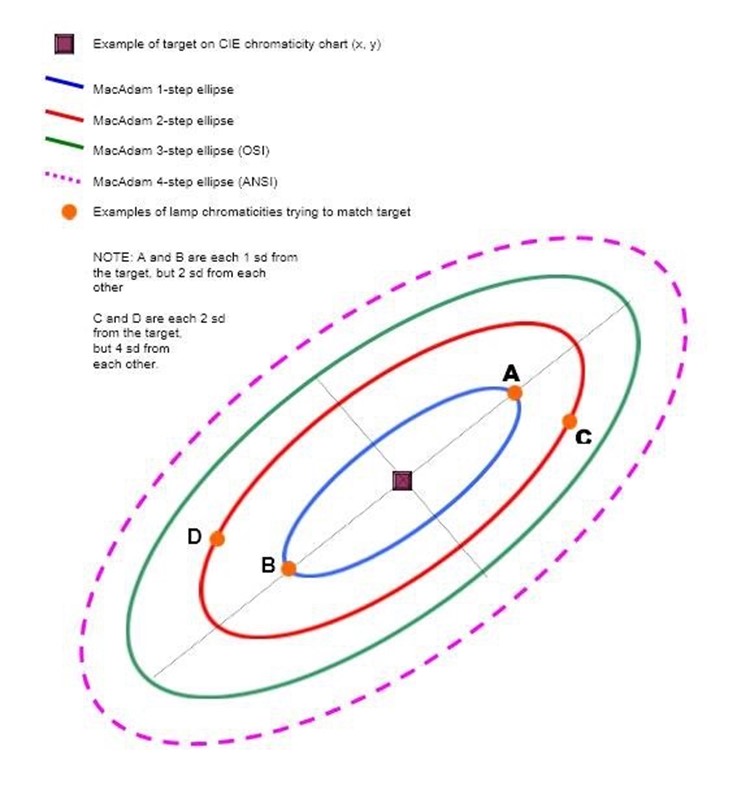
一阶(1-step)对应+/-1 standard deviation(其实一左一右两个方向差了有两个标准差)。
两阶对应正负两个标准差。三阶就对应正负三个标准差。依此类推。
阶数(Step)越大,圈圈也就越大,判定为有色差的概率就越大。
当我们第一眼看到上文中的麦克亚当椭圆示意图的时候,可能会有一种错觉:没有色差的某一个颜色的区域是很大一片。
其实并不!!!
那个图是把一阶麦克亚当椭圆放大了10倍的效果图(也就是五阶)。
放大了10倍!
放大了10倍!
放大了10倍!
重要的事情说三遍!
主要目的就是为了照顾眼神不好的人,啊不,是因为一阶的麦克亚当圈实在太小了,几乎看不出来是个椭圆了,手抖PS一下大概长这样:
采用了错误的P图方案,所以P得花里胡哨的。。。累死了就这样了不要在意这些细节。。。
所以如果不考虑眼神不好的人,大部分人对色差还是非常敏感的!对大多数人而言,在色品图上可以圈出非常非常多种不同的颜色!
从我自己的使用经验上看,也是这样。抬眼一看,色坐标精确到了小数点后第四位,很小嘛!在测量色差的时候,如果两个色坐标相差了0.1,感觉上色差似乎很小的样子。。。其实并不!!!
一阶麦克亚当圈的半径量级大概在0.001上(简化成圆来看)。所以如果两个色坐标之间距离有0.1,按照三阶的刚辨差来算,其实就已经是可识别的色差水平的几十倍了!换句话说,它们之间已经可以容纳下数十种不同的颜色!
So, 我的个人建议,最好把这个色坐标当做千位数来看(就是在头脑里假装不要那个小数点,比如 0.1234 要看作 1234)。色差值在个位数的时候,基本看不出色差。一旦上了十位数,色差很有可能就出来了。
这样做可以让你对色差保持更高的警惕,本人对此可是有过惨痛的教训。。。
LED光源的色差管理
LED光源的色差管理也会用到麦克亚当圈的知识。
之前介绍了,LED出厂的时候,都要按颜色和发光强度来分Bin(分批出货)。而每一个厂家分Bin的方式都是不同的。一般来说,厂家会执行ANSI的标准,按4阶麦克亚当圈来分Bin(ANSI, American National Standards Institute 美国国家标准学会)。
但是我们也看到了,4阶其实范围已经很大了。一些比较牛的厂家就会采用3阶的标准。(也有采用5阶标准的,手动斜眼→_→
虽然各界厂家分Bin的方式各不相同,经常数据一大堆看得你眼花缭乱,但如果你知道他是按几阶麦克亚当圈来分的,你就大概知道它的色差控制水平在哪里 (●ˇ∀ˇ●)

飞利浦某款LED的产品说明书,按3阶麦克亚当圈分Bin。
冷知识
• 人的左眼和右眼对颜色的观察并不同步,双眼同时观察,会给色差判定结果带来波动。所以麦克亚当的实验采用的是单眼测试设备。
一个启发就是,下次判定色差样品的时候不妨闭上一只眼试试。
•
• 亮度的变化会带来色度的变化,所以麦克亚当的实验设计了一个非常复杂的设备,使得在调整色坐标的时候可以自动保持亮度基本不变。
同时,为了避免测试设备带来的系统误差,也颇费了一番功夫。
这个设备长这样o_o:
•
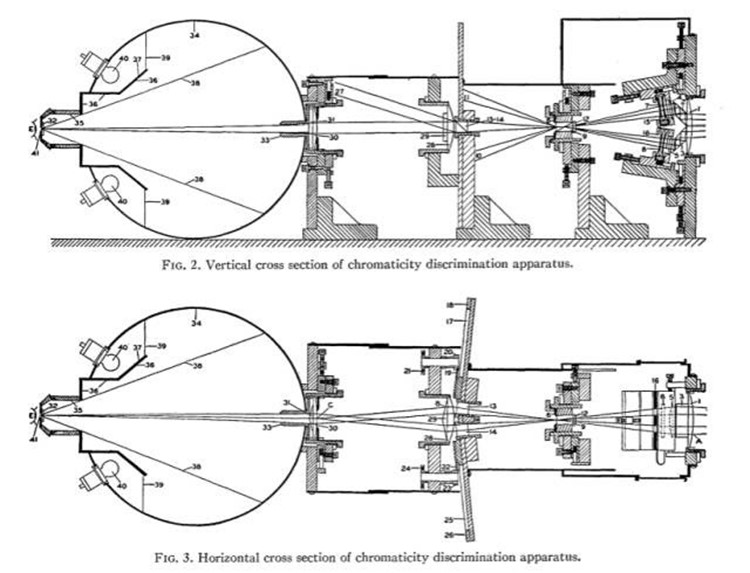
• 让我说点什么好。。。摊手。。。可见柯达当年还是相当牛(有钱)的。。。
• 过去对颜色宽容度的理解,是按"刚辩差"来理解的,也是按这个来研究的。也就是说,大家还以为会有一个明确的阈值来判定色差。结果却发现,这个阈值存在不可避免的波动。
由此才慢慢意识到,应该用统计学的眼光来看待这个问题。
最后,标准差代替了阈值,成为表述颜色宽容度的最佳方案。
(所以下次做色差样品判别的时候,应该多观察几次,多找几个人看看 (´・ω・`)
• 在麦克亚当的实验之前,虽然已经有人认识到,应该用统计学手段来研究颜色宽容度,但都没能拿出真正可靠的数据和结论。因为这需要大样本量的采样测试,数据越多越靠谱。完成这个实验需要调用的时间、资源、耐心和毅力,我光想想都觉得有点吓人。。。
最后,麦克亚当实验的主要测试者Perley G. Nutting 一共进行了约25000次观测。。。
这个数据来之不易,让我们谢谢他~比心♥~
今天就到这里,我们下次再见!