递归算法切记切记退出的条件,比如快速排序中的
if (start >= end)
return;
常见排序算法的复杂度:
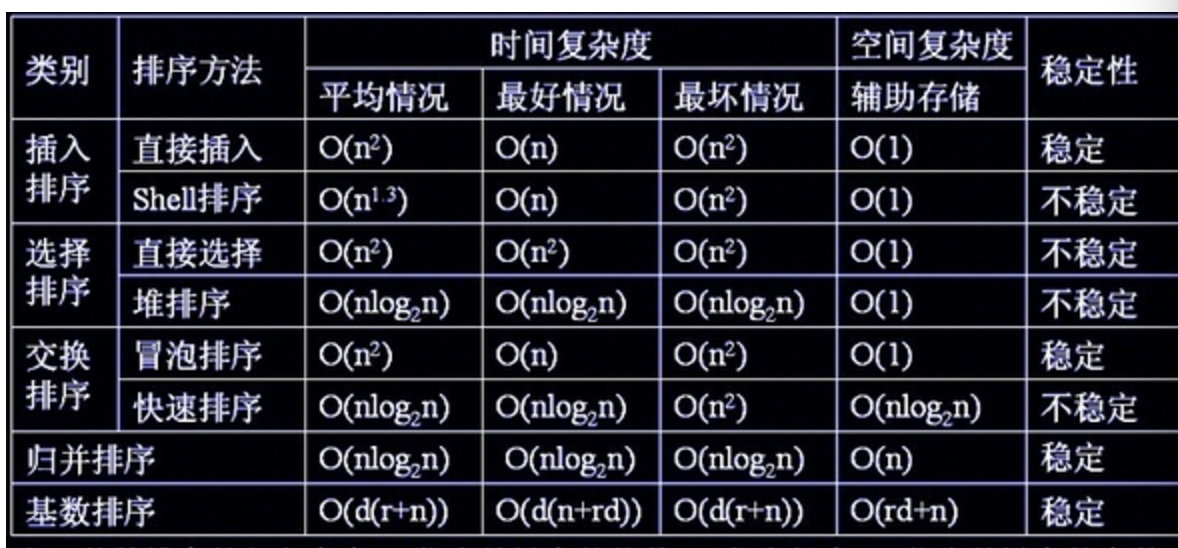
插入排序,实际上是子序列依次向完整序列的增长过程,每次增长主要任务就是为哨兵(新增加的元素)寻找位置!
package com.pt; import static org.junit.Assert.*; import org.junit.Test; public class ArraySort { int[] array = {10,2,4,9,56,5,43,1,65,13,15,9}; //插入排序 @Test public void InsertSort() { int i=1; for (i=1; i < array.length; i++) { int key = array[i]; int j=i; while(j>0&&key<array[j-1]){ array[j]=array[j-1]; j--; } array[j] = key; printArray(array); System.out.println(); } } public void printArray(int[] a){ int i = a.length; while (i>0) { i--; System.out.print(a[i] + ", "); } } }
快速排序:
快速排序的核心思想是分区而治
import static org.junit.Assert.*; import org.junit.Test; public class SortOperator { public void quickSort(int[] inIntegers,int startLoc,int endLoc) { if(startLoc >= endLoc) return; int initStart = startLoc; int initEnd = endLoc; int key = inIntegers[startLoc]; while(startLoc < endLoc){ while(startLoc < endLoc && inIntegers[endLoc] >= key){ endLoc--; } inIntegers[startLoc] = inIntegers[endLoc]; while(startLoc < endLoc && inIntegers[startLoc] <= key){ startLoc++; } inIntegers[endLoc] = inIntegers[startLoc]; } inIntegers[startLoc] = key; quickSort(inIntegers, initStart, startLoc); quickSort(inIntegers, startLoc+1, initEnd); } @Test public void test(){ int[] array = {10,2,4,9,56,5,43,1,65,13,15,99,15}; quickSort(array,0,12); printArray(array); } public void printArray(int[] a){ int i = 0; while (i<a.length) { System.out.print(a[i] + ", "); i++; } } }
归并排序
package com.pt.spring.learn.bean; import java.util.Arrays; public class Sort { public static void main(String[] args) { System.out.println("----start----"); int[] array1 = new int[]{1, 4, 5, 7, 8, 9, 12}; int[] array2 = new int[]{1, 2, 4, 5, 7, 10, 19, 30, 32}; System.out.println(Arrays.toString(binMergeSort(array1, array2))); int[] array = new int[]{1, 3, 2, 4, 8, 6, 5}; sort(array); System.out.println(Arrays.toString(array)); } public static void sort(int[] array) { int[] temp = new int[array.length];//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间 mergeSort(array, 0, array.length - 1, temp); } public static void mergeSort(int[] array, int first, int last, int[] sortArray) { if (first < last) { int mid = (first + last) / 2; mergeSort(array, first, mid, sortArray); mergeSort(array, mid + 1, last, sortArray); mergeSort(array, first, mid, last, sortArray); } } //多路归并排序 public static void mergeSort(int[] arr, int left, int mid, int right, int[] temp) { int i = left; int j = mid + 1; int t = 0; while (i <= mid && j <= right) { if (arr[i] <= arr[j]) { temp[t++] = arr[i++]; } else { temp[t++] = arr[j++]; } } while (i <= mid) { temp[t++] = arr[i++]; } while (j <= right) { temp[t++] = arr[j++]; } t = 0; while (left <= right) { arr[left++] = temp[t++]; } } //二路归并排序 public static int[] binMergeSort(int[] array1, int[] array2) { int i1 = 0; int i2 = 0; int[] ret = new int[array1.length + array2.length]; int i = 0; for (; i1 < array1.length && i2 < array2.length; ) { if (array1[i1] == array2[i2]) { ret[i++] = array1[i1++]; ret[i++] = array1[i2++]; } else if (array1[i1] > array2[i2]) { ret[i++] = array2[i2++]; } else if (array1[i1] < array2[i2]) { ret[i++] = array1[i1++]; } } if (i1 < array1.length) { while (i1 < array1.length) { ret[i++] = array1[i1++]; } } else if (i2 < array2.length) { while (i2 < array2.length) { ret[i++] = array2[i2++]; } } return ret; } }
堆排序:
package com.pt.spring.learn.bean; import java.util.Arrays; /** * 堆,特殊的完全二叉树; * 从0开始计数 * 第i个节点的父节点是(i-1)/2,两个子节点是2i+1和2i+2 * 从1开始计数 * 第i个节点的父节点是i/2,两个子节点是2i和2i+1 */ public class HeapSort { public static void main(String[] args) { int[] array = new int[]{1, 7, 3, 9, 2, 98, 4, 39, 25, 10, 44, 43}; swap(array, 2, 5); System.out.println(Arrays.toString(array)); heapSort(array); System.out.println(Arrays.toString(array)); } public static void heapSort(int[] array) { for (int i = array.length; i > 0; i--) { makeHeap(array, i); swap(array, 0, i - 1); } } /*** * 调整array 使得前n个元素构成大顶堆(从1开始计数) * 借助adjustHeap方法,自下而上调整,自右向左 * @param array * @param n */ public static void makeHeap(int[] array, int n) { for (int i = n / 2 - 1; i >= 0; i--) { adjustHeap(array, i, n); } } /** * 调整第i个节点及其子节点,使得以i为根节点的树是一个大顶堆
* 但对于堆排序来说,只需要使得第i个节点的位置是最大值(或最小值)即可,所以如果仅用于排序,此函数还有优化空间
* len的作用是只关注前len个元素 * * @param array * @param i * @param len */ public static void adjustHeap(int[] array, int i, int len) { int maxChild = i * 2 + 1;//假设左节点是父子中值最大的 while (maxChild < len) { //首先取出两个子节点最大的节点 if (maxChild + 1 < len && array[maxChild + 1] > array[maxChild]) { maxChild++; } //比较最大子节点与父节点的大小 if (array[i] > array[maxChild]) { break; } else { swap(array, i, maxChild); i = maxChild; maxChild = i * 2 + 1; } } } public static void swap(int[] array, int i, int j) { int temp = array[i]; array[i] = array[j]; array[j] = temp; } }