链接:https://www.nowcoder.com/acm/contest/148/D
来源:牛客网
Prefix Sum is a useful trick in data structure problems.
For example, given an array A of length n and m queries. Each query gives an interval [l,r] and you need to calculate . How to solve this problem in O(n+m)? We can calculate the prefix sum array B in which Bi is equal to
. How to solve this problem in O(n+m)? We can calculate the prefix sum array B in which Bi is equal to  . And for each query, the answer is Br-Bl-1.
. And for each query, the answer is Br-Bl-1.
Since Rikka is interested in this powerful trick, she sets a simple task about Prefix Sum for you:
Given two integers n,m, Rikka constructs an array A of length n which is initialized by Ai = 0. And then she makes m operations on it.
There are three types of operations:
1. 1 L R w, for each index i ∈ [L,R], change Ai to Ai + w.
2. 2, change A to its prefix sum array. i.e., let A' be a back-up of A, for each i ∈ [1,n], change Ai to .
3. 3 L R, query for the interval sum .
.
For example, given an array A of length n and m queries. Each query gives an interval [l,r] and you need to calculate
Since Rikka is interested in this powerful trick, she sets a simple task about Prefix Sum for you:
Given two integers n,m, Rikka constructs an array A of length n which is initialized by Ai = 0. And then she makes m operations on it.
There are three types of operations:
1. 1 L R w, for each index i ∈ [L,R], change Ai to Ai + w.
2. 2, change A to its prefix sum array. i.e., let A' be a back-up of A, for each i ∈ [1,n], change Ai to .
3. 3 L R, query for the interval sum
输入描述:
The first line contains a single number t(1≤ t ≤ 3), the number of the testcases.
For each testcase, the first line contains two integers n,m(1 ≤ n,m ≤ 10
5
).
And then m lines follow, each line describes an operation(1 ≤ L ≤ R≤ n, 0 ≤ w ≤ 10
9
).
The input guarantees that for each testcase, there are at most 500 operations of type 3.
输出描述:
For each query, output a single line with a single integer, the answer modulo 998244353.
示例1
输入
1 100000 7 1 1 3 1 2 3 2333 6666 2 3 2333 6666 2 3 2333 6666
输出
13002 58489497 12043005
操作有两种,1操作是给l-r区间内的数都加w,2操作是让这个数列变为它的前缀和序列 我们知道,2操作之后得到的新的序列差分之后就是操作前的序列,所以如果只有2操作的话,就是给你一个差分了很多次之后的序列求原序列 但是它还有1操作,1操作对于差分的级别没有变化,但我们知道在原来的序列的l-r区间+w,其实就是在它的差分序列l处+w,r+1处-w 那么现在的问题就在于在这样的一个差分序列的表格中,如果我们在某个点+w,造成的影响是什么

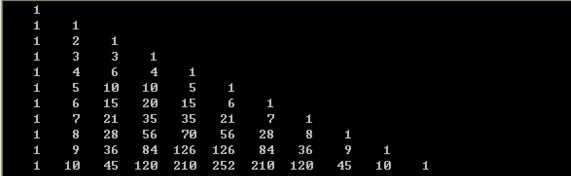
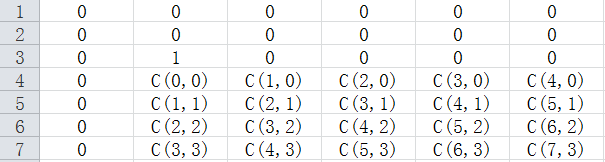
我们发现在一个点+w之后,影响的是它右下角的所有点,每个行的系数是杨辉三角的一列,所以如果在(i,j)点+w,那么(x,y)点的系数为C(x-ai+y-j-1,x-i-1) 然后3操作不超过500次,所以我们就记录下每次操作,然后对每次询问O(n)计算即可

#include<bits/stdc++.h> #define ll long long using namespace std; const int p=998244353; const int N=2e5+10; int n,m,T,op,l,r,w,cnt; struct orz{ int x,pos,w; }a[N]; ll fac[N],inv[N]; ll poww(ll x,int y) { x%=p; ll ret=1; while (y) { if (y&1) ret=ret*x%p; x=x*x%p; y>>=1; } return ret; } void pre() { fac[0]=1; for (int i=1;i<N;i++) fac[i]=fac[i-1]*i%p; inv[N-1]=poww(fac[N-1],p-2); for (int i=N-2;i>=0;i--) inv[i]=inv[i+1]*(i+1)%p; } ll C(int a,int b) { if (b>a||b<0) return 0; return fac[a]*inv[b]%p*inv[a-b]%p; } ll solve(int x,int y) { ll ret=0; for (int i=1;i<=cnt;i++) { if (a[i].x<=x&&a[i].pos<=y) ret=(ret+C(x-a[i].x+y-a[i].pos-1,x-a[i].x-1)*(ll)a[i].w%p)%p; } return ret; } int main() { scanf("%d",&T); pre(); while (T--) { scanf("%d%d",&n,&m); int now=1; cnt=0; while (m--) { scanf("%d",&op); if (op==1) { scanf("%d%d%d",&l,&r,&w); cnt++; a[cnt].x=now-1; a[cnt].pos=l; a[cnt].w=w%p; cnt++; a[cnt].x=now-1; a[cnt].pos=r+1; a[cnt].w=-w%p; } else if (op==2) now++; else { scanf("%d%d",&l,&r); ll ans=((solve(now+1,r)-solve(now+1,l-1))%p+p)%p; printf("%lld ",ans); } } } return 0; }
