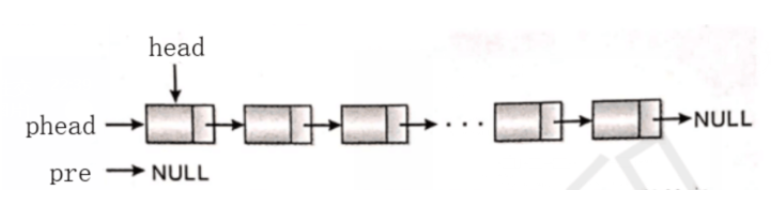
1、反转链表
link InvertList(link head){
link pre,phead,temp;
phead = head; //将phead指向链表头,做游标使用
pre = NULL; //pre为头指针之前的节点
while(phead != NULL){
temp = pre;
pre = phead;
phead = phead->next;
pre->next = temp; //pre接到之前的节点
}
return pre;
}
2、找出数组中连续子序列之和最大的子序列数组,并输出起止位置索引
方法:
public void maxSum(int[] nums) {
int start = 0;
int end = 0;
int max = 0;
int temp = 0;
int ts = 0;
for(int i = 0; i < nums.length; i++) {
temp += nums[i];
if(temp < 0) {
ts = i + 1;
temp = 0;
} else {
if(temp > max) {
start = ts;
end = i;
max = temp;
}
}
}
System.out.println("maxSum = " + max + ", start : " + start + ", end = " + end);
}
先给定一个temp,让它从头开始加每个数字,temp小于0时,我们重新开始计算,另temp = 0,让开始的下标从这个位置开始。再记一个max,是我们用来存结果的,如果temp大于max,则让max = temp,让end下标移到这个位置.
时间复杂度O(N)
3、用JAVA模拟死锁
死锁是在多线程情况下最严重的问题,在多线程对公共资源(文件,数据)等进行操作时,彼此不释放自己的资源,而去试图操作其他线程的资源,而形成的交叉引用,就会产生死锁。
假如我有一个需求,有一个线程,先写入A文件,在顺序写入B文件,再保存起来。还有另一个线程,先写入B文件,再顺序写入A文件,再保存起来。代码如下:
private static String fileA = "A文件";
private static String filedB = "B文件";
public static void main(String[] args) {
new Thread() { //线程1
//重写run方法
public void run() {
while (true) {
synchronized (fileA) {//打开文件A,线程独占fileA
System.out.println(this.getName() + ":文件A写入");
synchronized (filedB) {
System.out.println(this.getName() + ":文件B写入");
}
System.out.println(this.getName() + ":所有文件保存");
}
}
}
}.start();
new Thread() { //线程2
//重写run方法
public void run() {
while (true) {
synchronized (filedB) {//打开文件B,线程独占filedB
System.out.println(this.getName() + ":文件B写入");
synchronized (fileA) {
System.out.println(this.getName() + ":文件A写入");
}
System.out.println(this.getName() + ":所有文件保存");
}
}
}
}.start();
}
4、B树和B+树的区别
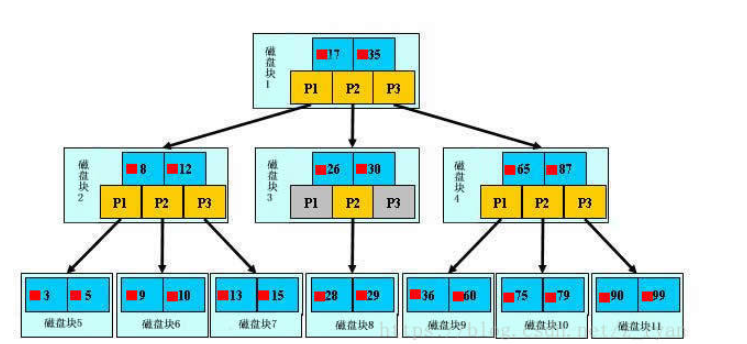
B树
一个m阶的B树具有如下几个特征:B树中所有结点的孩子结点最大值称为B树的阶,通常用m表示。一个结点有k个孩子时,必有k-1个关键字才能将子树中所有关键字划分为k个子集。
1.根结点至少有两个子女。
2.每个中间节点都包含k-1个元素和k个孩子,其中 ceil(m/2) ≤ k ≤ m
3.每一个叶子节点都包含k-1个元素,其中 ceil(m/2) ≤ k ≤ m
4.所有的叶子结点都位于同一层。
5.每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域划分
6.每个结点的结构为:(n,A0,K1,A1,K2,A2,… ,Kn,An)
其中,Ki(1≤i≤n)为关键字,且Ki<Ki+1(1≤i≤n-1)。
Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。
n为结点中关键字的个数,满足ceil(m/2)-1≤n≤m-1。
————————————————
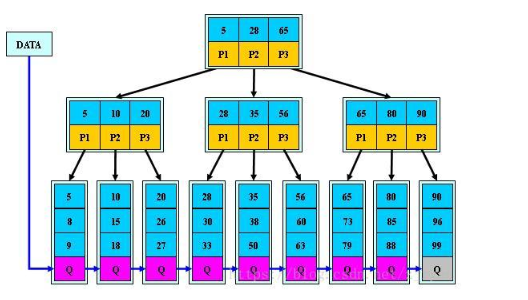
B+树
1.有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据 都保存在叶子节点。 2.所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小 自小而大顺序链接。 3.所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。
5、Linux下的top命令
top命令是Linux下常用的性能分析工具,能够实时显示系统中各个进程的资源占用状况,类似于Windows的任务管理器
PID — 进程id USER — 进程所有者 PR — 进程优先级 NI — nice值。负值表示高优先级,正值表示低优先级 VIRT — 进程使用的虚拟内存总量,单位kb。VIRT=SWAP+RES RES — 进程使用的、未被换出的物理内存大小,单位kb。RES=CODE+DATA SHR — 共享内存大小,单位kb S —进程状态。D=不可中断的睡眠状态 R=运行 S=睡眠 T=跟踪/停止 Z=僵尸进程 %CPU — 上次更新到现在的CPU时间占用百分比 %MEM — 进程使用的物理内存百分比 TIME+ — 进程使用的CPU时间总计,单位1/100秒 COMMAND — 进程名称(命令名/命令行)
ps -ef kill pid
6、最长不下降子序列-复杂度为O(nlogn)

实现方法就是新开一个数组 dd ,用它来记录每个序列的末尾元素,以求最长不下降为例,d[k]d[k] 表示长度为k的不下降子序列的最小末尾元素。
7、扔鸡蛋问题
假如有100层楼,总共有2个鸡蛋。需要多少次才能试探出临界点,比如,在第三层扔下去,不碎;在第四层扔下去,碎了,那第三层和第四层就是临界点。
如果之前没准备过的话,大概第一个想到的就是二分法。
1. 二分法
首先在第50层丢第一个鸡蛋,若鸡蛋碎了,则在第一层开始往上丢鸡蛋,最坏情况是试探49+1次,为什么要从第一层开始尝试呢,因为只有2个鸡蛋;若鸡蛋没碎,则在75层丢第二次,若碎了则在(50,75)区间从下往上尝试。。。
结论:二分法最坏尝试次数是50次。
显然二分法不是一个好的解决方案,这里介绍第二种方法“平方根法”。
2. 平方根法
因为100是10的平方,我们可以把10作为一个区间去尝试,即第一层在第10层丢,不碎,则去第20层丢。。。,一直到第90层丢,还不碎的话,则在(91,100]层逐一尝试,最坏情况是9+10=19次,19次了,比二分法要前进了一半以上了。并且平方根法还可以再优化一下:以15层作为起点,步伐是10。即第一层是15,第二次是25,第三次是35,45…95。这种优化后的呢,最坏情况下,是在第9次(第95层碎),然后在(85,95)区间尝试9次,即优化后的最坏尝试次数是9+9=18次。
结论:平方根法最坏情况下是19次,平方根优化法最坏情况下是18次。
8、深度学习训练中梯度消失的原因有哪些?有哪些解决方法?
网友回答:
- 在深层网络中,使用了sigmod函数;
- 将sigmod函数更换为Relu或者LeakRelu函数;
- fune-tunning进行微调;
- 使用残差结构;
- 使用BN。
梯度消失产生的主要原因有:一是使用了深层网络,二是采用了不合适的损失函数。
(1)目前优化神经网络的方法都是基于BP,即根据损失函数计算的误差通过梯度反向传播的方式,指导深度网络权值的更新优化。其中将误差从末层往前传递的过程需要链式法则(Chain Rule)的帮助。而链式法则是一个连乘的形式,所以当层数越深的时候,梯度将以指数形式传播。梯度消失问题一般随着网络层数的增加会变得越来越明显。在根据损失函数计算的误差通过梯度反向传播的方式对深度网络权值进行更新时,得到的梯度值接近0,也就是梯度消失。
(2)计算权值更新信息的时候需要计算前层偏导信息,因此如果激活函数选择不合适,比如使用sigmoid,梯度消失就会很明显,原因如果使用sigmoid作为损失函数,其梯度是不可能超过0.25的,这样经过链式求导之后,很容易发生梯度消失。
解决方法:
(1)pre-training+fine-tunning
此方法来自Hinton在2006年发表的一篇论文,Hinton为了解决梯度的问题,提出采取无监督逐层训练方法,其基本思想是每次训练一层隐节点,训练时将上一层隐节点的输出作为输入,而本层隐节点的输出作为下一层隐节点的输入,此过程就是逐层“预训练”(pre-training);在预训练完成后,再对整个网络进行“微调”(fine-tunning)。此思想相当于是先寻找局部最优,然后整合起来寻找全局最优,此方法有一定的好处,但是目前应用的不是很多了。
(2) 选择relu等梯度大部分落在常数上的激活函数
relu函数的导数在正数部分是恒等于1的,因此在深层网络中使用relu激活函数就不会导致梯度消失的问题。
(3)batch normalization
BN就是通过对每一层的输出规范为均值和方差一致的方法,消除了权重参数放大缩小带来的影响,进而解决梯度消失的问题,或者可以理解为BN将输出从饱和区拉到了非饱和区。
(4) 残差网络的捷径(shortcut)
相比较于之前的网络结构,残差网络中有很多跨层连接结构(shortcut),这样的结构在反向传播时多了反向传播的路径,可以一定程度上解决梯度消失的问题。
(5)LSTM的“门(gate)”结构
LSTM全称是长短期记忆网络(long-short term memory networks),LSTM的结构设计可以改善RNN中的梯度消失的问题。主要原因在于LSTM内部复杂的“门”(gates),LSTM通过它内部的“门”可以在更新的时候“记住”前几次训练的”残留记忆“。
9、过拟合的解决
- 增强训练样本集;
- 增加样本集的维度;
- 如果模型复杂度太高,和训练样本集的数量级不匹配,此时需要降低模型复杂度;
- 正则化,尽可能减少参数;
- 添加Dropout