插空变距离问题

插空不变距离问题

枚举法:

分配法的规则:
(先假定随便给5台给三个人中的一个人C31,然后再把最后的五台分配给三个人,这样其中一个人就会>5

【被坑过的套路】:
1、第2/3/4/5层的差值是有规律的---奇偶
2、相邻两项的和、差、乘积 -- 有规律的【1+2 = 3+4】
3、都是n的乘积【n^2】
4、所求项各位数字之和应为10
5、多重数列、、
【原数列为多重数列。
奇数项:2、7、19、45、(99),无明显规律,作差: 5、12、26、(54)为二倍递推修正数列,具体如下:,
,
,修正项为2;
偶数项:3、10、26、60,无明显规律,作差: 7、16、34为二倍递推修正数列,具体如下:,
,修正项为2;】
重复做某事的解法(这些人都做了这个事)
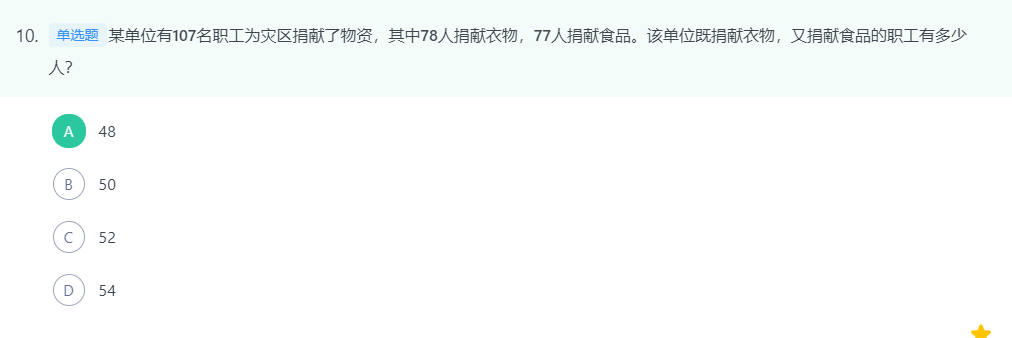
据两集合容斥原理问题的公式:,可以得到
。
,尾数为8,只有A项符合。
最值问题(这些人未必都做了这个事)


间隔问题:
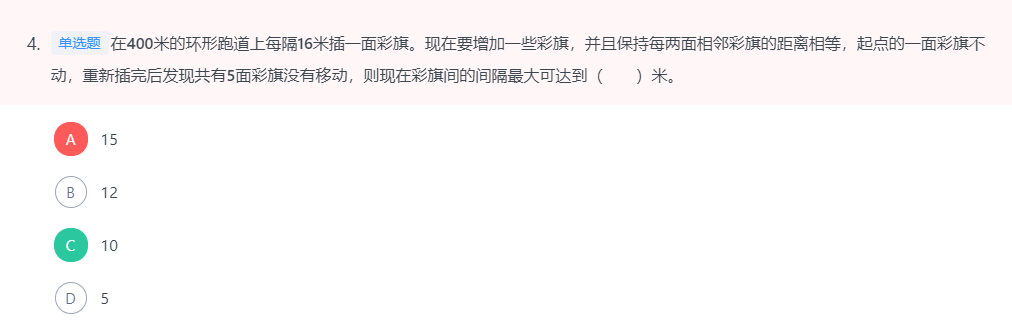
原来一共插了400÷16=25面旗。题中5面彩旗没动,一共分隔出5段跑道,每段400÷5=80米。在被分隔出的80米内,原来是16米一个小段,现在被修改成另外一个长度x。两种情况下,前后两端的彩旗都没动,中间全部被移动,那代表x与16的最小公倍数为80。代入选项,C、D两项都符合要求,但题目求最大值,则选C。
故正确答案为C。
共同工作问题:
一批零件若交由赵师傅单独加工,需要10天完成;若交由孙师傅单独加工,需要15天完成。两位师傅一起加工这批零件,需要( ) 天完成。
已知完成工程的时间,赋值给工作总量。设工程总量为30,则赵师傅的效率为30÷10=3,孙师傅的效率为30÷15=2,因此两位师傅合作需要。
故正确答案为B。
三集合容斥原理:

设参加该次活动的总人数为x人,根据三集合容斥原理非标准型公式可得:189+152+135-130-2×69=x-44,计算尾数,x的尾数为2。
故正确答案为B。
合作加工问题

由条件,“乙需要超过计划时间5天完成,两厂合作加工3天后由乙厂加工也可在计划时间完成”,则可推知乙5天完成的工作量等于甲3天完成的工作量,即,
。设加工这批零件计划时间是
天,根据工程总量相等可得:
,解得
。
故正确答案为C。
ps: 这里推测出甲乙的工作效率比较很重要!
工程问题——第一、二、三类赋值
(关键在设: 工作总量=工作效率×工作时间)
(工作总量记得设成公倍数的方式,尽量不要设成1)
【例1】一项工程,甲、乙合作12天完成,乙、丙合作9天,丙、丁合作12天完成。如果甲、丁合作,则完成这项工程需要的天数是:
A.16
B.18
C.24
D.26

【例2】某项工程,甲工程队单独施工需要30天完成,乙施工队单独施工需要25天完成,甲队单独施工了4天后改由两队一起施工,期间甲队休息了若干天,最后整个工程共耗时19天完成,问甲队中途休息了几天?
A.1
B.3
C.5
D.7

(这里中途撤离不知道多少天,但是可以确定乙工作了19-4天)
【例3】单独完成某项工作,甲需要16小时,乙需要12小时。如果按照甲、乙、甲、乙、……的顺序轮流工作,每次1小时,那么完成这项工作需要多长时间?( )
A.13小时40分钟
B.13小时45分钟
C.13小时50分钟
D.14小时

(照样是这么设,但是这里甲+乙是一个周期-2小时)
【作业A1】若将一项工程的1/6、1/4、1/3和1/4依次分配给甲、乙、丙、丁四家工程队,分别需要15天、15天、30天和9天完成,则他们合作完成该项工程需要的时间是( )。
A.12天
B.15天
C.18天
D.20天

【作业B1】工厂有5条效率不同的生产线。某个生产项目如果任选3条生产线一起加工,最快需要6天整,最慢需要12天整;5条生产线一起加工,则需要5天整。问如果所有生产线的产能都扩大一倍,任选2条生产线一起加工最多需要多少天完成?( )
A.11
B.13
C.15
D.30

(这里是假设生产线12345,题目的意思是找最多天数-4+5,因此用项之间相消可以得出结果)
(注意产能扩大一倍,就是说第二项那里的效率都乘2)
【作业B2】某商铺甲乙两组员工利用包装礼品的边角料制作一批花朵装饰门店。甲组单独制作需要10小时,乙组单独制作需要15小时,现两组一起做,期间乙组休息了1小时40分,完成时甲组比乙组多做300朵。问这批花有多少朵?( )
A.600
B.900
C.1350
D.1500

(注意:这里的30是虚拟的工作总量,算出来的t是真实的工作时间,也就是 甲:5+5/3,乙:5)
(在这个时间段内乙做了2*5=10的虚拟工作总量,甲做了30-10=20的虚拟)
(题目显示说甲比乙真实的差了300),因此就有10/300(真实相差) = 30/真实总量
【例2】A工程队的效率是B工程队的2倍,某工程交给两队共同完成需要6天。如果两队的工作效率均提高一倍,且B队中途休息了1天,问要保证工程按原来的时间完成,A队中途最多可以休息几天?( )
A.4
B.3
C.2
D.1

【例3】甲、乙、丙3个施工队,乙的工效与甲、丙两队合作的工效相等,丙的工效是甲、乙两队合作工效的四分之一。现有一项工程,据测算,三队合作30个工作日可完成。如果由甲队单独来做,需要多少个工作日?( )
A.60
B.96
C.100
D.150

(这个题关键是根据题目的两个等式、找出甲乙丙三个人的工作效率比例)
【作业B1】小张和小赵从事同样的工作,小张的效率是小赵的1.5倍。某日小张工作几小时后小赵开始工作,小赵工作了1小时之后,小张已完成的工作量正好是小赵的9倍。再过几个小时,小张已完成的工作量正好是小赵的4倍?( )
A.1
B.1.5
C.2
D.3

【作业C】甲、乙、丙三个工厂承接A和B两批完全相同的加工订单,如果甲厂和乙厂负责A订单而丙厂负责B订单,则丙厂要比甲厂和乙厂晚15天完成;如在上述条件下甲厂分配1/3的生产资源或者乙厂分配1/5的生产资源用于B订单的生产,则A、B两个订单同时完成。问如果合并三个工厂的生产能力,第几天可以完成A订单的生产任务?( )
A.22
B.24
C.25
D.26
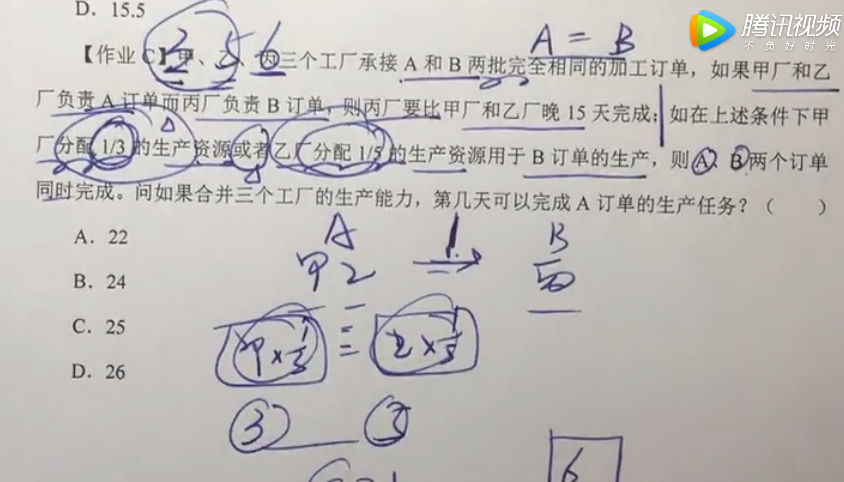
(注意:这里是先找到甲乙的工作效率比例: 3:5)
然后再由于无论是甲/乙给1,都能和A一样完成B任务,所以知道丙的工作效率是6.因此三者比例是3:5:6
由于题目知道: (3+5)*t = 6*(t+15) 可以得出
n个工人的工程问题
(就是把工人的工作效率设置为1,就可以计算了)
【例1】建筑公司安排100名工人去修某条路,工作2天后抽调走30名工人,又工作了5天后再抽调走20名工人,总共用时12天修完。如整条路希望在10天内修完,且中途不得增减人手,则要安排多少名工人?( )
A.80
B.90
C.100
D.120

【例2】某农场有36台收割机,要收割完所有的麦子需要14天时间。现收割了7天后增加4台收割机,并通过技术改造使每台机器的效率提升5%,问收割完所有的麦子还需要几天?( )
A.3
B.4
C.5
D.6

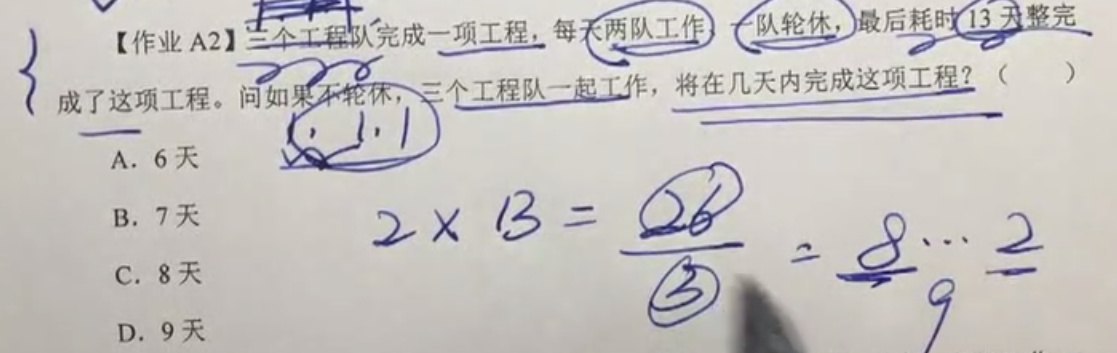
【作业A2】三个工程队完成一项工程,每天两队工作、一队轮休,最后耗时13天整完成了这项工程。问如果不轮休,三个工程队一起工作,将在几天内完成这项工程?( )
A.6天
B.7天
C.8天
D.9天
【作业B1】工程队接到一项工程,投入80台挖掘机。如连续工作30天,每天工作10小时,正好按期完成。但施工过程中遭遇大暴雨,有10天时间无法施工。工期还剩8天时,工程队增派70台挖掘机并加班施工。问工程队若想按期完成,平均每天需多工作多少个小时?( )
A.1.5
B.2
C.2.5
D.3

【作业B2】某工厂与订货商签订合同,约定订货商在订单生产完成50%和80%的时候分别支付两笔货款。在派6名工人生产4天后,完成了订单的8%。如增派9名工人加入生产,则订货商在支付第一笔和第二笔货款间的时间间隔为多少天?(假定所有工人工作效率相同)( )
A.6
B.10
C.12
D.15

(注意:这里问的是第一和第二的间隔,这个区间的时候已经是15人在干活了,我们就不用考虑之前增派人数的时间变化问题)
最值问题①(至少+保证)
笔记整理:
最不利构造
题干特征:至少+保证
解题思路:
①找到保证要完成什么事,目标:把他气死
②“气死”之后+1即为答案
至于怎么“气死”:
1.想要什么别给什么;
2想要N,先给(达到)N-1;
3.不需要的东西统统都给。
【例1】一个袋内有100个球,其中有红球28个、绿球20个、黄球12个、蓝球20个、白球10个、黑球10个。现在从袋中任意摸球出来,如果要使摸出的球中,至少有15个球的颜色相同,问至少要摸出几个球才能保证满足上述要求?( )
A.78个
B.77个
C.75个
D.68个

【例3】某单位组织党员参加党史、党风廉政建设、科学发展观和业务能力四项培训,要求每名党员参加且只参加其中的两项。无论如何安排,都有至少5名党员参加的培训完全相同。问该单位至少有多少名党员?( )
A.17
B.21
C.25
D.29

【作业A2】在2011年世界产权组织公布的公司全球专利申请排名中,中国中兴公司提交了2826项专利申请,日本松下公司申请了2463项,中国华为公司申请了1831项,分别排名前3位,从这三个公司申请的专利中至少拿出多少项专利,才能保证拿出的专利一定有2110项是同一公司申请的专利?( )
A.6049
B.6050
C.6327
D.6328

(典型的想要什么先不给,先给其他的给满了,再+1)
【作业B1】某个社区老年协会的会员都在象棋、围棋、太极拳、交谊舞和乐器五个兴趣班中报名了至少一项。如果要在老年协会中随机抽取会员进行调查,至少要调查多少个样本才能保证样本中有4名会员报的兴趣班完全相同?( )
A.93
B.94
C.96
D.97

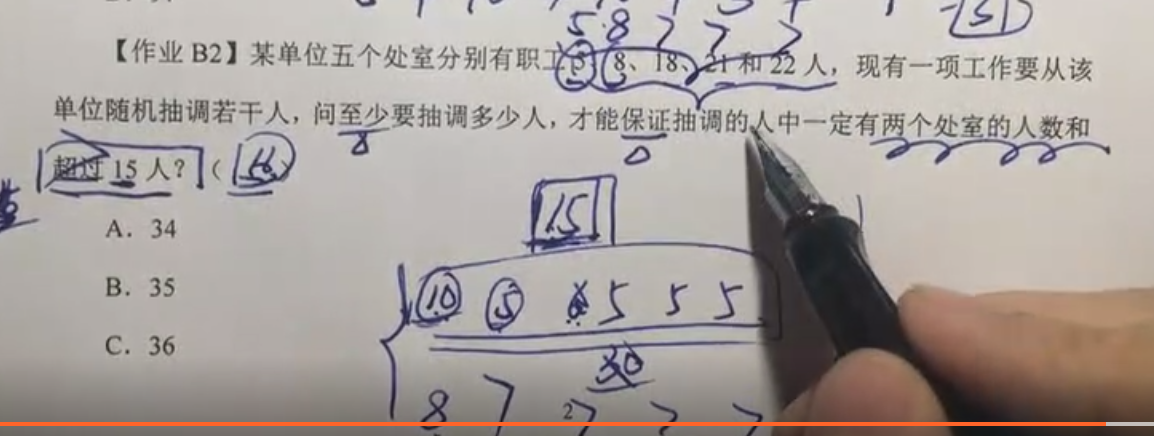
【作业B2】某单位五个处室分别有职工5、8、18、21和22人,现有一项工作要从该单位随机抽调若干人,问至少要抽调多少人,才能保证抽调的人中一定有两个处室的人数和超过15人?( )
A.34
B.35
C.36
D.37
最值问题②(构造数列)
笔记整理:
题型识别:
N件物品分成M项,求其中某一项的最值(最大值或最小值)。
解题思路:
①编号:分成几项即依次编号为①②③④……
②求谁设谁
③按照题目要求完成构造、利用总和为定值列方程求解
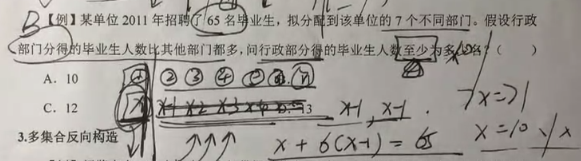
【例3】某单位2011年招聘了65名毕业生,拟分配到该单位的7个不同部门。假设行政部门分得的毕业生人数比其他部门都多,问行政部分得的毕业生人数至少为多少名?( )
A.10
B.11
C.12
D.13
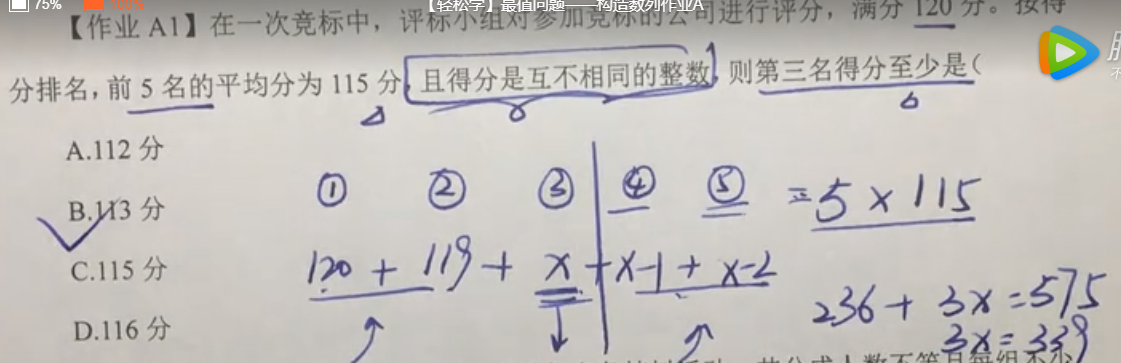
作业A1】在一次竞标中,评标小组对参加竞标的公司进行评分,满分120分。按得分排名,前5名的平均分为115分,且得分是互不相同的整数,则第三名得分至少是( )。
A.112分
B.113分
C.115分
D.116分
【作业B2】有100人参加五项活动,参加人数最多的活动的人数不超过参加人数最少的活动人数的两倍,问参加人数最少的活动最少有多少人参加?( )
A.10
B.11
C.12
D.13

最值问题③(多集合反向构造)
多集合问题:(反向、求和、做差)
解题思路:反向、求和、做差。(-、+、-)
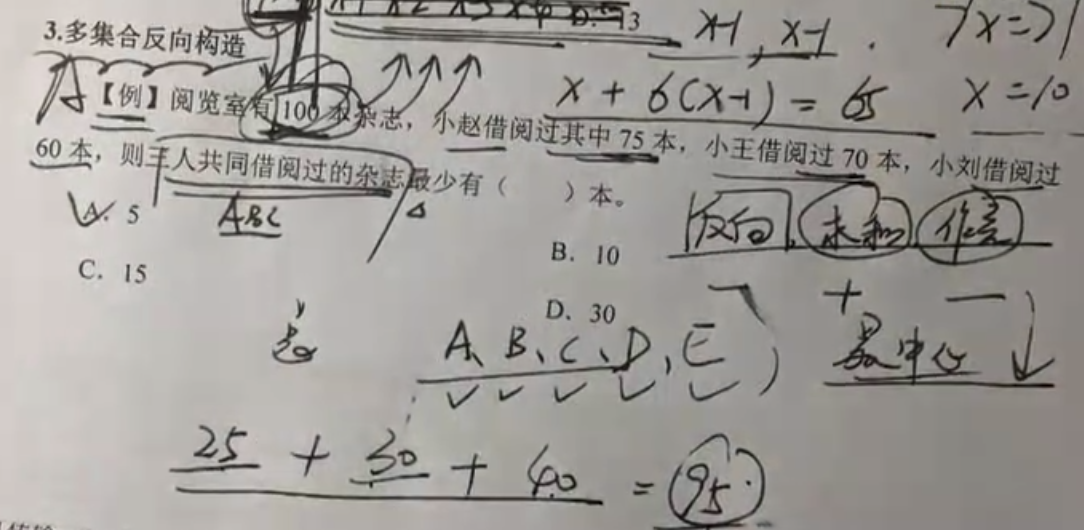
【作业B1】共有100个人参加某公司的招聘考试,考试的内容共有5道题,1~5题分别有80人、92人、86人、78人和74人答对。答对3道和3道以上的人员能通过考试,请问至少有多少人能通过这次考试?( )
A.30
B.55
C.70
D.74
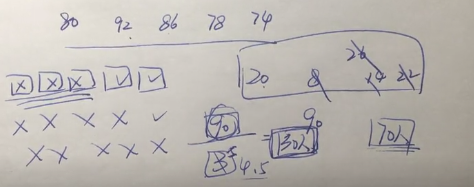
(这个题其实就是求最多不能通过的人数,由题目退出一共有90个题没人答对,那么如果人均错三个,那不通过的人是最多的.)
(所以用90/3,错哪个题其实无所谓的)
【作业B2】书法大赛的观众对5幅作品进行不记名投票。每张选票都可以选择5幅作品中的任意一幅或多幅,但只有在选择不超过2幅作品时才为有效票。5幅作品的得票数(不考虑是否有效)分别为总票数的69%、63%、44%、58%和56%。问本次投票的有效率最高可能为多少?( )
A.65%
B.70%
C.75%
D.80%

集合容斥——两集合、三集合基本公式型
两集合标准公式:总数-两者都不=A+B-AB
三集合标准公式:总数-三者都不=A+B+C-AB-AC-BC+ABC
三集合变形公式:总数-三者都不=A+B+C-同时两者-2ABC
什么时候需要画图:出现“只”满足某一个
如何画图标数:从中心向外侧
(同时满足两者的情况)
【作业A2】运动会上100名运动员排成一列,从左向右依次编号为1-100,选出编号为3的倍数的运动员参加开幕式队列,而编号为5的倍数的运动员参加闭幕式队列。问既不参加开幕式又不参加闭幕式队列的运动员有多少人?( )
A.46
B.47
C.53
D.54

【作业B1】一旅行团共有50位游客到某地旅游,去A景点的游客有35位,去B景点的游客有32位,去C景点的游客有27位,去A、B景点的游客有20位,去B、C景点的游客有15位,三个景点都去的游客有8位,有2位游客去完一个景点后先行离团,还有1位游客三个景点都没去。那么,50位游客中有多少位恰好去了两个景点?( )
A.29
B.31
C.35
D.37

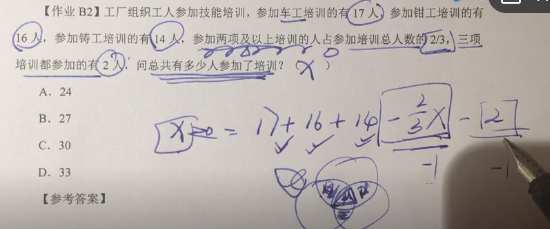
【作业B2】工厂组织工人参加技能培训,参加车工培训的有17人,参加钳工培训的有16人,参加铸工培训的有14人,参加两项及以上培训的人占参加培训总人数的2/3,三项培训都参加的有2人,问总共有多少人参加了培训?( )
A.24
B.27
C.30
D.33
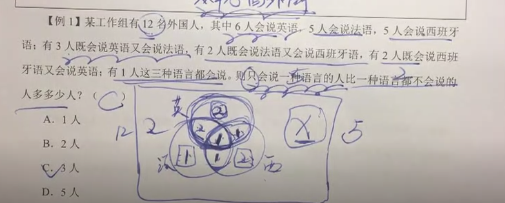
【例1】某工作组有12名外国人,其中6人会说英语,5人会说法语,5人会说西班牙语;有3人既会说英语又会说法语,有2人既会说法语又会说西班牙语,有2人既会说西班牙语又会说英语;有1人这三种语言都会说。则只会说一种语言的人比一种语言都不会说的人多多少人?( )
A.1人
B.2人
C.3人
D.5人
(年份能够被4整除,就是366天,闰年)
(但是整100的年份,例如2100,2000,就要用400去除,才能看出)
【例3】2010年2月15日后第80天的日期是( )。
A.5月5日
B.5月6日
C.5月3日
D.5月4日

如果是计算星期几的问题:
(计算天数,所有的天数加起来除7,得到的余数,然后星期n+余数)
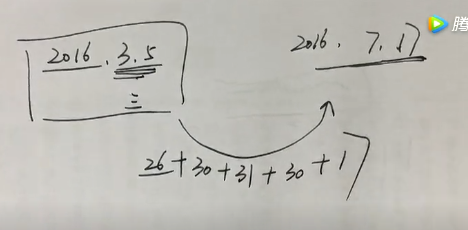
【例4】根据国务院办公厅部分节假日安排的通知,某年8月份有22个工作日,那么当年的8月1日可能是( )。
A.周一或周三
B.周三或周日
C.周一或周四
D.周四或周日
【作业A1】甲、乙、丙、丁四个人去图书馆借书,甲每隔5天去一次,乙每隔11天去一次,丙每隔17天去一次,丁每隔29天去一次,如果5月18日他们四个人在图书馆相遇,问下一次四个人在图书馆相遇是几月几号?( )
A.10月18日
B.10月14日
C.11月18日
D.11月14日
(13+31+30+31+31+30+31+x)
【作业A2】从A市到B市的航班每周一、二、三、五各发一班。某年2月最后一天是星期三。问当年从A市到B市的最后一次航班是星期几出发的?( )
A.星期一
B.星期二
C.星期三
D.星期五

余数同余(完整版)
余同取余,
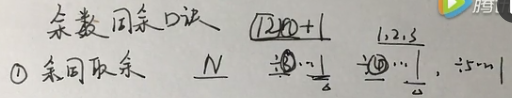
合同加和,
n/3..2 n/4..1 发现3+2=4+1 合同,因此就是12n+5

差同减差。

最小公倍数作周期。
识别特征:①除以几余几,除以几余几;或者②平均分成几组,剩几个或者差几个,平均分成几组,剩几个或者差几个。
例如 n/3..1 n/4..1 因此有 (原数 = 12n+1)
例如 n/3..1 n/4..1 n/5..2 因此先做前两个,12n+1 用这个去试下n/5,看看余数是不是2,然后得出第一项是37=12*3+1
三个人的公倍数 3 4 5 = 60
因此有 原数= 60n+37
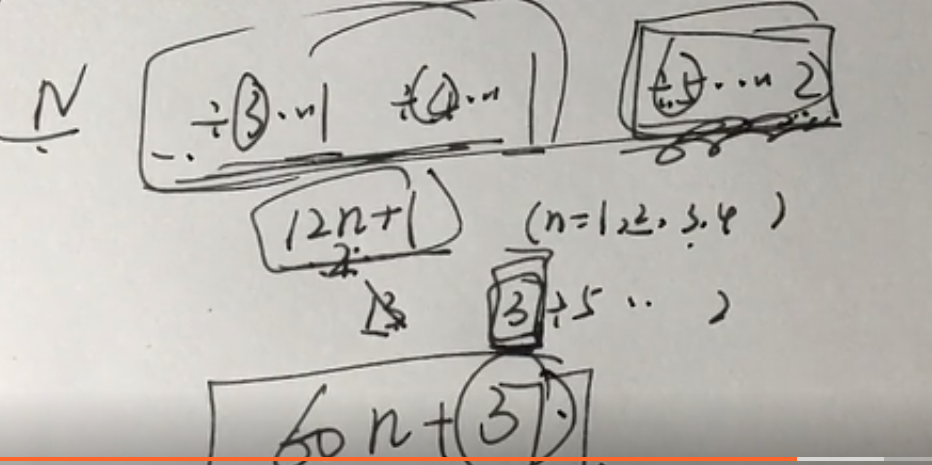
【作业A1】三位数的自然数P满足:除以7余2,除以6余2,余以5也余2,则符合条件的自然数P有( )。
A.2个
B.3个
C.4个
D.5个

【作业A2】一个小于200的数,它除以11余8,除以13余10,那么这个数是多少?( )
A.118
B.140
C.153
D.162

【作业B1】(2018浙江)某次比赛报名参赛者有213人,但实际参赛人数不足200。主办方安排车辆时,每5人坐一辆车,最后多2人;安排就餐时,每8人坐一桌,最后多7人;分组比赛时,每7人一组,最后多6人。问未参赛人数占报名人数的比重在以下哪个范围内?( )
A.低于20%
B.20%~25%之间
C.25%~30%之间
D.高于30%
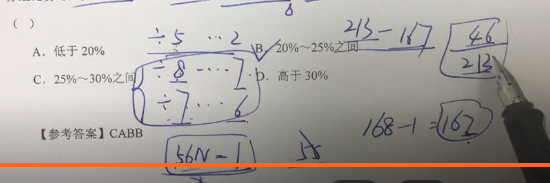
(这里后两项是差同,所以我们可以通过后两项来初步定总人数)得到56N-1,然后再一个个尝试,最后得到符合第一项的/5..2
牛吃草问题(边用边减少问题)
识别方式:“边吃边长(减少)”
识别方式2:已知条件读起来朗朗上口,一组排比句,NTNT(几头牛吃几天,几头牛吃几天)
常见类型:吃草、抽水、吃人(排队检票售票)、资源开采、上下扶梯等
核心公式:y=(N-x)×T
N:数量(牛)
T:时间
y:原有量
x:每单位时间的新增量(增长速度)
【作业A1】有一个水池,池底不断有泉水涌出,且每小时涌出的水量相同。现要把水池里的水抽干,若用5台抽水机40小时可以抽完,若用10台抽水机15小时可以抽完。现在用14台抽水机,多少小时可以把水抽完?( )
A.10小时
B.9小时
C.8小时
D.7小时

【作业A2】某水库共有10个泄洪闸,当10个泄洪闸全部打开时,8小时可将水位由警戒水位降至安全水位;只打开6个泄洪闸时,这个过程为24个小时,如水库每小时的入库量稳定,问如果打开8个泄洪闸时,需要多少小时可将水位降至安全水位?( )
A.10
B.12
C.14
D.16

【作业A2】药厂使用电动研磨器将一批晒干的中药磨成药粉,厂长决定从上午10点开始,增加若干台手动研磨器进行辅助作业,他估算若增加2台,可在晚上8点完成,若增加8台,可在下午6点完成。问如果希望下午3点完成,需增加多少台手动研磨器?( )
A.20
B.24
C.26
D.32

【作业B1】由于连日暴雨,某水库水位急剧上升,逼近警戒水位。假设每天降雨量一致,若打开2个水闸放水,则3天后正好到达警戒水位;若打开3个水闸放水,则4天后正好到达警戒水位。气象台预报,大雨还将持续七天,流入水库的水量将比之前多20%。若不考虑水的蒸发、渗透和流失,则至少打开几个水闸,才能保证接下来的七天都不会到达警戒水位?( )
A.5
B.6
C.7
D.8

数量关系中的一笔画
笔记整理:
题干特征:给定图形,要求走完图形的每一条边,求最短
方法步骤:
①确定图形的奇点数
②连线
未指定起点时:通过连接图形中的已有线段,将奇点数降到2个(原图奇点数小于等于2则不用连线)。(连接的线段应尽量短)
指定起点时:若指定的起点为奇点,则连线方法同上;指定的起点为偶点时,则需要将奇点数降为0个。
③计算
计算原图形所有线段总长度+连接的线段的长度
【例1】(2014黑龙江)某公园的道路由如下所示的5个正六边形组成,每个六边形每条边的长度都是100米,保安员从道路上某一点出发巡视完所有的道路至少要走多少米?( )
A.2600
B.2800
C.3000
D.2300
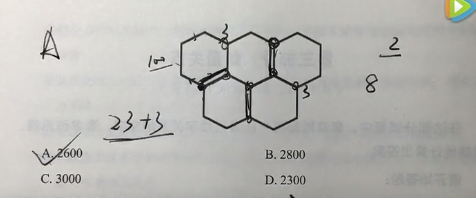
(一笔画问题,上面一共有八个奇点,那么我们用粗线段掩盖掉几个,剩下两个=可以一笔画)
(上面掩盖的三个可以重复走,要走多3段线段路程)
【作业A1】(2016山东)一块由两个正三角形拼成的菱形土地ABCD周长为800米,土地周围和中间的道路如下图所示,其中DE、BF分别与AB和CD垂直。 如要从该土地上任何一点出发走完每一段道路,问需要行进的距离最少是多少米?( )

植树方阵类专项练习
植树方阵类公式:
1.单边直线型:棵树=总长÷间隔+1
2.单边楼间型:棵树=总长÷间隔-1
3.环形植树公式:棵树=总长÷间隔
【例3】某条道路的一侧种植了25棵杨树,其中道路两端各种有一棵,且所有相邻的树距离相等。现在需要增种10棵树,且通过移动一部分树(不含首尾两棵)使所有相邻的树距离相等,则这25棵树中有多少棵不需要移动位置( )。
A.3
B.4
C.5
D.6
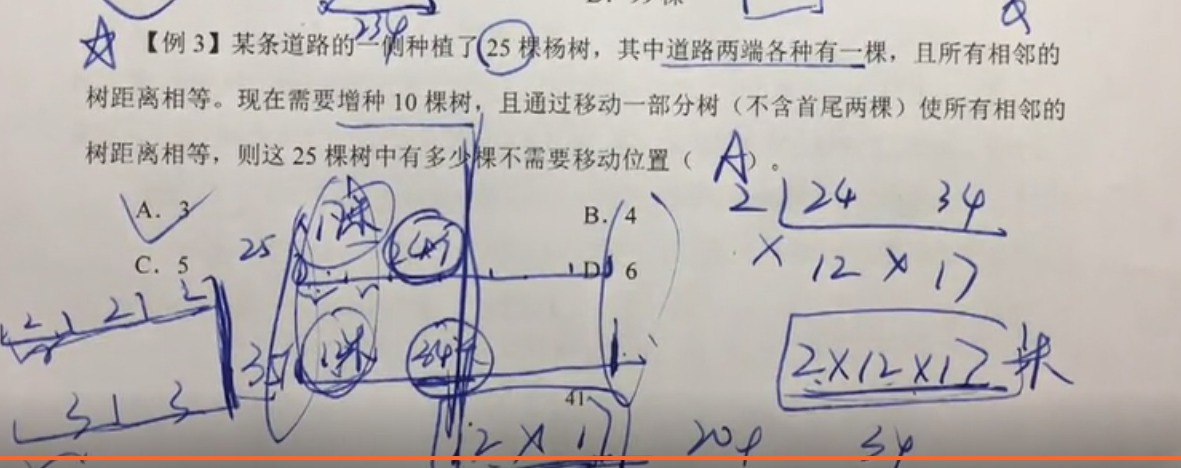
(这种题的方法就是找间隔的长度,假设分别是24和17,然后找公倍数--最小2*12*17,然后就算24和17在公倍数范围里面可以有多少个)
【作业A1】某单位两座办公楼之间有一条长204米的道路,在道路起点的两侧和终点的两侧已栽种了一棵树。现在要在这条路的两侧栽种更多的树,使每一侧每两棵树之间的间隔不多于12米。如栽种每棵树需要50元人工费,则为完成栽种工作,在人工费这一项至少需要做多少预算?( )
A.800
B.1600
C.1700
D.1800

【作业A2】某条道路进行灯光增亮工程,原来间隔35米的路灯一共有21盏,现要将路灯的间隔缩短为25米,那么有( )盏路灯无需移动。
A.2
B.3
C.4
D.5

(这里注意题目的坑点,有21个路灯,但是要包括前后的两个固定,所以中间只有19个路灯,就是分成20段)
方阵问题3个结论:
N阶方阵总人数N×N
最外层人数4N-4
相邻两圈相差8人
【作业A3】有一队士兵排成若干层的中空方阵,外层人数共有60人,中间一层共有44人,则该方阵士兵的总人数是( )。
A.156人
B.210人
C.220人
D.280人
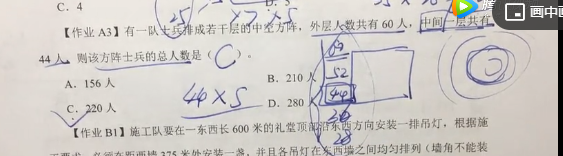
【作业B1】施工队要在一东西长600米的礼堂顶部沿东西方向安装一排吊灯,根据施工要求,必须在距西墙375米处安装一盏,并且各吊灯在东西墙之间均匀排列(墙角不能装灯)。该施工队至少需要安装多少盏吊灯?
A.6
B.7
C.8
D.9

(最大公约数)