直线生成算法

所谓图元的生成，是指完成图元的参数表示形式（由图形软件包的使用者指定）到点阵表示形式（光栅显示系统刷新时所需的表示形式）的转换。通常也称扫描转换图元。

直线的扫描转换：确定最佳逼近于该直线的一组像素，并且按扫描线顺序对这些像素进行写操作。

三个常用算法：1、数值微分法DDA；2、中点画线法；3、Bresenham算法。

生成目标，求与直线段充分接近的像素集

生成前提条件:1、像素网格均匀，坐标为整数值；2、直线段的宽度为1；3、直线段的斜率k的取值范围为[-1,1]。

1、数值微分法

1.1 基本思想

已知过端点P0 (x0, y0), P1(x1, y1)的直线段L: y=kx+b 直线斜率为

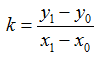，x从左端点x₀开始，向右端点x₁以步长=1(个象素)，计算相应的y坐标y=kx+b；取象素点(x, y(x))作为当前点的坐标。

计算y_i+1 = kx_i+1+b                                   

                   = k₁x_i+b+kDx

                   = y_i+kDx                            当Dx =1; y_i+1 = y_i+k 。

1.2 分析

• 当x每递增1，y递增k(即直线斜率)；
• 注意上述分析的算法仅适用于|k| ≤1的情形。在这种情况下，x每增加1,y最多增加1。
• 当 |k| >1时，必须把x，y位置互换
• 按照直线从（x0，y0）到（x1，y1）的方向不同，分为8个象限。对于方向在第1a象限内的直线而言， Dx=1， Dy=k。对于方向在第1b象限内的直线而言，取值Dy=1， Dx=1/k。

对应关系如下图所示：

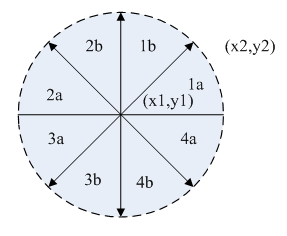
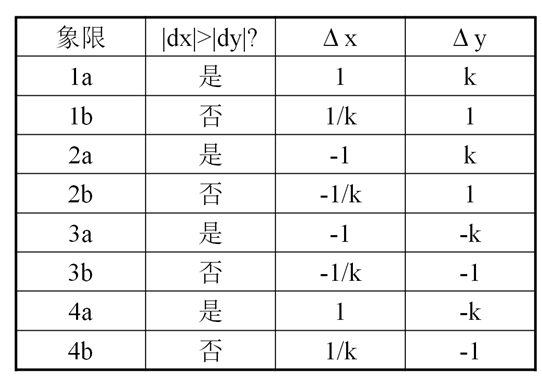
2、中点画线法

2.1 基本思想

当前像素点为p(x_p, y_p) ，下一个象素点为P1或P2。设M=(x_p+1, y_p+0.5)，为p₁与p₂的中点，Q为理想直线与x=x_p+1垂线的交点。将Q与M的y坐标进行比较。

如下图所示：

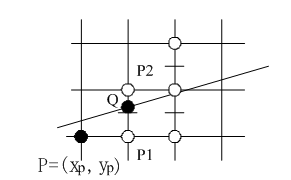
当M在Q的下方，则P₂应为下一个象素点；

当M在Q的上方，应取P₁为下一点。

2.2 分析

构造判别式:d=F(M)=F(x_p+1,y_p+0.5) = a(x_p+1)+b(y_p+0.5)+c

           其中a=y₀-y₁, b=x₁-x₀, c=x₀y₁-x₁y₀

当d<0，M在L（Q点）下方，取右上上方P_U为下一个像素；

当d>0，M在L(Q点)上方，取右方P_D为下一个像素；

当d=0，选P₁或P₂均可，约定取P_D为下一个像素；

d是x_p, y_p的线性函数，因此可采用增量计算，提高运算效率。初值d₀=F(x₀+1, y₀+0.5)=a+0.5b。

(1) 若当前象素处于d>=0情况，则取正右方像素P_D（x_p+1, y_p）, 要判下一个像素位置，应计算：d_i+1=F(x_p+2, y_p+0.5)=a(x_p+2)+b(y_p+0.5)=d+a； 增量为a。

(2) 若d<0时，则取右上方像素P_U（x_p+1, y_p+1）。要判断再下一像素，则要计算：d_i+1= F(x_p+2, y_p+1.5)=a(x_p+2)+b(y_p+1.5)+c=d+a+b ；增量为a＋b。

画线从(x₀, y₀)开始，d的初值

                    d₀=F(x₀+1, y₀+0.5)=F(x₀, y₀)+a+0.5b =a+0.5b。

可以用2d代替d来摆脱小数，提高效率。

 2.3 实例演示

用中点画线法画出P0(0,0) ,P1(5,2)的直线。

首先构造出判别式：d = a(x_p+1)+b(y_p+0.5)+c 。其中a = y0 - y1 = -2，b = x1 - x0 = 5，c = x0y1 - x1y0 = 0。

则初值d0 = a + 0.5b = 0.5。取点P'(1,0)为下一个像素的位置。按照规则(1)、(2)计算，可以得到下列结果表：

i	xi	yi	d
1	0	0	0.5
2	1	0	-1.5
3	2	1	1.5
4	3	1	-0.5
5	4	2	2.5

用坐标表示，下图：

3、Bresenham算法

3.1 基本思想

过各行各列象素中心构造一组虚拟网格线。按直线从起点到终点的顺序计算直线与各垂直网格线的交点，然后根据误差项的符号确定该列象素中与此交点最近的象素。

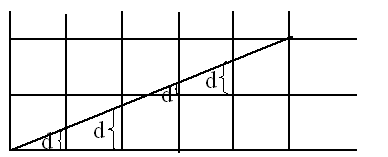
3.2 分析

设直线方程为：    ，其中k=dy/dx。 因为直线的起始点在象素中心，所以误差项d的初值d0＝0。

x下标每增加1，d的值相应递增直线的斜率值k，即d＝d＋k。一旦d≥1，就把它减去1，这样保证d在0、1之间。

当d≥0.5时，最接近于当前象素的右上方象素（xi＋1，yi＋1）

当d<0.5时，更接近于右方象素（xi＋1，yi）。

为方便计算，令e＝d-0.5，e的初值为-0.5，增量为k。

当e≥0时，取当前象素（xi，yi）的右上方象素（xi＋1，yi＋1）；

当e<0时，更接近于右方象素（xi＋1，yi）。

3.3 实例演示

用Bresenham算法画出P0(0,0) ,P1(5,2)的直线。

计算得出斜率k = dy/dx = 0.4。

结果如下表：

i	x	y	e
1	0	0	-0.5
2	1	0	-0.1
3	2	1	0.3
4	3	1	-0.3
5	4	2	0.1
6	5	2	-0.5

坐标表示：

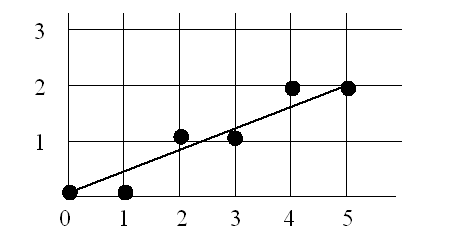
上述Bresenham算法在计算直线斜率与误差项时用到小数与除法。可以改用整数以避免除法。由于算法中只用到误差项的符号，因此可作如下替换

         这样e’的初值是-dx，由于k=dy/dx，所以e’的增量就变为2*dy。

3.4 Bresenham算法的优点

• 不必计算直线斜率，因此不做除法；
• 不用浮点数，只用整数；
• 只做整数加减法和乘2运算，而乘2运算可以用硬件移位实现。
• Bresenham算法速度很快，并适于用硬件实现。