#include <iostream>
#include <stdio.h>
#include <cstdlib>
#include <cstring>
#include <string>
#include <queue>
using namespace std;
typedef struct MGraph{
string vexs[10];//顶点向量
int arcs[10][10];//邻接矩阵
int vexnum, arcnum;//图的顶点数和边数
}MGraph;
int LocateVex(MGraph G, string u)//返回顶点u在图中位置
{
for(int i=0; i<G.vexnum; i++)
if(u==G.vexs[i])
return i;
return -1;
}
void CreateUDG(MGraph &G)//构造无向图
{
string v1,v2;
int i, j, k;
cout<<"请输入顶点数和边数:";
cin>>G.vexnum>>G.arcnum;
cout<<"请输入顶点:";
for(i=0; i<G.vexnum; i++)
cin>>G.vexs[i];
for(i=0; i<G.vexnum; i++)
for(j=0; j<G.vexnum; j++)
G.arcs[i][j]=0;
cout<<"请输入边:"<<endl;
for(k=0; k<G.arcnum; k++)
{
cin>>v1>>v2;
i=LocateVex(G, v1);
j=LocateVex(G, v2);
G.arcs[i][j]=G.arcs[j][i]=1;
}
}
void CreateUDN(MGraph &G)//构造无向网
{
string v1, v2;
int i, j, k;
int w;
cout<<"请输入顶点数和边数:";
cin>>G.vexnum>>G.arcnum;
cout<<"请输入顶点:";
for(i=0; i<G.vexnum; i++)
cin>>G.vexs[i];
for(i=0; i<G.vexnum; i++)
for(j=0; j<G.vexnum; j++)
G.arcs[i][j]=-1000;
cout<<"请输入边:"<<endl;
for(k=0; k<G.arcnum; k++)
{
cin>>v1>>v2>>w;
i=LocateVex(G, v1);
j=LocateVex(G, v2);
G.arcs[i][j]=G.arcs[j][i]=w;
}
}
void CreateDG(MGraph &G)//构造有向图
{
string v1, v2;
int i, j, k;
cout<<"请输入顶点数和边数:";
cin>>G.vexnum>>G.arcnum;
cout<<"请输入顶点:";
for(i=0; i<G.vexnum; i++)
cin>>G.vexs[i];
for(i=0; i<G.vexnum; i++)
for(j=0; j<G.vexnum; j++)
G.arcs[i][j]=0;
cout<<"请输入边:"<<endl;
for(k=0; k<G.arcnum; k++)
{
cin>>v1>>v2;
i=LocateVex(G, v1);
j=LocateVex(G, v2);
G.arcs[i][j]=1;
}
}
void CreateDN(MGraph &G)//构造有向网
{
string v1, v2;
int i, j, k;
int w;
cout<<"请输入顶点数和边数:";
cin>>G.vexnum>>G.arcnum;
cout<<"请输入顶点:";
for(i=0; i<G.vexnum; i++)
cin>>G.vexs[i];
for(i=0; i<G.vexnum; i++)
for(j=0; j<G.vexnum; j++)
G.arcs[i][j]=-1000;
cout<<"请输入边:"<<endl;
for(k=0; k<G.arcnum; k++)
{
cin>>v1>>v2>>w;
i=LocateVex(G, v1);
j=LocateVex(G, v2);
G.arcs[i][j]=w;
}
}
int FirstAdjVex(MGraph G, int v)//返回顶点v的第一个邻接顶点序号
{
for(int i=0; i<G.vexnum; i++)
if(G.arcs[v][i]==1)
return i;
return -1;
}
int NextAdjVex(MGraph G, int v, int w)//返回顶点v的相对于w的下一个邻接顶点序号
{
for(int i=w+1; i<G.vexnum; i++)
if(G.arcs[v][i]==1)
return i;
return -1;
}
bool visited[100];
void DFS(MGraph G, int v)
{
visited[v]=true;
cout<<G.vexs[v]<<" ";
for(int w=FirstAdjVex(G, v); w>=0; w=NextAdjVex(G, v, w))
if(!visited[w])
DFS(G, w);
}
void DFSTraverse(MGraph G)//深搜
{
for(int i=0; i<G.vexnum; i++)
visited[i]=false;
for(i=0; i<G.vexnum; i++)
if(!visited[i])
DFS(G, i);
}
void BFSTraverse(MGraph G)//广搜,类似于树的层次遍历
{
for(int i=0; i<G.vexnum; i++)
visited[i]=false;
queue<int> q;
for(i=0; i<G.vexnum; i++)
{
if(!visited[i])
{
visited[i]=true;
q.push(i);
while(!q.empty())
{
int v=q.front();
q.pop();
cout<<G.vexs[v]<<" ";
for(int w=FirstAdjVex(G, v); w>=0; w=NextAdjVex(G, v, w))
{
if(!visited[w])
{
visited[w]=true;
q.push(w);
}
}
}
}
}
}
void main()
{
MGraph g;
CreateUDG(g);
cout<<"深搜:";
DFSTraverse(g);
cout<<endl;
cout<<"广搜:";
BFSTraverse(g);
cout<<endl;
}
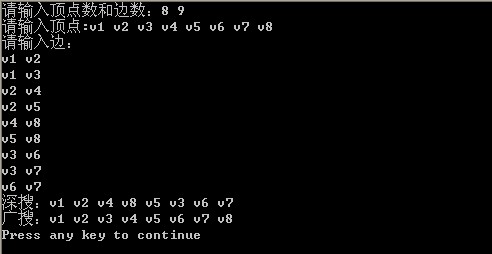
图的结构如下: